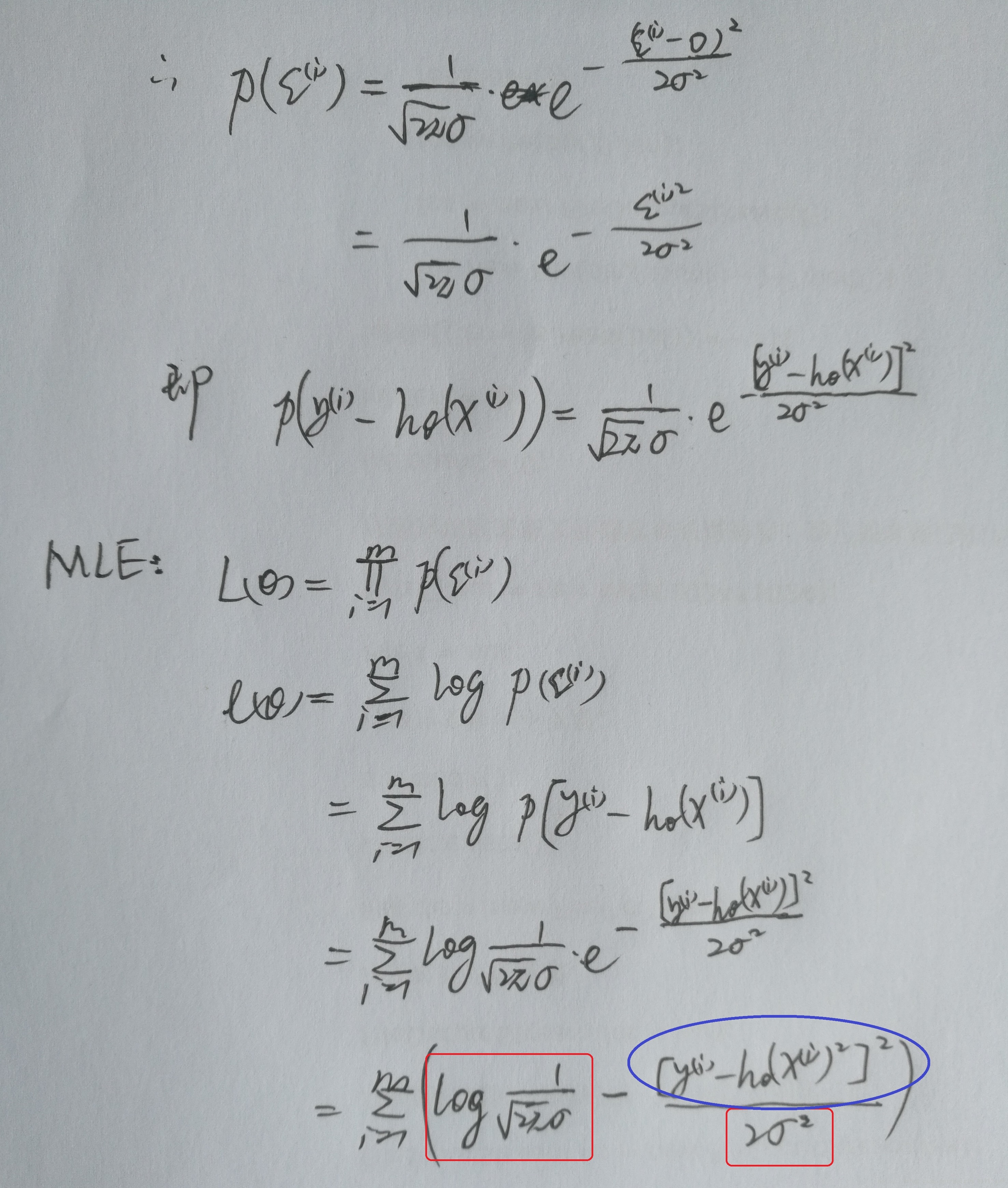【机器学习经典算法梳理】是一个专门梳理几大经典机器学习算法的博客。我在这个系列博客中,争取用最简练的语言、较简洁的数学公式,和清晰成体系的提纲,来尽我所能,对于算法进行详尽的梳理。【机器学习经典算法梳理】系列博客对于机器学习算法的梳理,将从“基本思想”、“基本形式”、“过程推导”、“损失函数”、“sklearn库的参数含义”和“总结”几个方面去进行。下面,就让我开始第一个算法,线性回归吧!
一.线性回归的基本思想:
插一句话:我将尽量都从【“你是谁?”(本质)、“从哪来?”(问题定位及目标)和“到哪去”(解决方法)】三个方面,对一件事物进行阐述。原因无他,就是为了清晰、易记、不容易漏知识点。
1.从本质来说,线性回归分属“回归”问题,即linear regression预测的结果是连续值;
2.从定位上说,线性回归是广义线性回归的一员(又称指数族分布Exponential Family)。线性回归的目标,即寻找一条直线。使所有样本点到这条直线的距离之和最小;
3.从该算法的解决方法来说,线性回归对输入(input)进来的各个特征(features)乘上不同的权重,然后相加得到一条直线(一元线性回归)或超平面(多元)。我们利用“最小二乘法”,使得各个样本点到这条直线的距离最小,最终得到这个“权重”。
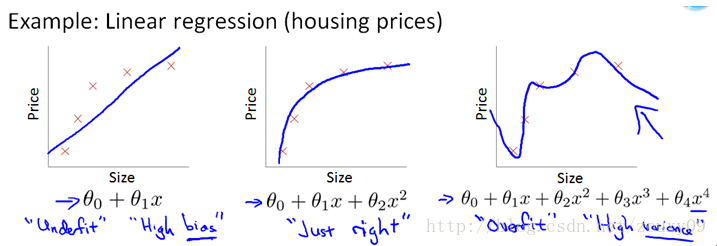
4.值得一提的是,所谓“线性回归”并非意味着所有feature都得是1次的,它意味着,当你将每种特征组合都分配一个维度的时候(向高维映射),所得到的回归结果是一条直线(超平面)。如下图,你在二维坐标系上表示一元特征的线性回归,那么得到的是直线;但对于多元线性回归而言(如最右边),只有当你在5维空间去描述的时候,才可以得到一个超平面。
二.线性回归的基本形式:
$$h_{\theta}(x) = X\Theta$$
其中,\(h_{\theta}(x)\)表示对真实值y的预测。
三.推导过程与损失函数:
设真实值为\(y^{(i)}\),线性回归算法值为\(h_{\theta}(x^{(i)})\),很明显,二者之间应该存在误差,这种误差可能是因为未考虑进来的变量、噪声等因素导致的,根据大数定律,这个误差应该服从正态分布,我们在这里将预测与真实值之间的误差记作\(\epsilon ^{(i)}\),则有:$$y^{(i)} = h_{\theta}(x^{(i)}) + \epsilon^{(i)}$$
且有:$$\epsilon ^{(i)} \sim N(0,\sigma ^{2}) $$
下面以图片形式附上推导过程:
由上面的对数似然函数\(l(\theta)\)和最大似然估计(MLE)性质可知,两个红框内为定值、只有蓝框内是变化的,因而若想使\(l(\theta)\)取到最大值,则需要让蓝框内的表达式取到最小。因而我们的损失目标函数即:
$$loss(\theta) = \sum_{i=1}^{m}\left [y ^{(i)} - h_{\theta}(x^{(i)}) \right ]^{2}$$
找到最佳,让loss(\(\theta)\)取最大值,因而对损失函数loss(
)求导并令导数为零,得到\(\Theta\)解析解:$$(X^{T}X)^{-1}X^{T}\overrightarrow{y}$$
四.Ridge、Lasso与正则约束:
我们常见的正则约束主要有两种——L1-norm,L2-norm,其实还有个L0-norm。
1.L0范数:
L0范数指的是全部非零元素的个数。可见L0范数可以达到使特征稀疏的效果。而使得特征变得稀疏,是非常有意义的,这种意义体现在以下两点:
(1)一方面,这样增强了模型的可解释性——在你手里有一份模型预测所得的结果,当你发现,有200个特征影响着这个结果的时候,你会觉得无比头大,难以解释每个特征对结果的影响;但当你使特征变得稀疏,只有5个特征非零时,你就可以很轻松地搞清结果如何受这5个特征的影响;
(2)另一方面,稀疏约束可以完成对特征的选择——我们得到的原始数据中,有许多特征都对结果影响甚微,甚至根本就没有影响。这些特征信息的存在,导致模型可以在训练集上学到这些“噪声”,从而或许会对训练集的误差减小有帮助;然而在测试集上进行预测时,这些无用的特征反而被考虑进去,反而干扰了结果预测。
然而,L0范数甚至只是一个定义,我们难以去直接将L0范数加入损失函数中进行求导等计算。同时我们发现L1范数同样可以使特征达到稀疏的效果,所以我们在“稀疏约束”的实际运用中其实被大量应用的,是L1范数。
2.L1范数与LASSO:
L1范数基本形式:$$\left \| \theta \right \|_{1} = \sum_{i}\left | \theta_{i} \right |$$
由前已知,L1范数是稀疏约束,那么将L1范数和线性回归损失函数联系起来,就可以在利用最小二乘法找到“最优直线”的同时,将许多不重要的特征权重置为0:$$Loss = \sum_{i=1}^{m}\left [y ^{(i)} - h_{\theta}(x^{(i)}) \right ]^{2}s.t. \sum_{i=1}^{m}\left | \theta \right | \leq C$$
应用拉格朗日乘子法,引入拉格朗日乘子\(\lambda\),我们可将有约束的最小化Loss问题转化成无约束的最小化Loss问题:$$Lasso Loss = \sum_{i=1}^{m}\left [y ^{(i)} - h_{\theta}(x^{(i)}) \right ]^{2}+\lambda\sum_{i=1}^{m}\left | \theta_{i} \right |$$
在这里,将L1范数称作损失函数的“正则项”,称作L1正则,就是对模型参数的一种约束,或曰——惩罚。而采取了L1正则的线性回归,又称“LASSO”。式中的\(\lambda\)作为一个权衡因子,权衡着L1正则项对于损失函数的惩罚力度。至于为何L1正则可以使特征变得稀疏,将在L2正则之后一并探讨。
3.L2范数与Ridge:
L2范数基本形式:$$\left \| \theta \right \|_{2} = \sum_{i} \left (\theta_{i}^{2} \right )^{1/2}$$
L2范数介绍:如上面的公式,L2范数就是全部模型参数(即各特征权重)的平方和。L2范数可以通过对过大的模型参数\(\theta\)的惩罚,使得模型相对简单、各参数(权重)取值较小,得到一个较简单的模型,从而有效降低过拟合的情况。那么为什么减小各模型参数、使模型更简单就可以减小过拟合了呢?
依我所见,由于L2范数作为线性回归损失函数的正则项,是全体模型参数\(\theta\)的平方之和,所以参数\(\theta\)自然是越小越好;而损失函数的第一项,即每个样本点的误差平方和,会随着模型参数\(\theta\)的增大而减小,因而参数\(\theta\)自然是越大越好,但自然也会导致过拟合。那么在加入L2正则、衰减某些特征的权重时就涉及到“衰减哪些特征权重”的问题。对于重要的特征,如果被L2正则衰减了权重,则会导致损失函数第一项(每个样本点的误差平方和)急速增长,而该权重的衰减对损失函数最小化的贡献就显得微不足道了;相反,如果是不重要的特征,其权重衰减对于损失函数第一项没什么影响,同时还会使损失函数第二项——L2正则项减小,则对损失函数最小化是有贡献的。因而L2正则项的加入会衰减不重要的特征的权重,而一旦不重要的特征被模型习得,就会导致过拟合。从这点来说,L2对不重要特征的权重进行衰减,自然是有助于模型避免过拟合喽!
加了L2正则项的线性回归:$$Loss = \sum_{i=1}^{m}\left [y ^{(i)} - h_{\theta}(x^{(i)}) \right ]^{2} s.t.\sum_{i} \theta_{i}^{2} \leq C$$
同上,使用拉格朗日乘子法,引入“权衡因子”\(\lambda\),可得下式(引入L2正则的线性回归称为Ridge回归):
$$Ridge Loss =\sum_{i=1}^{m}\left [y^{(i)}-h_{\theta}(x^{(i)}) \right ]^{2} +\lambda \sum_{i} \theta_{i}^{2}$$
L2正则会使各特征的权重衰减,尤其是重要性较低的特征的权重,然而却并不会使某一权重衰减成0,最多只会接近0,因而L2正则不是“稀疏约束”。至于原因?马上道来——
4.L1正则可使特征稀疏、L2正则可衰减特征权重的原因:
$$Lasso : \mathop{\arg\min}_{\theta} \left (\sum_{i=1}^{m}\left [y ^{(i)} - h_{\theta}(x^{(i)}) \right ]^{2} \right )s.t.\sum_{i=1}^{m}\left | \theta \right | \leq C$$
$$Ridge : \mathop{\arg\min}_{\theta} \left (\sum_{i=1}^{m}\left [y ^{(i)} - h_{\theta}(x^{(i)}) \right ]^{2} \right )s.t.\sum_{i} \theta_{i}^{2} \leq C$$
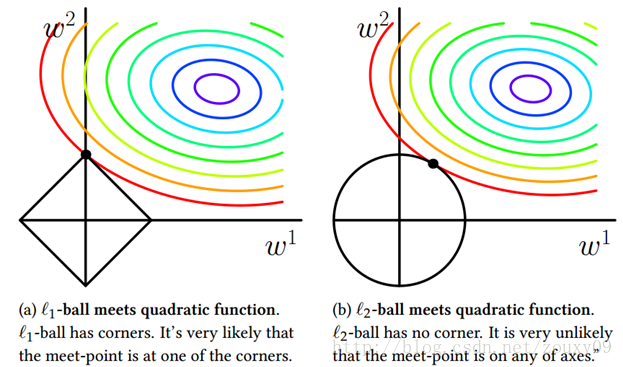
如图所示,我们假设该模型中只有两个参数,然后根据带有约束的Lasso和Ridge的损失函数绘制出了两张图。彩色线为二者相同的第一项——误差平方和的最优解等高线(由于是二次函数,所以是凸的)。 L1正则项由于是绝对值不等式约束,故取值在一个菱形内部;L2正则项由于是二次不等式约束,因而取值在一个圆内。
可见,L1-ball 与L2-ball 的最大的区别就是,L1-ball在坐标轴上是一个“尖”,也就是说在坐标轴处不可微;L2-ball处处圆滑。所以除非等高线位置非常赶巧,否则等高线与L1-ball的第一次相交基本都在坐标轴的尖上。如上面左图,等高线交L1-ball于w2轴,这就意味着w1=0,L1正则的稀疏效应显现出来了。
相比之下,L2-ball 就没有这样的性质。因为L2-ball处处圆滑,所以等高线交L2-ball于坐标轴之上的可能性就小很多,因而L2不具备稀疏性。
五.sklearn库的参数含义:
| 参数 | 解释 |
|---|---|
| alpha:float | 正则项力度,即“权衡因子”\(\lambda\)。 在SVC、LogisticRegression或LinearSVC中,C就是alpha的倒数 可以传入一个list,这个list的shape必须和特征数目相同,以指定每个特征的“惩罚力度”。 |
| fit_intercept : boolean | 默认为True,意思是拟合数据的偏度。若设为False,则应该提前对数据进行处理,将其“中心化” 关于数据中心化,即“标准化(Standardization)”,详见数据的归一化、标准化 |
| tol : float | 结束迭代时,结果的精度。 |
| 属性 | 解释 |
|---|---|
| coef_ | 权重向量(所有模型参数) |
| intercept_ | 结果里面的截距项 |
Lasso和Ridge类似,但Lasso的属性中多了一个sparse_coef_属性,该属性的输出值为scipy.sparse matrix,即稀疏矩阵。具体使用,请参照https://www.jianshu.com/p/1177a0bcb306
打字辛苦,码字不易,若转载请注明出处,欢迎大家共同讨论,谢谢!