方程组若干概念
n元齐次线性方程组
n元非齐次线性方程组
n元齐次线性方程组 (所有xi都为0一定是方程的解)
矩阵的若干概念
m*n个数的数表
任意一个数称之为元素
全为实数的称为实矩阵,存在复数的称之为复矩阵
行数和列数相等的称之为方阵
只有一行的矩阵称之为行矩阵又称之为行向量
只有一列的矩阵称之为列矩阵又称之为列向量
两个矩阵的行数和列数相等称之为同型矩阵
同型矩阵对应的元素相等记作A=B
系数矩阵 未知矩阵 常数项矩阵 增广矩阵
除对角线外,的都是0称之为对角矩阵
对角矩阵对角线上的值都为1,称之为单位阵。
矩阵的运算
1 矩阵的加法
只有同型矩阵才可以运算
A+B=B+A
A+(B+C) = A+B+C
2 数与矩阵相乘
(
λ
μ )A =
λ(
μA)
(
λ+
μ )A =
λA+
μA
λ(A+B) =
λA+
λB
3 矩阵与矩阵相乘
满足结合律和分配率
(AB)C = A(BC)
(
λ)AB = (
λA)B
A(B+C) = AB+AC
矩阵的转置
(AT)T = A
(A+B)T =
AT+
BT
(λA)T =
λ
AT
(AB)T =
BTAT
∣A∣T=∣A∣
方针的行列式
由方针构成的行列式
∣AT∣ =
∣A∣
∣λA∣ =
λn∣A∣
|AB| =
∣A∣∣B∣
伴随矩阵
行列式每个位置由代数余子式构成的矩阵转置称之为伴随矩阵
AA∗ =
A∗A = |A|E
(a∗)∗ =
∣A∣n−2
(kA)∗=kn−1A∗
(AB)∗ =
B∗A∗
∣A∗∣=∣A∣n−1
伴随矩阵求法定义法 公式法
|A|!=0 即A可逆
A∗=∣A∣A−1
逆矩阵
定义 如果对于一个矩阵由AB=BA=E则称A是可逆的,B为A的逆矩阵
唯一: 逆矩阵存在唯一
定理1: 矩阵A可逆,则|A| != 0
定理2:
A−1 =
∣A∣A∗
AB = E 推出 B =
A−1
推论1:A 可逆
A−1亦可逆
(A−1)−1=A
推论2:
(λA)−1 =
λ1A−1
推论3:A,B可逆 AB亦可逆
(AB)−1=B−1A−1
推论4:|
A−1| =
∣A∣−1
求法:
1 用定义
2 用伴随
3 用初等变换
公式对比
| 转置 |
伴随 |
逆 |
|
(AT)T = A |
(a∗)∗ =
∥a∥n−2 |
(A−1)−1=A |
|
(λA)T =
λ
AT |
(kA)∗=kn−1A∗ |
(λA)−1 =
λ1A−1 |
|
(AB)T =
BTAT |
(AB)∗ =
B∗A∗ |
(AB)−1=B−1A−1 |
|
∥A∥T=∥AT∥ |
∥A∗∥=∥A∥n−1 |
∥A∥−1=∥A−1∥ |
|
(A+B)T =
AT+
BT |
无 |
无 |
克拉默法则的推广
A = 系数矩阵
Aj = 1到j-1列 并 b 并 j+1 到 n
分块矩阵
分块矩阵的性质与普通矩阵类似
可理解为广义矩阵
扫描二维码关注公众号,回复:
5981011 查看本文章

对角分块矩阵
反对角矩阵
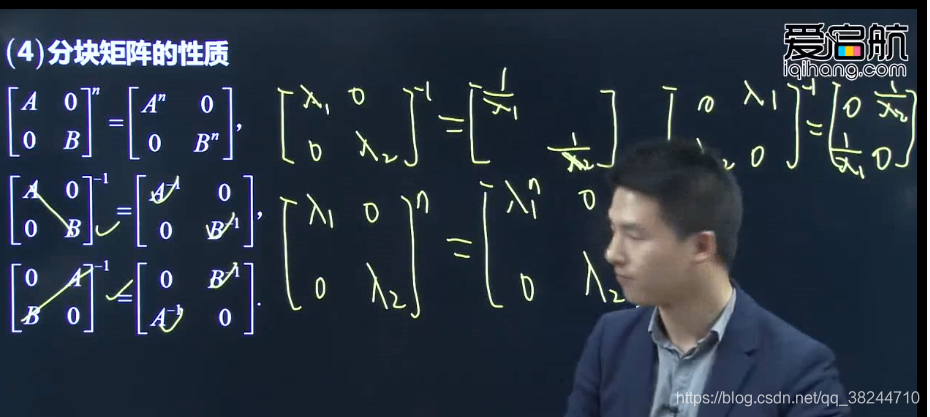 附加:证明矩阵A=O 即证明
ATA=O
附加:证明矩阵A=O 即证明
ATA=O
AB != BA
(A+B)2!=A2+B2+2AB
A2−B2!=(A−B)(A+B)
A2=0 不能推出A=0
A2=A 不能推出A=0或者A=E
AX=AY 且A!=0 不能推出X=Y

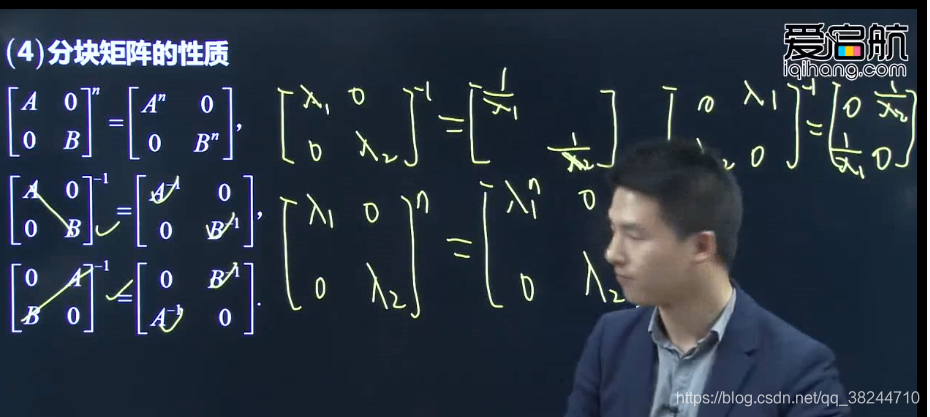 附加:证明矩阵A=O 即证明
附加:证明矩阵A=O 即证明