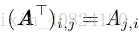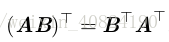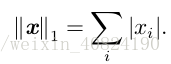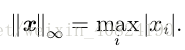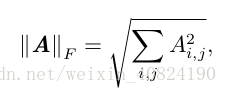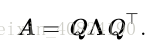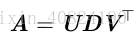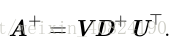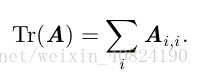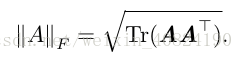第二章-线性代数
2.1 标量、向量、矩阵和张量
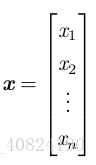
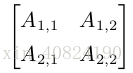
张量(tensor):在某些情况下,我们会讨论坐标超过两维的数组。一般地,一个数组中的元素分布在若干维坐标的规则网格中,我们称之为张量。我们使用字体 A 来表示张量 “A’’。张量 A 中坐标为 (i, j, k) 的元素记作 A i,j,k。
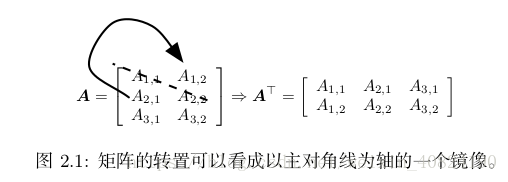
转置(transpose):
2.2 矩阵和向量相乘
C = AB:如果矩阵 A 的形状是 m × n,矩阵 B 的形状是 n × p,那么矩阵C 的形状是 m × p。
矩阵乘积服从分配律:A(B + C) = AB + AC
矩阵乘积也服从结合律:A(BC) = (AB)
不同于标量乘积,矩阵乘积并不满足交换律(AB = BA 的情况并非总是满足)。
矩阵乘积的转置:
两个向量的点积(dot product)满足交换律:
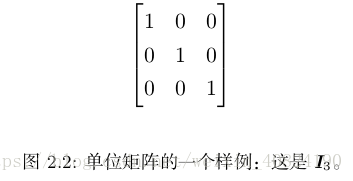
2.3 单位矩阵和逆矩阵
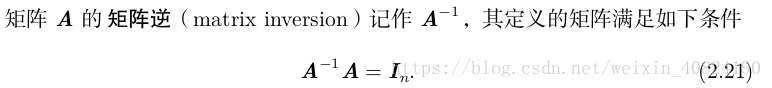
2.4 线性相关和生成子空间(p32)
2.5 范数
有时我们需要衡量一个向量的大小。在机器学习中,我们经常使用被称为 范数(norm)的函数衡量向量大小。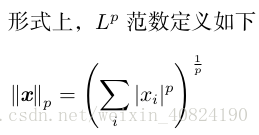
范数是将向量映射到非负值的函数。直观上来说,向量 x 的范数衡量从原点到点 x 的距离。
当 p = 2 时,L2范数被称为 欧几里得范数(Euclidean norm)。它表示从原点出发到向量 x 确定的点的欧几里得距离。L2范数在机器学习中出现地十分频繁,经常简化表示为||x||略去了下标 2。平方L2 范数也经常用来衡量向量的大小,可以简单地通过点积xTx 计算。
注意:平方 L2 范数在数学和计算上都比 L2 范数本身更方便。例如,平方 L2 范数对x 中每个元素的导数只取决于对应的元素,而 L2 范数对每个元素的导数却和整个向量相关。但是在很多情况下,平方 L2 范数也可能不受欢迎,因为它在原点附近增长得十分缓慢。在某些机器学习应用中,区分恰好是零的元素和非零但值很小的元素是很重要的。在这些情况下,我们转而使用在各个位置斜率相同,同时保持简单的数学形式的函数:L1 范数。L1 范数可以简化如下:
当机器学习问题中零和非零元素之间的差异非常重要时,通常会使用 L1 范数。每当x 中某个元素从 0 增加 ε,对应的 L 1 范数也会增加 ε。
另外一个经常在机器学习中出现的范数是 L ∞ 范数,也被称为 最大范数(max norm)。这个范数表示向量中具有最大幅值的元素的绝对值:
有时候我们可能也希望衡量矩阵的大小。在深度学习中,最常见的做法是使用 Frobenius 范数(Frobenius norm),F-范数。
2.6 特殊类型的矩阵和向量
2.7 特征分解
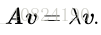
每个实对称矩阵都可以分解成实特征向量和实特征值:
2.8 奇异值分解
奇异值分解(singular value decomposition, SVD),将矩阵分解为奇异向量(singular vector)和 奇异值(singular value)。通过奇异值分解,我们会得到一些与特征分解相同类型的信息。然而,奇异值分解有更广泛的应用。每个实数矩阵都有一个奇异值分解,但不一定都有特征分解。例如,非方阵的矩阵没有特征分解,这时我们只能使用奇异值分解。
假设 A 是一个 m × n 的矩阵,那么 U 是一个 m × m 的矩阵,D 是一个 m × n的矩阵,V 是一个 n × n 矩阵。这些矩阵中的每一个经定义后都拥有特殊的结构。矩阵 U 和 V 都定义为正交矩阵,而矩阵 D 定义为对角矩阵。注意,矩阵 D 不一定是方阵。
对角矩阵 D 对角线上的元素被称为矩阵 A 的奇异值(singular value)。矩阵U 的列向量被称为左奇异向量(left singular vector),矩阵 V 的列向量被称 右奇异向量(right singular vector)。
事实上,我们可以用与 A 相关的特征分解去解释 A 的奇异值分解。A 的 左奇异向量(left singular vector)是 AAT 的特征向量。 A 的 右奇异向量(right singularvector)是ATA的特征向量。A 的非零奇异值是ATA特征值的平方根,同时也是AAT 特征值的平方根。
2.9 Moore-Penrose 伪逆
对于非方矩阵而言,其逆矩阵没有定义。Moore-Penrose 伪逆(Moore-Penrose pseudoinverse)使我们在这类问题上取得了一定的进展。矩阵 A 的伪逆定义为:
计算伪逆的实际算法没有基于这个定义,而是使用下面的公式:
2.10 迹运算
用迹运算表示表达式,我们可以使用很多有用的等式巧妙地处理表达式。例如,迹运算在转置运算下是不变的:
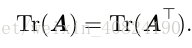
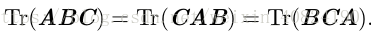
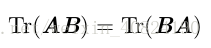
另一个有用的事实是标量在迹运算后仍然是它自己:a = Tr(a)。
2.11 行列式
第二章-线性代数
2.1 标量、向量、矩阵和张量
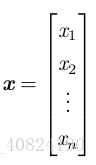
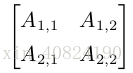
张量(tensor):在某些情况下,我们会讨论坐标超过两维的数组。一般地,一个数组中的元素分布在若干维坐标的规则网格中,我们称之为张量。我们使用字体 A 来表示张量 “A’’。张量 A 中坐标为 (i, j, k) 的元素记作 A i,j,k。
转置(transpose):
2.2 矩阵和向量相乘
C = AB:如果矩阵 A 的形状是 m × n,矩阵 B 的形状是 n × p,那么矩阵C 的形状是 m × p。
矩阵乘积服从分配律:A(B + C) = AB + AC
矩阵乘积也服从结合律:A(BC) = (AB)
不同于标量乘积,矩阵乘积并不满足交换律(AB = BA 的情况并非总是满足)。
矩阵乘积的转置:
两个向量的点积(dot product)满足交换律:
2.3 单位矩阵和逆矩阵

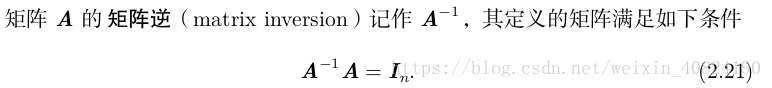
2.4 线性相关和生成子空间(p32)
2.5 范数
有时我们需要衡量一个向量的大小。在机器学习中,我们经常使用被称为 范数(norm)的函数衡量向量大小。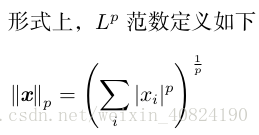
范数是将向量映射到非负值的函数。直观上来说,向量 x 的范数衡量从原点到点 x 的距离。
当 p = 2 时,L2范数被称为 欧几里得范数(Euclidean norm)。它表示从原点出发到向量 x 确定的点的欧几里得距离。L2范数在机器学习中出现地十分频繁,经常简化表示为||x||略去了下标 2。平方L2 范数也经常用来衡量向量的大小,可以简单地通过点积xTx 计算。
注意:平方 L2 范数在数学和计算上都比 L2 范数本身更方便。例如,平方 L2 范数对x 中每个元素的导数只取决于对应的元素,而 L2 范数对每个元素的导数却和整个向量相关。但是在很多情况下,平方 L2 范数也可能不受欢迎,因为它在原点附近增长得十分缓慢。在某些机器学习应用中,区分恰好是零的元素和非零但值很小的元素是很重要的。在这些情况下,我们转而使用在各个位置斜率相同,同时保持简单的数学形式的函数:L1 范数。L1 范数可以简化如下:
当机器学习问题中零和非零元素之间的差异非常重要时,通常会使用 L1 范数。每当x 中某个元素从 0 增加 ε,对应的 L 1 范数也会增加 ε。
另外一个经常在机器学习中出现的范数是 L ∞ 范数,也被称为 最大范数(max norm)。这个范数表示向量中具有最大幅值的元素的绝对值:
有时候我们可能也希望衡量矩阵的大小。在深度学习中,最常见的做法是使用 Frobenius 范数(Frobenius norm),F-范数。
2.6 特殊类型的矩阵和向量
2.7 特征分解
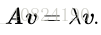
每个实对称矩阵都可以分解成实特征向量和实特征值:
2.8 奇异值分解
奇异值分解(singular value decomposition, SVD),将矩阵分解为奇异向量(singular vector)和 奇异值(singular value)。通过奇异值分解,我们会得到一些与特征分解相同类型的信息。然而,奇异值分解有更广泛的应用。每个实数矩阵都有一个奇异值分解,但不一定都有特征分解。例如,非方阵的矩阵没有特征分解,这时我们只能使用奇异值分解。
假设 A 是一个 m × n 的矩阵,那么 U 是一个 m × m 的矩阵,D 是一个 m × n的矩阵,V 是一个 n × n 矩阵。这些矩阵中的每一个经定义后都拥有特殊的结构。矩阵 U 和 V 都定义为正交矩阵,而矩阵 D 定义为对角矩阵。注意,矩阵 D 不一定是方阵。
对角矩阵 D 对角线上的元素被称为矩阵 A 的奇异值(singular value)。矩阵U 的列向量被称为左奇异向量(left singular vector),矩阵 V 的列向量被称 右奇异向量(right singular vector)。
事实上,我们可以用与 A 相关的特征分解去解释 A 的奇异值分解。A 的 左奇异向量(left singular vector)是 AAT 的特征向量。 A 的 右奇异向量(right singularvector)是ATA的特征向量。A 的非零奇异值是ATA特征值的平方根,同时也是AAT 特征值的平方根。
2.9 Moore-Penrose 伪逆
对于非方矩阵而言,其逆矩阵没有定义。Moore-Penrose 伪逆(Moore-Penrose pseudoinverse)使我们在这类问题上取得了一定的进展。矩阵 A 的伪逆定义为:
计算伪逆的实际算法没有基于这个定义,而是使用下面的公式:
2.10 迹运算
用迹运算表示表达式,我们可以使用很多有用的等式巧妙地处理表达式。例如,迹运算在转置运算下是不变的:
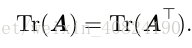
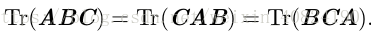
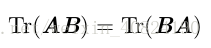
另一个有用的事实是标量在迹运算后仍然是它自己:a = Tr(a)。