1.功、平均值、概率
Ex:平均值:
ny1+y2+...+yn→b−a1∫zbf(x)dx

a=x0<x1<x2<...<xn=by1=f(x1),y2=f(x2),y3=f(x3)黎曼和:b−a(y1+....+yn)Δx→b−a∫abf(x)dx(Δx→∞)b−aΔx=n1
Ex:
f(x)=C求平均值。
b−a1∫abCdx=C
Ex:点在单位半圆上的平均高度

1−(−1)1∗∫−111−x2
dx=21∗2n=4π
Ex:上图弧长的平均值
(0≤θ≤π)
π1∫0θsinθdθ=−π1∗cosθ∣0π=π−1(−2)=π2
加权平均值:
∫abw(x)dx∫abf(x)w(x)dx
- 解释1:
AVC(C)=C
∫abw(x)dx∫abCw(x)dx=∫abw(x)dxC∫abw(x)dx=C
- 解释2:股票例子
w1+w2+w310w1+20w2+30w3
Ex:坩埚例子:

初始:
T=0
最终:
T=100−30y
能量= 体积 * 温度
∫01Tπx2dy=∫01(100−30y)πydy=∫01100πy−30πy2dy=50πy2−10πy3∣01=40π
最后的平均温度:
∫01πydy∫01Tπydy=2π40π=800
平常的平均温度:
2Tmax+Tmin=2100+70=850
2. 概率
Ex:
0<y<1−x2,使得
y>21的概率
∫−11(1−x2)dx∫211(1−x2)dx=P(x>21)
求概率的通常的公式:
a≤x1≤x2≤b,P(x1<x<x2)=∫abw(x)dx∫x1x2w(x)dx=TotalPart
Ex:靶子问题:
f=Ce−r2(模型)


PART=∫r1r22πre−r2dr=−πe−r2∣r1r2=π(e−r12−e−r22)PART=Cπ(e−r12−e−r22)Whole=Cπ(e02−e−∞2)=CπWHOLEPART=er12−er22
Ex:假设在靶子旁边站着一个人。求小人被射中的概率。
122∗P(2a<r<3a)=?
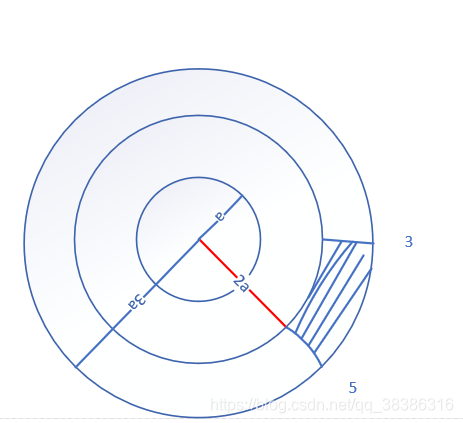
P(0<r<a)=21e−02−e−a2=21e−a2=21P(2a<r<3a)=e−(2a)2−e−(3a)2=e(−a2)4−e(−a2)9=(21)4−219≈161
122∗P(2a<r<3a)=321.
权重为:
w(r)=2πcte−2





