多变量微积分笔记22——空间曲面的通量

　　在上一章中，我们知道了怎样计算球面和柱面的通量，但是很多时候，空间的曲面不容易用球坐标或柱坐标表示，此时怎样计算通量？

曲面S的通量

　　上一章提到，在空间向量场F中有一个曲面S，S的通量是：

 

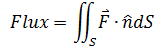
　　我们使用不同的方法在各种情况下得到面积积元dS和单位法向量n，比如在球面和柱面中使用球坐标和柱坐标。但是对于其它曲面应当如何处理？如下图所示，假设S是 z = f(x,y)的图像，如何计算在向量场中S的通量？

 

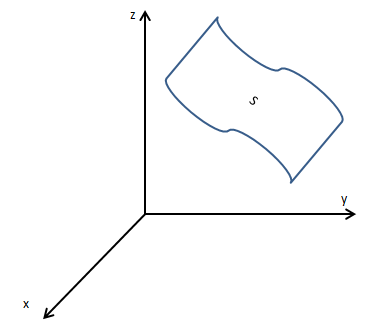
　　现在将S投影到xy平面，如下图所示：

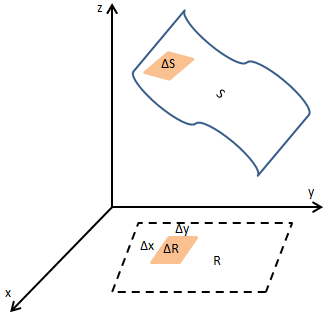
　　ΔS和ΔR是S和R上的小矩形，其中ΔR是ΔS的投影，Δx和Δy分别是ΔR的两边。当然，由于S可能是弯曲的，ΔS也会稍有弯折，但当其足够小时，大体上是个矩形。为了不至于太过混乱，下图将ΔS和ΔR放大并单独展示：

　　ΔR的一个顶点的值是(x,y,0)，它在ΔS上对应的点是(x,y,z)。将ΔS的两个临边用向量u和v表示，它们的叉积就是ΔS的面积：

 

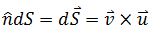
　　上式将单位向量化简为dS，而叉积除了表示面积大小外，也表示了方向信息。现在，问题转换为计算u × v。

　　已知v的起点是(x,y,z)，终点是(x, y+Δy, z+Δz)，其中：

　　同理：

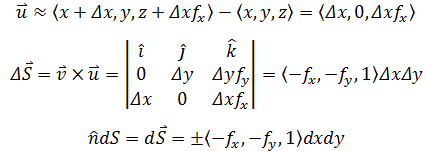
　　最终得到通量计算公式：

 

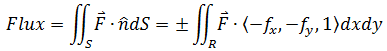
　　正负号取决于法向量的方向。因为等式右侧已经变成了xy平面的二重积分，所以出于习惯，积分域由S变成了R。

曲面的积分域

　　如下图所示，求F = zk通过z = x² + y²在单位圆上方曲面的通量。

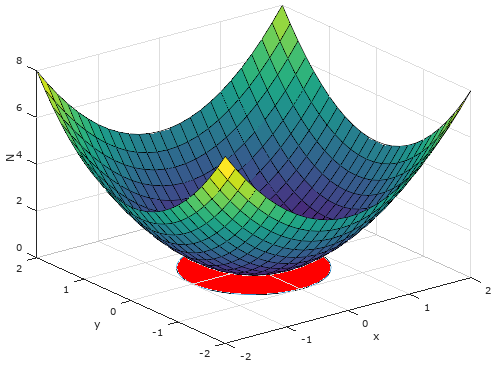
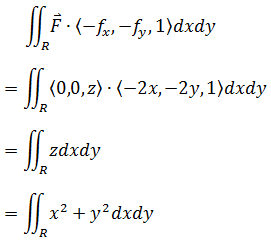
　　现在问题转换为如何求得曲面的积分域，从而使上式变成普通的二重积分。这需要借助曲面在xy平面的投影，在本例中，曲面的投影恰好是单位圆，可以使用极坐标处理：

 

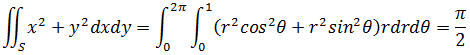
示例

　　函数z = x² + y的一块区域中在xy平面的投影是单位正方形，并起这块区域满足z > 0，计算该区域在场F = zi + xk中的通量。

　　如果是求向上的通量，根据公式：

 

 

---

 

作者：我是8位的

出处：http://www.cnblogs.com/bigmonkey

本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

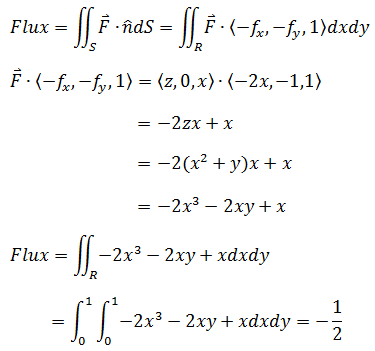
扫描二维码关注公众号“我是8位的”