1.定积分在对数和几何上的应用
FTC2:
dxd∫axf(t)d(t)=f(x)y′=x1;L(x)=∫1xtdtL′(x)=x1;L(x)=∫11tdt=0L′′=−x21L(1)=0;L′(1)=1
L(e)=1,
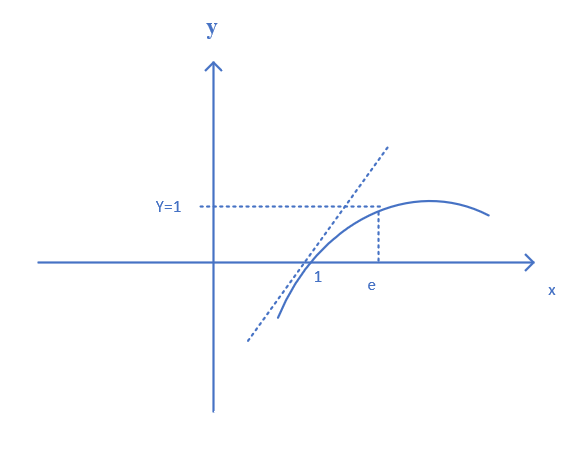
为什么
L(x)<0,x<1???
- L(1) = 0 , L递增
-
L(x)=∫1xtdt=−∫x1tdt
L(ab)=L(a)+L(b)∫1abtdt=∫1atdt+∫aabtdt由于∫aabtdt=∫1bauadu=∫1budu=L(b)t=au,dt=adu
Ex:
∫0xe−t2dt
F′(x)=e−x2,F(0)=0,F′(0)=e02=1F′′=−2xe−x2{<0>0,x>0,x<0
如图所示:
F′′图像,虚线为
y=2π
,为奇函数,
F(−x)=−F(x)
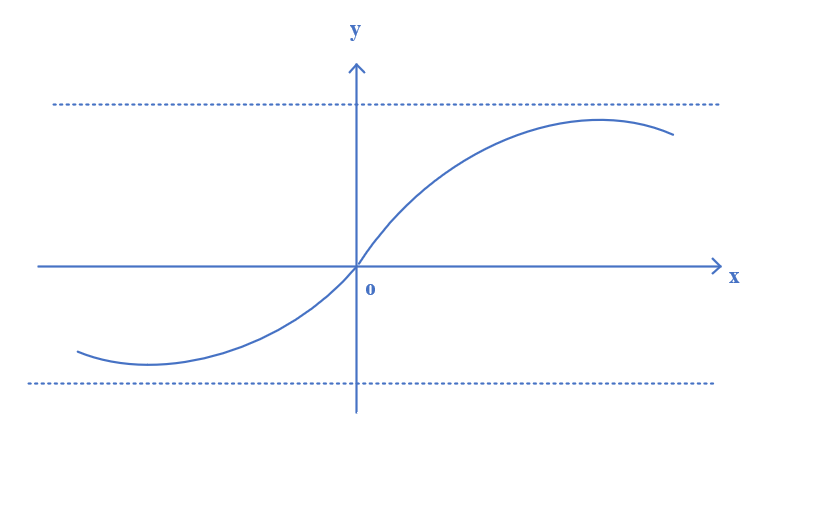
如图所示:
F′=e−x2
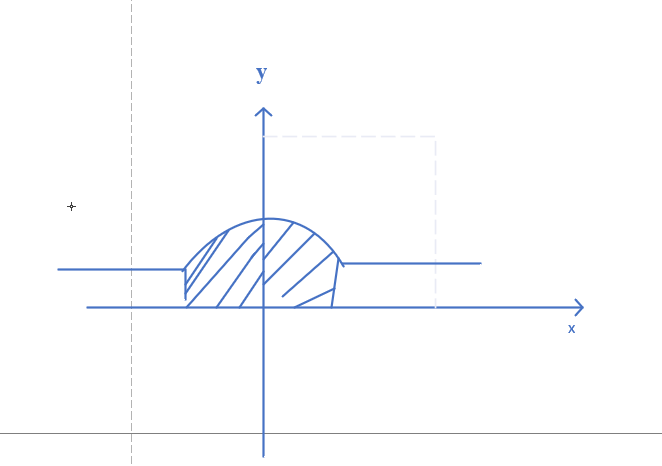
limx→∞F(x)=2π
erf(x)=π
2∫0xe−t2dt=z2
扩展的特殊函数:
-
Li(x)=∫2xlntdt≈primes(素数个数)<x
-
C(x)=∫0xcos(t2)dtS(x)=∫0xsin(t2)dt}菲涅耳积分H(x)=∫0xtsintdt(傅里叶级数)
Ex:关于曲线积分围城的面积
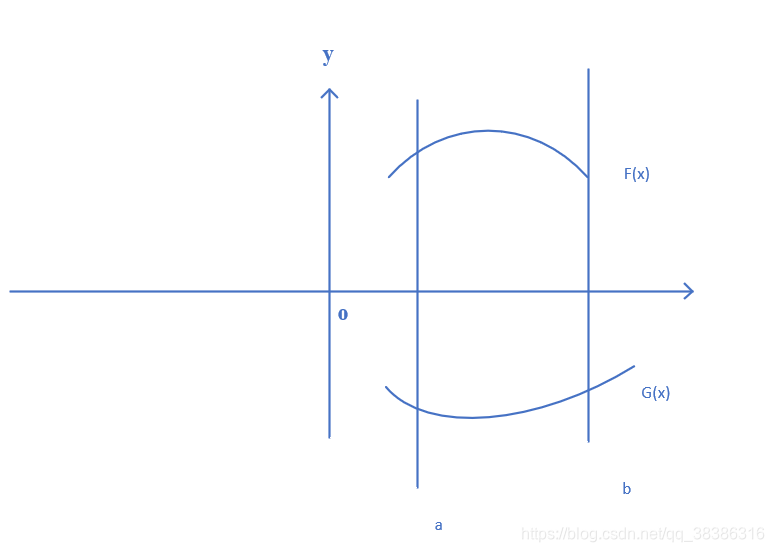
Area=∫ab(f(x)−g(x))dx
Ex求
x=y2和
y=x−2围成的面积。
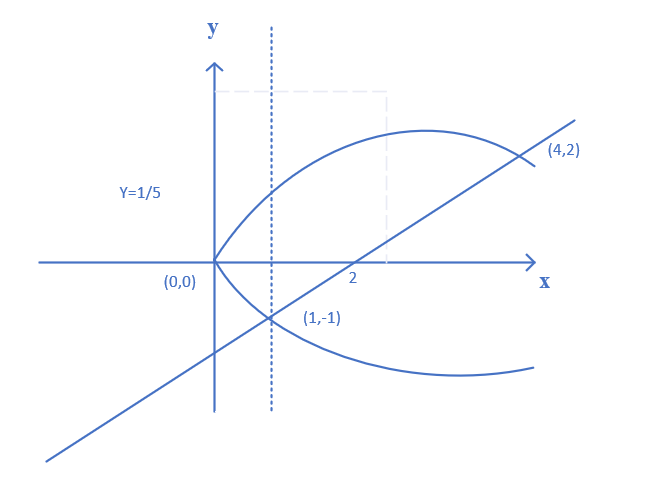
- (垂直切分)
Area=∫01(x
−(−x
))dx+∫14(x
−(x−2))dx=...
- (横向切分)
Area=∫−12((y+2)−y2)dy=(2y2+2y−3y3)∣−12=29




