1.1 线性代数

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/egbert123/article/details/86221840

import tensorflow as tf
import numpy as np

标量，就是一个单独的数

向量，一列数

矩阵，一个二维数组

张量，tensorflow 中，所有变量用张量tensor表示

转置，行列互变

a = 10  #标量
b = tf.constant(a)   # 0阶张量
print(a)
print(b)

A = [1, 2, 3] # 向量
B = tf.constant(A) # 1阶张量
print(A)
print(B)

A_ = [[1,2,3], [4,5,6]]  # 矩阵
B_ = tf.constant(A_, dtype=tf.float32)   # 2阶张量
print(A_)
print(B_)

B_T = tf.transpose(B_) # 转置后的张量
print(B_T)

C_ = [[1,2,3], [4,5,6]]  # 矩阵
D_ = tf.constant(C_)   # 2阶张量
F = C_ + D_
print(F)

10
Tensor("Const_45:0", shape=(), dtype=int32)
[1, 2, 3]
Tensor("Const_46:0", shape=(3,), dtype=int32)
[[1, 2, 3], [4, 5, 6]]
Tensor("Const_47:0", shape=(2, 3), dtype=float32)
Tensor("transpose_5:0", shape=(3, 2), dtype=float32)
Tensor("add_3:0", shape=(2, 3), dtype=int32)

张量

是tensorflow中的数据管理形式，在tensorflow中所有的数据都通过张量的形式来表示（从上面的例子可以看出来），张量并没有正真的保存数字，它保存的是如何得到这些数字的计算过程，张量中主要保存三个属性：名字，维度，类型。

如果想要得到计算结果，需要将张量放在session中运行。

with tf.Session() as sess:
    f = sess.run(F)
    print(f)
    sess.close()

[[ 2  4  6]
 [ 8 10 12]]

矩阵和向量的相乘

最重要的是A(m, n), B(n, k) --> C(m, k) 维度符合才能乘。

M = tf.matmul(B_, B_T)
print(M)

Tensor("MatMul_4:0", shape=(2, 2), dtype=float32)

单位矩阵和逆矩阵

I1 = tf.eye(3)
I2 = tf.eye(2, 3)
print(I1)
print(I2)
M_inv = tf.matrix_inverse(M)  # 逆矩阵，只接收float类型
print(M_inv)

Tensor("eye_10/MatrixDiag:0", shape=(3, 3), dtype=float32)
Tensor("eye_11/MatrixSetDiag:0", shape=(2, 3), dtype=float32)
Tensor("MatrixInverse_2:0", shape=(2, 2), dtype=float32)

线性相关和生成子空间

如果一组向量中的任意一个向量都不能表示成其它向量的线性组合，那么这组向量称为线性无关。

如果某个向量是一组向量中某些向量的线性组合，那么我们将这个向量加入到这组向量后不会增加这组向量的生成子空间。

范数（衡量一个向量的大小）

$||x||_p = (\Sigma|x_i|^p )^\frac {1} {p}$

直观上向量x的范数是衡量从原点到点x的距离。

当p = 2时， $L^2$范数被称为欧几里得范数，表述从原点出发到向量x确定点的欧几里得距离(其实就是所有的值的平方的和的平方根), $L^2$范数在机器学习中用的比较多，主要用在正则化等技术中，后面会有涉及，它可以简单的通过点积 $x^Tx$计算

与 $L^2$类似，我们想衡量矩阵大小，在深度学习中常用Frobenius范数，有很多资料将 $L^2$和 $L^F$认为相同。

当p=1时， $L^1$范数，在机器学习应用中，区分恰好是0的元素和非零但值很小的元素， $||x||_1 = (\sum|x_i| )$

当p=0时， $L^0$范数，用来统计向量中非零元素的个数，通过非零元素个数衡量向量大小。

当 $p=\propto$
时， $L^\propto$范数，也称为最大范数。表示向量中最大幅值的原色的绝对值。

关于范数，有篇文章写的比较好，引用一下 https://blog.csdn.net/yangpan011/article/details/79461846

# 我们可以用ord=’euclidean’的参数来调用tf.norm来求欧基里得范数
a02 = tf.constant([1,2,3,4],dtype=tf.float32)  # 向量
a03 = tf.constant([[1,2],[3,4]],dtype=tf.float32)  # 矩阵
with tf.Session() as sess:   
    L2 = sess.run(tf.norm(a02, ord='euclidean')) # L2范数
    L_F = sess.run(tf.norm(a03, ord=2))  # 矩阵的范数称为Frobenius范数
    L1 = sess.run(tf.norm(a03,ord=1))   # L1范数
    L_MAX = sess.run(tf.norm(a03,ord=np.inf))  # L∝范数
    print(L2)
    print(L_F)
    print(L1)
    print(L_MAX)
    sess.close()

5.477226
5.477226
10.0
4.0

特殊类型的矩阵和向量

对角矩阵

对称矩阵 $A=A^T$

单位向量 $||x|| = 1.$

正交 $x^Ty = 0$

正交矩阵 $A^TA = AA^T = I$

特征分解：

将矩阵分解成一组特征向量和特征值

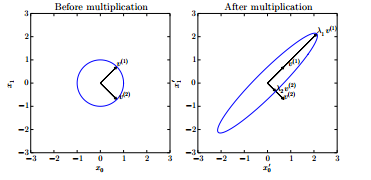
矩阵A有两个标准的正交的特征向量，对应的特征值为 $\lambda_1$的 $v^{(1)}$以及特征值为 $\lambda_2$的 $v^{(2)}$， 从图中可以看出，A将单位圆 $v^{(i)}$拉伸了 $\lambda_i$倍

所有特征值都是正数的矩阵称为正定

所有特征值都是非负数的矩阵称为半正定

所有特征值都是负数的矩阵称为负定

所有特征值都是非正数的矩阵称为半负定

A = tf.truncated_normal([3, 3])  # 截断正太分布，当mean=0, stddev=1时，生成的数在[-2,2]（方差的两倍内）
with tf.Session() as sess:
    print(sess.run(A))
    eigenvalues, eignvectors = sess.run(tf.self_adjoint_eig(A))
    print(eigenvalues)
    print(eignvectors)
    sess.close()

[[-1.2078785  -1.6885282   0.6439421 ]
 [ 0.671624    1.9556671   0.90718263]
 [-1.7275476   0.06104081  1.0154626 ]]
[-0.8078741  0.8497921  1.9737738]
[[-0.06946777 -0.98544115 -0.15517797]
 [-0.4434218   0.16984437 -0.88007396]
 [-0.8936171  -0.00767255  0.44876486]]

奇异值分解（SVD）

将矩阵分解为奇异向量（singular value）和奇异值（singular vector）

与特征分解类似，只不过奇异值分解需要将矩阵A分解成三个矩阵的乘积：
$A = UDV^T$

其中A(m,n), U(m,m), D(m,n), V(n, n)

对角矩阵D对角线上的元素称为矩阵A的奇异值，矩阵U的列向量被称为左奇异向量，矩阵U的列向量被称为右奇异向量。

As =tf.constant( [[1,2,3],[4,5,6]], dtype=tf.float64)
As_svd = tf.svd(As, full_matrices=True)
# full_matrices：如果为 true，则计算全尺寸的 u 和 v
with tf.Session() as sess:
    print(sess.run(As))
    s,u,v = sess.run(As_svd)
    print(s)
    print(u)
    print(v)
    sess.close()
   
    # s：奇值
    # u：奇左向量
    # v ：奇右向量

[[1. 2. 3.]
 [4. 5. 6.]]
[9.508032   0.77286964]
[[-0.3863177  -0.92236578]
 [-0.92236578  0.3863177 ]]
[[-0.42866713  0.80596391  0.40824829]
 [-0.56630692  0.11238241 -0.81649658]
 [-0.7039467  -0.58119908  0.40824829]]

Moore-Penrose伪逆

若有A与其左逆B，有 $Ax=y$ 以及 $x=By$, 则则Moore-Penrose伪逆为 $A^+=VD^+U^T$
U,D,V是矩阵A奇异值分解后得到的矩阵，对角矩阵的伪逆 $D^+$是其非零元素取倒数之后再转置得到的。
A 的列数大于行数，得到就是所有可行解中 $L_2$范数最小的一个，如果相反，就是 $||Ax−y||$最小。

迹运算

迹运算返回的是矩阵的对角元素的和

Fobenius 范数 $||A||_F = \sqrt{Tr{(AA^T)}}$

x = tf.constant([[1, 2], [3, 4]])
tr = tf.trace(x)  # 5
with tf.Session() as sess:
    print(sess.run(tr))
    sess.close()

5

行列式

det(A)，将方阵A映射到实数的函数

主成分分析（PCA） 降维，压缩

应用：

假设对100100的图片进行分析，那么100100=10000个特征

第一步是将10000个特征利用PCA压缩为1000个特征

第二部是对训练集运行学习算法（压缩后的特征集）

注意:

PCA只是在训练集上使用，在交叉和测试集上不适用

训练最好还是使用原始的特征，除非算法运行太慢，或者占用太多内存情况下

原理:

假设有m个点{ $x^{(1)},...,x^{(m)}$}，如果想对这些点进行有损压缩，减小内存使用，同时希望损失的精度最小。

encode : f(x) = c

decode : x ≈ g(f(x)) 来近似x

我们选g© = Dc, 其中D是定义解码器的矩阵

为了又唯一解，限制D中所有列向量都有单位范数

1 、找到encode : 假设最优编码为 $c^*$

$c^* = argmin{||x - g(c)||}_2^2$

展开优化后最有得到 $c = D^Tx$, 那么 $x≈r(x) = g(c) = Dc = DD^Tx$

2、找到decode :

利用Frobenius范数，对所有维度和所有点进行解码，所以要最小化所有维度所有点的误差矩阵范数（最小化距离）

$D^* = argmin\sqrt{\sum(x - r(x))^2} = I_l$
带入 $d^* = argmin{\sum||x^{(i)} - dd^Tx^{(i)}||}_2^2 = 1$

所以变成最小化问题 $argmin||X-Xdd^T||^2_2 = argminTr((X-Xdd^T)^T(X-Xdd^T))$ (迹运算)

将上面展开，去掉无关项，得到：
$argmaxTr(d^TX^TXd)$ subject to $d^Td = 1$
通过特征分解得到最优的d是 $X^TX最大的特征值对应的特征向量$

所以得到decode

类似的降维技术还有t-SNE 和自编码器