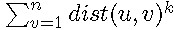
复杂度大概O(nk)
一些尝试:
1.对每个点推出1,2,3,,,到k次方的值。但是临项递推二项式展开也要考虑到具体每个点的dist
2.相邻k次方递推呢?递推还是不能避免k次方的展开
k次方比较讨厌,于是考虑用斯特林数处理
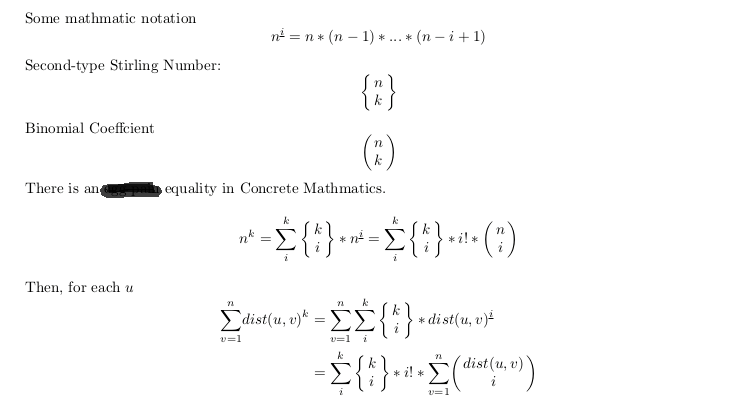
转化成求k个后面这个C(dis,i)
组合数相比较于k次方有什么好处呢?
有直接的简单的递推式!
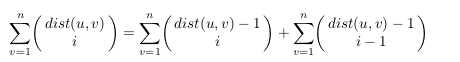
并且恰好的是,可以直接树形dp,距离对于子树恰好-1
O(nk)树形dp一遍
然后换根O(nk)再处理一遍
回到主函数,把之前的那些东西在分别乘上加起来即可。
#include<bits/stdc++.h> #define reg register int #define il inline #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=50000+5; const int K=505; const int mod=10007; int n,k,t; struct node{ int nxt,to; }e[2*N]; int hd[N],cnt; int f[N][K]; int g[N][K]; int jie[K],s[K][K]; void add(int x,int y){ e[++cnt].nxt=hd[x]; e[cnt].to=y; hd[x]=cnt; } void dfs(int x,int fa){ for(reg i=hd[x];i;i=e[i].nxt){ int y=e[i].to; if(y==fa) continue; dfs(y,x); for(reg j=0;j<=k;++j){ if(j)f[x][j]=(f[x][j]+f[y][j]+f[y][j-1])%mod; else f[x][j]=(f[x][j]+f[y][j])%mod; } } f[x][0]=(f[x][0]+1)%mod; } void sol(int x,int fa){ if(x==1){ for(reg j=0;j<=k;++j) g[x][j]=f[x][j]; } else{ for(reg j=0;j<=k;++j){ if(j>1) g[x][j]=(f[x][j]+(g[fa][j]-(f[x][j]+f[x][j-1])+mod)%mod+(g[fa][j-1]-(f[x][j-1]+f[x][j-2]))%mod+mod+mod)%mod; else if(j==1) g[x][j]=(f[x][j]+(g[fa][j]-(f[x][j]+f[x][j-1])+mod)%mod+(g[fa][j-1]-(f[x][j-1]))%mod+mod+mod)%mod; else g[x][j]=n; } } for(reg i=hd[x];i;i=e[i].nxt){ int y=e[i].to; if(y==fa) continue; sol(y,x); } } void clear(){ cnt=0; memset(hd,0,sizeof hd); memset(f,0,sizeof f); memset(g,0,sizeof g); } int main(){ rd(t); s[0][0]=1; for(reg i=1;i<=501;++i){ for(reg j=1;j<=501;++j){ s[i][j]=(s[i-1][j-1]+j*(s[i-1][j])%mod)%mod; } } jie[0]=1; for(reg i=1;i<=501;++i) jie[i]=jie[i-1]*i%mod; while(t--){ clear(); rd(n);rd(k); int x,y; for(reg i=1;i<n;++i){ rd(x);rd(y); add(x,y);add(y,x); } dfs(1,0); // for(reg i=1;i<=n;++i){ // cout<<" ii "<<i<<endl; // for(reg j=0;j<=k;++j){ // cout<<" f[i]["<<j<<"]"<<" : "<<f[i][j]<<endl; // }cout<<endl; // }cout<<endl; sol(1,0); // for(reg i=1;i<=n;++i){ // cout<<" ii "<<i<<endl; // for(reg j=0;j<=k;++j){ // cout<<" g[i]["<<j<<"]"<<" : "<<g[i][j]<<endl; // }cout<<endl; // }cout<<endl; for(reg i=1;i<=n;++i){ int ans=0; for(reg j=1;j<=k;++j){ ans=(ans+jie[j]*s[k][j]%mod*g[i][j]%mod)%mod; } printf("%d\n",ans); } } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/12/29 19:09:56 */
总结:
这个就真的比较有趣了
把n^k换成斯特林数,还有一个原因是n^k实在不好支持递推
组合数就比较轻松了。
恰好树形dp的递推特点和组合数的递推式又比较好的吻合在一起!
(当然,n的i次下降幂也有不错的递推性质,也可以不用转化成组合数直接类比递推,本质相同。)