\(\hspace{2em}\)关于判断函数的单调性问题,教材上所举例子是从数的角度求解导函数的正负,从而判断原函数的单调性,所以学生就依葫芦画瓢,碰到这类问题都这样做,但是他会发现在高三中的大多这类题目都不能,这当碰到不能从数的角度求解的题目时思路自然会受阻而放弃,其实只需要老师做引导,如果从数的角度不能突破,可以考虑从形的角度入手分析,这类题目反倒会顺利求解。
一、用导函数的图像判断原函数的单调性
【例1】已知函数\(f(x)=2x^3+ax^2+bx+1\)的导函数为\(f'(x)\),若函数\(y=f'(x)\)的对称轴是\(x=-\cfrac{1}{2}\),且\(f'(1)=0\)
(1).求\(a,b\)的值。
(2).判断函数的单调性,并求函数的极值。
【分析】(1)通过导函数方程和二次函数对称轴方程建立方程组,即可解得a、b,
(2)数字系数的三次多项式函数求极值,用常规的思路和步骤求解即可。
【解答】(1)由于\(f'(x)=6x^2+2ax+b\),且对称轴为\(x=-\cfrac{1}{2}\),
则有\(-\cfrac{a}{6}=-\cfrac{1}{2}\),则\(a=3\),
又由于\(f'(1)=0\),则\(6+2a+b=0\),解得\(b=-12\),
所以\(a=3,b=-12\)。
(2)因为\(f(x)=2x^3+3x^2-12x+1\),\(f'(x)=6x^2+6x-12=6(x^2+x-2)\)
辅助图像
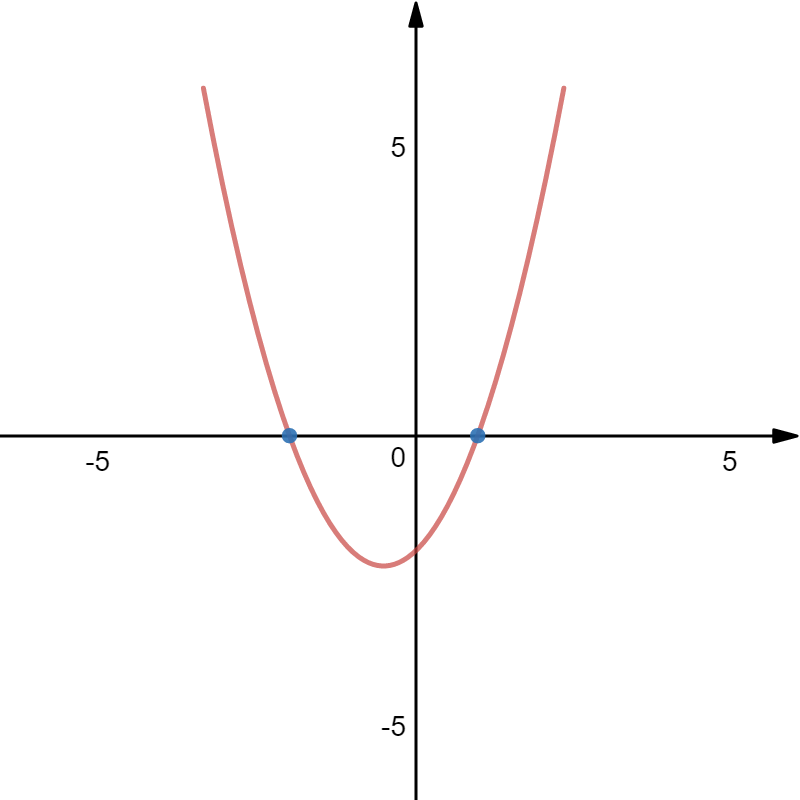
常规的解法这样写道:
令\(f'(x)≥0\),即\(x^2+x-2≥0\),解得\(x≥1\)或\(x≤-2\),
令\(f'(x) ≤0\),即\(x^2+x-2 ≤0\),解得$ -2≤x ≤1$,
有了辅助图像后,我们这些写:
当\(x< -2\)时,\(f'(x)>0\),\(f(x)\)单调递增;
当\(-2<x<1\)时,\(f'(x)<0\),\(f(x)\)单调递减;
当\(x>1\)时,\(f'(x)>0\),\(f(x)\)单调递增;
然后做总结:
所以函数\(f(x)\)在\((-2,1)\)上单调递减,在\((-\infty,-2)\)和\((1,+\infty)\)上单调递增,
当\(x=-2\)时,\(f(x)\)取得极大值,为\(f(-2)=21\),
当\(x=1\)时,\(f(x)\)取得极小值,为\(f(1)=-6\)。
二、用导函数的分子图像判断原函数的单调性
已知函数\(f(x)=x^2+2mlnx-(m+4)x+lnm+2\).(Ⅱ)当\(m>0\)时,试讨论函数\(f(x)\)的单调性;
【分析】(Ⅱ)借助导函数的分子函数的动态图像,即可判断导函数的正负,从而判断原函数的单调性。
【解答】辅助图像
(Ⅱ)\(f'(x)=2x+\cfrac{2m}{x}-(m+4)=\cfrac{2x^2-(m+4)x+2m}{x}=\cfrac{(x-2)(2x-m)}{x}\),
令\(f'(x)=0\),得到\(x=2\)或\(x=\cfrac{m}{2}>0\),只需要借助分子函数的图像,即可判断导函数的正负,
当\(0<\cfrac{m}{2}<2\)时,即\(0<m<4\)时, \(x\in (0,\cfrac{m}{2})\)时,\(f'(x)>0\),\(f(x)\)单调递增,
\(x\in (\cfrac{m}{2},2)\)时,\(f'(x)<0\),\(f(x)\)单调递减,\(x\in (2,+\infty)\)时,\(f'(x)>0\),\(f(x)\)单调递增,
当\(\cfrac{m}{2}=2\)时,即\(m=4\)时,此时\(f'(x)\ge 0\)恒成立,
当且仅当\(x=2\)时取得等号,故\(f(x)\)在\((0,+\infty)\)上单调递增,
当\(\cfrac{m}{2}>2\)时,即\(m>4\)时, \(x\in (0,2)\)时,\(f'(x)>0\),\(f(x)\)单调递增,
\(x\in (2,\cfrac{m}{2})\)时,\(f'(x)<0\),\(f(x)\)单调递减, \(x\in (\cfrac{m}{2},+\infty)\)时,\(f'(x)>0\),\(f(x)\)单调递增,
综上所述,
当\(0<m<4\)时, \(x\in (0,\cfrac{m}{2})\)时,\(f(x)\)单调递增,
\(x\in (\cfrac{m}{2},2)\)时,\(f(x)\)单调递减,
\(x\in (2,+\infty)\)时,\(f(x)\)单调递增,
当\(m=4\)时,\(f(x)\)在\((0,+\infty)\)上单调递增,
当\(m>4\)时, \(x\in (0,2)\)时,\(f(x)\)单调递增,
\(x\in (2,\cfrac{m}{2})\)时,\(f(x)\)单调递减,
\(x\in (\cfrac{m}{2},+\infty)\)时,\(f(x)\)单调递增,
三、用导函数中的一部分函数图像判断原函数的单调性
已知函数\(f(x)=x^2+(m+2)x+1(m为常数)\).(Ⅰ)讨论函数\(g(x)=e^xf(x)\)的单调性;
【分析】(Ⅰ)求导后借助导函数的部分函数\(y=(x+1)(x+m+3)\)的图像,
利用两根的大小关系分类讨论,可以轻松判断其单调性;
【解答】(Ⅰ)\(g(x)=e^x[x^2+(m+2)x+1]\),定义域为\(R\),
则\(g'(x)=e^x\cdot [x^2+(m+2)x+1]+e^x\cdot (2x+m+2)\)
\(=e^x[x^2+(m+4)x+m+3]=e^x(x+1)[x+(m+3)]\)
令\(g'(x)=0\),得到\(x=-1\)或\(x=-(m+3)\),由于\(e^x>0\)恒成立,
故借助开口向上的二次函数\(y=(x+1)[x+(m+3)]\)的图像求解如下:
①当\(-(m+3)<-1\)时,即\(m>-2\)时,
\(x\in (-\infty,-m-3)\)时,\(g'(x)>0\),\(g(x)\)单调递增,
\(x\in (-m-3,-1)\)时,\(g'(x)<0\),\(g(x)\)单调递减,
\(x\in (-1,+\infty)\)时,\(g'(x)>0\),\(g(x)\)单调递增,
②当\(-(m+3)=-1\)时,即\(m=-2\)时,\(g'(x)\ge 0\)恒成立,
当且仅当\(x=-1\)时取得等号,故\(g(x)\)在R上单调递增;
③当\(-(m+3)>-1\)时,即\(m<-2\)时,
\(x\in (-\infty,-1)\)时,\(g'(x)>0\),\(g(x)\)单调递增,
\(x\in (-1,-m-3)\)时,\(g'(x)<0\),\(g(x)\)单调递减,
\(x\in (-m-3,+\infty)\)时,\(g'(x)>0\),\(g(x)\)单调递增,
综上所述:
当\(m<-2\)时,函数\(g(x)\)的单增区间为\((-\infty,-1)\)和\((-m-3,+\infty)\),单减区间为$ (-1,-m-3)$;
当\(m=-2\)时,函数\(g(x)\)只有单增区间为\((-\infty,+\infty)\);
当\(m>-2\)时,函数\(g(x)\)的单增区间为\((-\infty,-m-3)\)和\((-1,+\infty)\),单减区间为$ (-m-3,-1)$;
四、用导函数的几个因子函数的图像和符号法则判断导函数的正负
已知函数\(f(x)=(x-2)e^x+a(x-1)^2\).讨论\(f(x)\)的单调性.
【分析】利用导函数分解因式后的两个因式函数的图像和符号法则判断导函数的正负,
从而判断原函数的单调性。
【解答】定义域为\(R\),\(f'(x)=1\cdot e^x+(x-2)\cdot e^x+2a(x-1)=e^x(x-1)+2a(x-1)=(x-1)(e^x+2a)\),
在同一个坐标系中做出函数\(y=x-1\)(定图)和函数\(y=e^x+2a\)(动图)的图像,
根据动图\(y=e^x+2a\)是否与\(x\)轴有交点分类讨论如下:
①当\(2a\ge 0\)时,即\(a\ge 0\)时,恒有\(e^x+2a>0\),
当\(x\in (-\infty,1)\)上时,\(x-1<0\) ,则\(f'(x)=(e^x+2a)(x-1)<0\),故\(f(x)\)单调递减,
当\(x\in (1,+\infty)\)上时,\(x-1>0\) ,则\(f'(x)=(e^x+2a)(x-1)>0\),故\(f(x)\)单调递增,
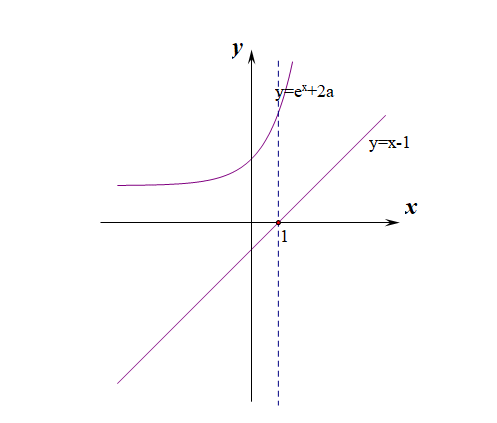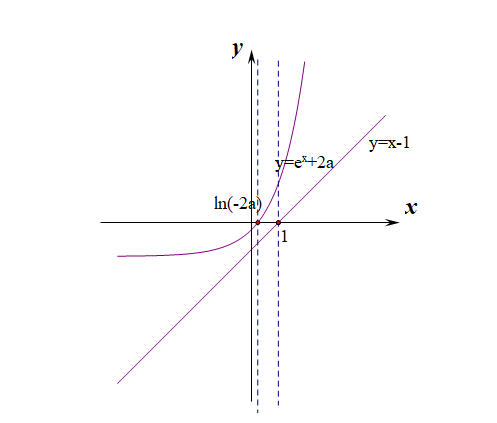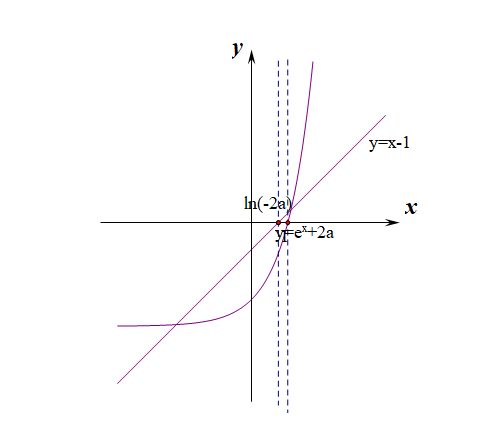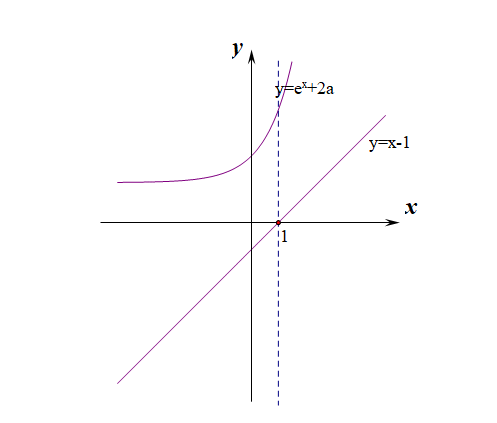
当\(2a<0\)时,即\(a<0\)时,\(y=e^x+2a\)与\(x\)轴有交点,令\(e^x+2a=0\),解得\(x=ln(-2a)\),
然后针对\(ln(-2a)\)与\(1\)的大小关系继续细分如下
②当\(ln(-2a)<1\)时,即\(-\cfrac{e}{2}<a<0\)时,
当\(x\in(-\infty,ln(-2a))\)时,\(e^x+2a<0\),\(x-1<0\),则\(f'(x)>0\),\(f(x)\)单调递增;
当\(x\in(ln(-2a),1)\)时,\(e^x+2a>0\),\(x-1<0\),则\(f'(x)<0\),\(f(x)\)单调递减;
当\(x\in(1,+\infty)\)时,\(e^x+2a>0\),\(x-1>0\),则\(f'(x)>0\),\(f(x)\)单调递增;
③当\(ln(-2a)=1\)时,即\(a=-\cfrac{e}{2}\)时,
当\(x\in(-\infty,1)\)时,\(e^x+2a<0\),\(x-1<0\),则\(f'(x)>0\),\(f(x)\)单调递增;
当\(x\in(1,+\infty)\)时,\(e^x+2a>0\),\(x-1>0\),则\(f'(x)>0\),\(f(x)\)单调递增;
即\(x\in (-\infty,+\infty)\)时,恒有\(f'(x)\ge 0\),当且仅当\(x=1\)时取到等号,故\(f(x)\)单调递增;
④当\(ln(-2a)>1\)时,即\(a<-\cfrac{e}{2}\)时,
当\(x\in(-\infty,1)\)时,\(e^x+2a<0\),\(x-1<0\),则\(f'(x)>0\),\(f(x)\)单调递增;
当\(x\in(1,ln(-2a))\)时,\(e^x+2a<0\),\(x-1>0\),则\(f'(x)<0\),\(f(x)\)单调递减;
当\(x\in(ln(-2a),+\infty)\)时,\(e^x+2a>0\),\(x-1>0\),则\(f'(x)>0\),\(f(x)\)单调递增;
综上所述,
当\(a<-\cfrac{e}{2}\)时,单增区间为\((-\infty,1)\)和\((ln(-2a),+\infty)\),单减区间为\((1,ln(-2a))\);
当\(a=-\cfrac{e}{2}\)时,只有单增区间为\((-\infty,+\infty)\);
当\(-\cfrac{e}{2}<a<0\)时,单增区间为\((-\infty,ln(-2a))\)和\((1,+\infty)\),单减区间为\((ln(-2a),1)\);
当\(a\ge 0\)时,单减区间为\((-\infty,1)\),单增区间为\((1,+\infty)\);
【点评】由于教材上所举例子是从数的角度求解导函数的正负,从而判断原函数的单调性,
故许多学生碰到这个题目时思路会受阻,需要老师做引导,如果从数的角度不能突破,可以考虑从形的角度入手分析。
五、用二阶导判断一阶导的正负
设函数\(f(x)=\cfrac{1}{2}{x^2}+aln(1+x)\).(Ⅱ)若\(a=1\),证明:当\(x>0\)时,\(f(x)<e^x-1\).
【分析】(Ⅱ)先转化为恒成立求最大值问题,先求一阶导,此时不好判断其正负,再求二阶导,
由二阶导的正负判断一阶导的增减性,进而知道一阶导的正负,从而知道原函数的单调性。
【解答】(Ⅱ)当\(a=1\)时,\(f(x)=\cfrac{1}{2}{x^2}+ln(x+1)\),欲证明\(x >0\) 时,\(f(x)<e^x-1\),
即证明x>0时,\(\cfrac{1}{2}{x^2}+ln(x+1)-e^x+1<0\)恒成立。
令\(g(x)=\cfrac{1}{2}{x^2}+ln(x+1)-e^x+1\),只需要证明\(g(x)_{max}<0\)即可。
\(g'(x)=x+\cfrac{1}{x+1}-e^x\),令\(h(x)=x+\cfrac{1}{x+1}-e^x\),
则\(h'(x)=1-e^x-\cfrac{1}{(1+x)^2}\),当\(x>0\)时,\(h'(x)<0\)恒成立,
故函数\(g'(x)\)单调递减,则有\(g'(x)<g'(0)=0\),即有\(x >0\)时,\(g'(x)<0\)恒成立,
则\(x>0\)时,函数\(g(x)\)单调递减,即有\(g(x)<g(0)=0\)恒成立,
即证明了\(x>0\)时,\(f(x)<e^x-1\)。
(Ⅱ)用导数证明不等式时,有一个很常用的思路是作差构造新函数,转而求新函数的最值或最值的极限大于小于0。
还有一个常用思路是连求两次导数,用二阶导的正负先判断一阶导的增减,再利用一阶导的增减在端点处的值再判断一阶导的正负,从而知道原函数的增减性。
六、含有\(e^x\)和\(lnx\)的导函数寻找分界点判断导函数的正负
已知函数\(f(x)=e^x-ax-1(a∈R)\),\(g(x)=lnx\).(I)若不等式\(f(x)≥g(x)\)对任意的\(x∈(0,+\infty)\)恒成立,求实数a的取值范围;
【解答】(I)由题目可知,\(e^x-ax-1\ge lnx\)对任意的\(x∈(0,+\infty)\)恒成立,
分离参数得到,\(a\leq \cfrac{e^x-1-lnx}{x}(x>0)\);
令\(h(x)= \cfrac{e^x-1-lnx}{x}\),需要求\(h(x)_{min}\),
\(h'(x)=\cfrac{(e^x-\frac{1}{x})\cdot x-(e^x-1-lnx)\cdot 1}{x^2}\)
\(=\cfrac{xe^x-1-e^x+1+lnx}{x^2}\)
\(=\cfrac{(x-1)e^x+lnx}{x^2}\)
观察分子的结构,可以发现两部分\((x-1)e^x\)和\(lnx\)的零点都是\(x=1\),故有
当\(x\in(0,1)\)时,\(x-1<0\),\(lnx<0\),则\(h'(x)<0\),\(h(x)\)单调递减;
当\(x\in(1,+\infty)\)时,\(x-1>0\),\(lnx>0\),则\(h'(x)>0\),\(h(x)\)单调递增;
故\(h(x)_{min}=h(1)=e-1\),
即\(a\leq e-1\).