微积分的本质（七）：导数和极限的定义、洛必达法则

版权声明：本文为博主原创文章，如需转载，请注明出处： https://blog.csdn.net/MASILEJFOAISEGJIAE/article/details/82962857

1.导数的正式定义
在 $t$ 的位置对函数 $f(x)$ 求导：
$\frac{df}{dx}(t)=\displaystyle{\lim_{h \to 0}}\frac{f(t+h)-f(t)}{h}$

$h$ 其实等价于 $dx$ ， $dx$用来表示函数 $f$取值的具体有限小的变化量。

讨论极限，讨论的是变量逼近于0时的影响，而不是无穷小的变化量的影响。

2.极限的 $(\epsilon,\delta)$定义
函数 $f(h)=\frac{(2+h)^3-2^3}{h}$的图像如下：

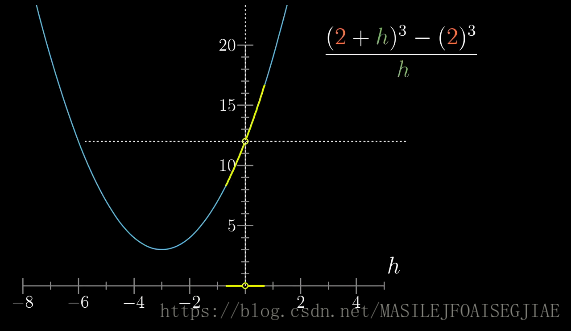
对于函数 $f(h)=\frac{(2+h)^3-2^3}{h}$，当h=0的时候，函数值变成 $\frac{0}{0}$，在这个点并没有明确的值，我们用一个空心圆来表示这个间断点。但当 $h$无限接近0的时候，函数仍然有意义，函数值逼近于12，而这个结果，和函数从哪一边逼近无关。

逼近的定义：对于x=0附近的一些取值，当取值范围在0附近不断缩小时，函数范围越来越接近12

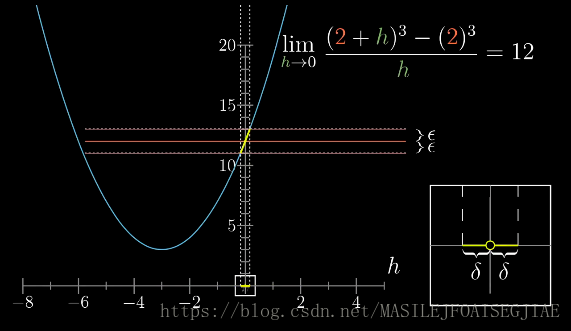
极限存在：总能在极限点附近，离这一点距离为 $\delta$的取值范围内，找到一系列取值点，使得这范围内的任一个取值点，其函数值都在到某个值的距离为 $\epsilon$的范围之内。这种情况，对任意 $\epsilon$都成立。无论 $\epsilon$多么小，总能找到与之对应的 $\delta$值。

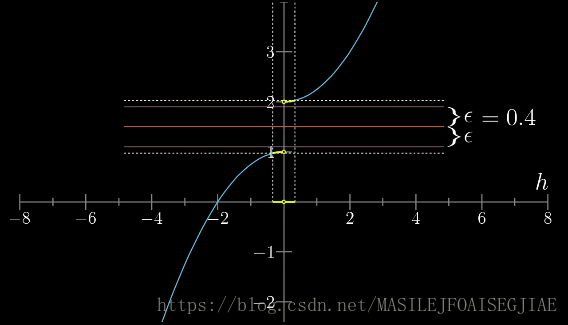
下图是一个极限不存在的一个例子：找到一个足够小的 $\epsilon$，例如0.04，无论 $\delta$多么小，对应的函数值，都不能完全位于两个 $\epsilon$构成的区间内，找不到任何可以逼近的极限值，所以极限不存在。

3.洛必达法则
引例：
如何求 $\displaystyle{\lim_{x \to 1}}\frac{\sin(\pi{x})}{x^2-1}$ ？

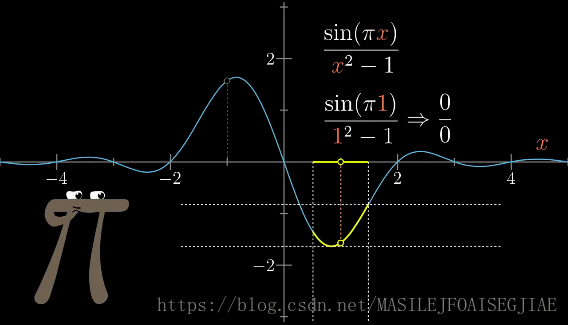
直接把1代入函数，分子和分母都是0，无法直接获得函数逼近 $x=1$的结果。

下面分别给出分子 $\sin(\pi{x})$ 和分母 $x^2-1$ 的函数图像

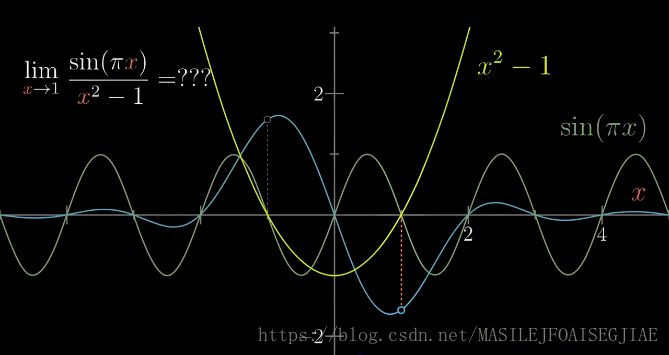
当 $x=1$时，两个函数的值都为 $0$，都穿过 $x$轴。考虑微小变化量 $dx$对函数的影响。

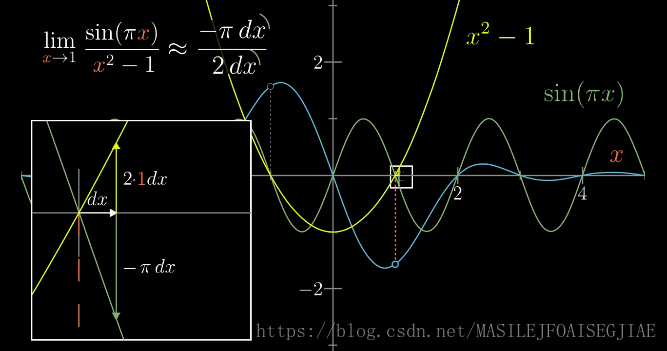
当 $x=1$时， $\sin(\pi x)$函数值的变化量为
$d(\sin(\pi x))=\cos(\pi x) \pi dx=-\pi dx$

同理得
$d(x^2-1)=2xdx=2dx$
则有
$\displaystyle{\lim_{x \to 1}}\frac{\sin(\pi{x})}{x^2-1}=\frac{-\pi dx}{2dx}=\frac{-\pi}{2}$
所以当 $x$逼近于1时，这个极限的精确值为 $\frac{-\pi}{2}$

一般地，考虑任意两个函数 $f(x)$和 $g(x)$，它们在 $x=a$处可导，且 $g(a)=f(a)=0$ ，如何计算 $\displaystyle{\lim_{x \to a}}\frac{f(x)}{g(x)}$的值？
因为 $g(a)=f(a)=0$ ，所以并不能直接计算 $\frac{f(a)}{g(a)}$的值。因此，我们要求 $x$逼近于 $a$时的极限值。
两个函数在 $x=a$处都可导，意味着在无限放大之后，他们可以被看作是直线。如下图：

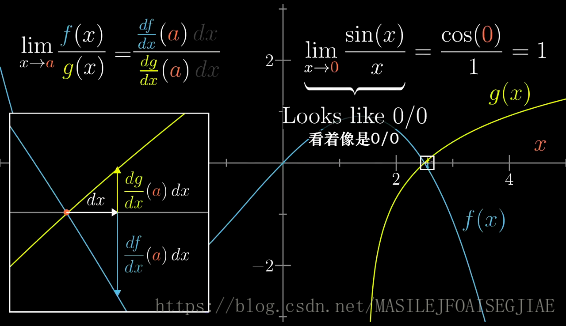
考虑一个到 $x=a$的距离为 $dx$的点，对函数 $f(x)$，该点的函数值，非常接近该点的导数值和 $dx$的乘积，即 $\frac{df}{dx}(a)dx$.
同理，对函数 $g(x)$，这个值大约是 $\frac{dg}{dx}(a)dx$.

当 $dx$越小的时候， $\frac{df}{dx}(a)dx$和 $\frac{dg}{dx}(a)dx$就越接近 $x=a$的函数值，甚至可以等同于极限的精确值，则有
$\displaystyle{\lim_{x \to a}}\frac{f(x)}{g(x)}=\frac{\frac{df}{dx}(a)dx}{\frac{dg}{dx}(a)dx}=\frac{\frac{df}{dx}(a)}{\frac{dg}{dx}(a)}$
当要计算 $\frac{0}{0}$型函数的极限的时候，可以使用这个技巧，对分子分母分别求导，并代入极限点的取值。
这一技巧就叫做洛必达法则。

回顾一开始对导数的定义：
$\frac{df}{dx}(\textcolor{red}x)=\displaystyle{\lim_{h \to 0}}\frac{f(\textcolor{red}x+h)-f(\textcolor{red}x)}{h}$
本质上就是计算 $\frac{0}{0}$型函数的极限，那是不是就可以使用洛必达法则暴力求解了呢？很遗憾，如果不知道分子的导数，则无法使用洛必达法则。因此，洛必达法则的一个应用前提就是——分子分母都可导。

参考资料： 【官方双语】微积分的本质 - 07 - 极限.