微积分：2.1导数中的中值定理

本课程来自 深度之眼，部分截图来自课程视频。
【第二章 微积分】2.1导数中的中值定理
在线LaTeX公式编辑器

任务详解：

这节课主要介绍了函数的导数，中值定理与洛必达法则等知识点。
掌握目标：
1、掌握导数的意义以及初等函数导数公式，求导法则
2、了解中值定理，洛必达法则
，泰勒公式
3、了解函数的凹凸性
4、掌握函数的极值，以及极值的充要条件
5、掌握不定积分，定积分的计算，第一第二类换元，分部积分法，牛顿莱布尼茨公式

1.函数的导数

导数的引入：

1.直线运动的速度

计算 $t_0$的瞬时速度为：
$v=\lim_{t \to t_0}\frac{f(t)-f(t_0)}{t-t_0}$
2.曲线的切线

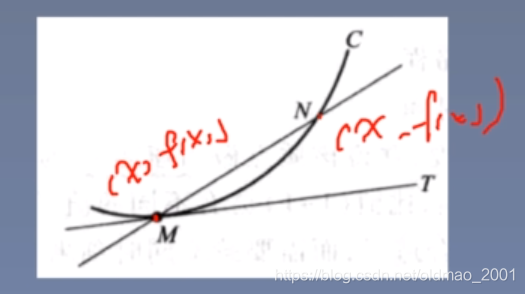
求MN两点间割线的斜率(当N无限靠近M的时候，就相当于M点切线的斜率)：
$k=\lim_{x \to x_0}\frac{f(x)-f(x_0)}{x-x_0}$

定义

定义设函数 $y=f(x)$在点 $x_0$的某个邻域内有定义，当自变量 $x$在 $x_0$处取得增量 $\Delta x$（点 $x_0+\Delta x$仍在该邻域内）时，相应地，因变量取得增量 $\Delta y= f(x_0+\Delta x）-f(x_0)$；如果 $\Delta y$与 $\Delta x$之比当 $\Delta x \to 0$时的极限存在，那么称函数 $y=f(x)$在点 $x_0$处可导，并称这个极限为函数 $y=f(x)$在点 $x_0$处的导数，记为 $f'(x_0)$，即
$f'(x_0)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$
也可记作 $y'|_{x=x_0}$, $\frac{dy}{dx}|_{x=x_0}$或 $\frac{df(x)}{dx}|_{x=x_0}$

常用函数的导数

函数 $f(x)=C（C为常数）$的导数为：0
函数 $f(x)=x^n（n\in N）$的导数为： $nx^{n-1}$
幂函数 $f(x)=x^\mu（\mu \in R）$的导数为： $\mu x^{\mu-1}$
函数 $f(x)=sinx$的导数为： $cosx$
函数 $f(x)=a^x（a>0，a\neq 1）$的导数为： $a^xlna$，特别的当 $a=e$时， $(e^x)'=ex$
函数 $f(x)=log_ax（a>0，a\neq 1）$的导数为： $\frac{1}{xlna}$，特别的当 $a=e$时， $(lnx)'={1}{x}$

定理：导数存在<==>左右导数存在且相等
例题：函数 $f(x)=|x|$在 $x=0$处的导数不存在
$\lim_{\Delta x\to 0}\frac{|x+\Delta x|-|x|}{\Delta x}=\lim_{\Delta x\to 0}\frac{|\Delta x|}{\Delta x}$
当（右极限或叫右导数） $\Delta x\to 0^+,\frac{\Delta x}{\Delta x}=1$，
当（左极限或叫左导数） $\Delta x\to 0^-,\frac{\Delta x}{\Delta x}=-1$
左右极限不相等，故导数不存在。

求导法则

$1.[u(x)\pm v(x)]'=u(x)'\pm v(x)'$
$2.[u(x) v(x)]'=u(x)' v(x)+u(x) v(x)'$
$3.\left[ \frac{u(x)}{v(x)}\right]=\frac{u(x)' v(x)-u(x) v(x)'}{v^2(x)}\quad (v(x)\neq 0)$

链式法则

如果 $u=g(x)$在点x可导，而 $y=f(u)$在点 $u=g(x)$可导，那么复合函数 $y=f[g(x)]$在点 $x$可导，且其导数为：
$\frac{dy}{dx}=f'(u)\cdot g'(x)或\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}$

高阶导数

2.中值定理与洛必达法则

拉格朗日中值定理

如果函数 $f(x)$满足
（1）在闭区间 $[a,b]$上连续；
（2）在开区间 $(a,b)$内可导，那么在 $(a,b)$内至少有一点 $(a<f<b)$，使等式
$f(b)-f(a)=f'(\xi)(b-a)$
成立.
从图像上看就是a，b两点间的曲线上，总是可以找到一个点的切线的斜率与线ab的斜率相等（二者平行） $\frac{f(b)-f(a)}{(b-a)}=f'(\xi)$

拉格朗日中值定理是柯西中值定理的一种特殊情况（就是 $F(x)=x$）。

柯西中值定理

如果函数 $f(x)$及 $F(x)$满足
（1）在闭区间 $[a,b]$上连续；
（2）在开区间 $(a,b)$内可导；
（3）对任一 $x\in (a,b),F'(x)\neq 0$，那么在 $(a,b)$内至少有一点，使等式
$\frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f'(\xi)}{F'(\xi)}$
成立。

洛必达法则

主要是用来求两个无穷小之比或两个无穷大之比的极限。
方法是：通过分子分母分别求导再求极限。
证明过程用到了柯西中值定理。