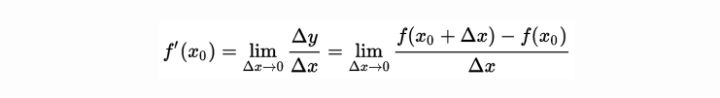导数(derivative)
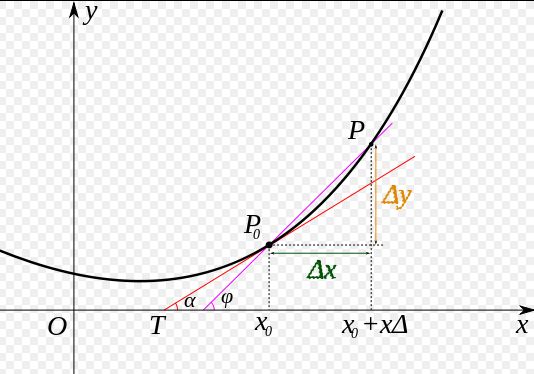
导数,是我们最早接触的一元函数中定义的,可以在 xy 平面直角坐标系中方便的观察。当 时, 处的导数就是该点的切线的斜率。
偏导数(partial derivative)
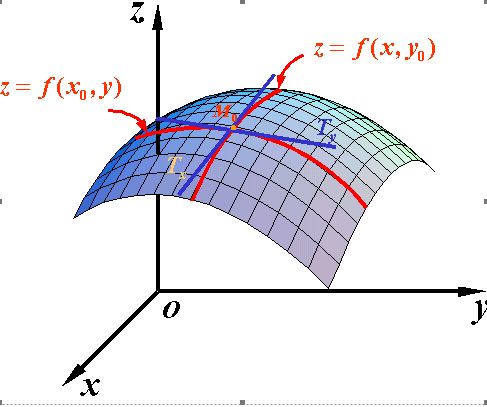
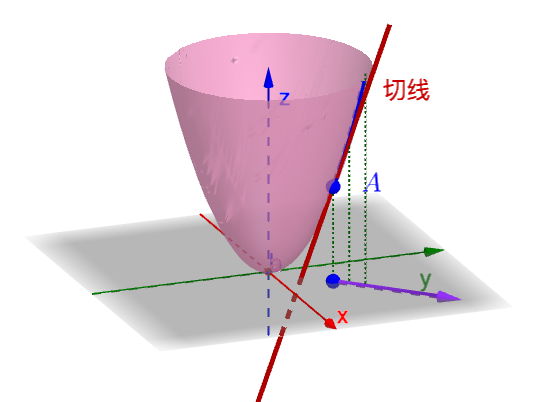
偏导数对应多元函数的情况,对于一个
元函数
,在
空间内的直角坐标系中,函数沿着某一条坐标轴方向的导数,就是偏导数。在某一点处,求
轴方向的导数,就是将其他维的数值看做常数,去截取一条曲线出来,这条曲线的导数可以用上面的导数定义求。求出来就是此点在这条轴方向上的偏导数。
方向导数 (directional derivative)
很多时候,仅仅有了坐标轴方向上的偏导数是不够的,我们还想知道任意方向上的导数。函数在任意方向上的导数就是方向导数。而空间中任意方向,是一定可以用坐标轴线性组合来表示的,这就架起了偏导数和方向导数的桥梁:
令 ,
其中, 是由偏导数定义的向量 与 我们自己找的单位方向向量 之间的夹角。
扫描二维码关注公众号,回复:
2660745 查看本文章


梯度 (gradient)
在上面的方向导数中,
- 是固定的
- 是固定的
- 唯一变化的就是
当 与 同向的时候,方向导数取得最大,此时我们定义一个向量 ,其方向就是 的方向,大小就是 的模长,我们称这个向量就是此点的梯度。沿着梯度方向,就是函数增长最快的方向,那么逆着梯度方向,自然就是函数下降最快的方向。由此,我们可以构建基于梯度的优化算法。