【机器学习的高等数学基础】导数的几何意义和物理意义、函数的可导性与连续性之间的关系、平面曲线的切线和法线、基本导数与微分表、微分中值定理，泰勒公式、弧微分、曲率、曲率半径、洛必达法则、.渐近线的求法等

机器学习的数学基础

高等数学

1.导数定义：

导数和微分的概念

2.左右导数导数的几何意义和物理意义

函数f(x)在x_0处的左、右导数分别定义为：

3.函数的可导性与连续性之间的关系

4.平面曲线的切线和法线

切线方程 :

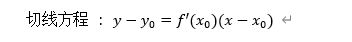
法线方程：

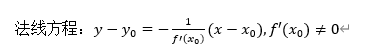
5.四则运算法则

6.基本导数与微分表

(1) y=c（常数） 则： y^’=0 dy=0
(2) y=x^α(α为实数) 则： y’=αx^(α-1) dy=αx^(α-1) dx
(3) y=a^x 则： y’=a^x lna dy=a^x lnadx 特例: (e^x)’=ex d(e^x)=ex dx
(4) y=log_a x 则：
y’=1/xlna ，dy=1/xlna dx 特例:y=lnx (lnx)’=1/x d(lnx)=1/x dx
(5) y=sinx 则：y’=cosx d(sinx)=cosxdx
(6) y=cosx 则：y’=-sinx d(cosx)=-sinxdx
(7) y=tanx 则： y^’=1/(cos2 x)=sec^2 x d(tanx)=sec^2 xdx
(8) y=cotx 则：y’=-1/(sin^2 x)=-csc^2 x d(cotx)=-csc^2 xdx
(9) y=secx 则：y’=secxtanx d(secx)=secxtanxdx
(10) y=cscx 则：y’=-cscxcotx d(cscx)=-cscxcotxdx
(11) y=arcsinx 则：y’=1/√(1-x^2 ) d(arcsinx)=1/√(1-x^2 ) dx
(12) y=arccosx 则：y’=-1/√(1-x^2 ) d(arccosx)=-1/√(1-x^2 ) dx
(13) y=arctanx 则：y’=1/(1+x^2 ) d(arctanx)=1/(1+x^2 ) dx
(14) y=arccotx 则：y’=-1/(1+x^2 ) d(arccotx)=-1/(1+x^2 ) dx
(15) y=shx 则：y’=chx d(shx)=chxdx
(16) y=chx 则：y’=shx d(chx)=shxdx

7.复合函数，反函数，隐函数以及参数方程所确定的函数的微分法

(1) 反函数的运算法则: 设y=f(x)在点x的某邻域内单调连续，在点x处可导且f’(x)≠0，则其反函数在点x所对应的y处可导，并且有dy/dx=1/(dx/dy)
(2) 复合函数的运算法则:若μ=φ(x)在点x可导,而y=f(μ)在对应点μ(μ=φ(x))可导,则复合函数y=f(φ(x))在点x可导,且y’=f’(μ)⋅φ’(x)
(3) 隐函数导数dy/dx的求法一般有三种方法：
1)方程两边对x求导，要记住y是x的函数，则y的函数是x的复合函数.例如1/y，y^2，lny，ey等均是x的复合函数. 对x求导应按复合函数连锁法则做。
2)公式法.由F(x,y)=0知 dy/dx=-(〖F’〗_x (x,y))/(〖F’〗_y (x,y)),其中，〖F’〗_x (x,y)， 〖F’〗_y (x,y)分别表示F(x,y)对x和y的偏导数。
3)利用微分形式不变性

8.常用高阶导数公式

（1）(a^x) ^((n))=ax ln^n a (a>0)  (e^x) ^((n))=e ^x
（2）(sinkx) ^((n))=kn sin(kx+n⋅π/2)
（3）(coskx) ^((n))=kn cos(kx+n⋅π/2)
（4）(x^m) ^{((n))=m(m-1)⋯(m-n+1)x}(m-n)
（5）(lnx) ^{((n))=〖(-1)〗}((n-1)) ((n-1)!)/x^n
（6）莱布尼兹公式：若u(x) ,v(x)均n阶可导，则： 〖(uv)〗^{((n))=∑_(i=0)}n▒〖c_n^i u^((i)) v^((n-i)) 〗，其中u^((0))=u，v((0))=v

9.微分中值定理，泰勒公式

Th1:(费马定理)
若函数f(x)满足条件：
(1)函数f(x)在x_0的某邻域内有定义，并且在此邻域内恒有 f(x)≤f(x_0)或f(x)≥f(x_0),
(2) f(x)在x_0处可导,则有 f’(x_0)=0
Th2:(罗尔定理)
设函数f(x)满足条件：
(1)在闭区间[a,b]上连续； (2)在(a,b)内可导；(3)f(a)=f(b)
则在(a,b)内∃一个ξ，使 f’(ξ)=0
Th3: (拉格朗日中值定理)
设函数f(x)满足条件：
(1)在[a,b]上连续；(2)在(a,b)内可导；
则在(a,b)内存在一个ξ，使 (f(b)-f(a))/(b-a)=f’(ξ)
Th4: (柯西中值定理)
设函数f(x)，g(x)满足条件：
(1) 在[a,b]上连续；(2) 在(a,b)内可导且f’(x)，g’(x)均存在，且g’(x)≠0
则在(a,b)内存在一个ξ，使 (f(b)-f(a))/(g(b)-g(a))=(f’(ξ))/(g’(ξ))

10.洛必达法则

法则Ⅰ(0/0型不定式极限)
设函数f(x),g(x)满足条件： lim┬(x→x_0 ) f(x)=0,lim┬(x→x_0 ) g(x)=0; f(x),g(x)在x_0的邻域内可导 (在x_0处可除外)且g’(x)≠0;
lim┬(x→x_0 ) f’(x)/g’(x) 存在(或∞)。
则： lim┬(x→x_0 ) f(x)/g(x) =lim┬(x→x_0 ) f’(x)/g’(x)
法则I’ (0/0型不定式极限)
设函数f(x),g(x)满足条件： lim┬(x→∞) f(x)=0,lim┬(x→∞) g(x)=0;存在一个X>0,当|x|>X时,f(x),g(x)可导,且g’(x)≠0;lim┬(x→x_0 ) f’(x)/g’(x) 存在(或∞)。
则： lim┬(x→x_0 ) f(x)/g(x) =lim┬(x→x_0 ) f’(x)/g’(x) .
法则Ⅱ(∞/∞型不定式极限)
设函数f(x),g(x)满足条件： lim┬(x→x_0 ) f(x)=∞,lim┬(x→x_0 ) g(x)=∞; f(x),g(x)在x_0 的邻域内可 导(在x_0处可除外)且g’(x)≠0;lim┬(x→x_0 ) f’(x)/g’(x) 存在(或∞)。
则： lim┬(x→x_0 ) f(x)/g(x) =lim┬(x→x_0 ) f’(x)/g’(x) .
同理法则II’(∞/∞型不定式极限)仿法则I’可写出

11.泰勒公式

设函数f(x)在点x_0处的某邻域内具有n+1阶导数，则对该邻域内异于x_0的任意点x，在x_0与x之间至少存在一个ξ，使得：
f(x)=f(x_0)+f’(x_0)(x-x_0)+1/2! f″(x_0)〖(x-x_0)〗^2+⋯ +(f^((n)) (x_0))/n! 〖(x-x_0)〗^n+R_n (x)
其中 R_n (x)=(f^((n+1)) (ξ))/((n+1)!) 〖(x-x_0)〗^(n+1)称为f(x)在点x_0处的n阶泰勒余项。
令x_0=0，则n阶泰勒公式：
f(x)=f(0)+f’(0)x+1/2! f″(0)x^2+⋯+(f((n)) (0))/n! x^n+R_n (x)……
其中 R_n (x)=(f^((n+1)) (ξ))/((n+1)!) x^(n+1)，ξ在0与x之间。(1)式称为麦克劳林公式
常用五种函数在x_0=0处的泰勒公式 ：

1. e^x=1+x+1/2! x^2+⋯+1/n! x^n+x(n+1)/((n+1)!) e^ξ
   或 =1+x+1/2! x^2+⋯+1/n! x^n+o(xn)
2. sinx=x-1/3! x^3+⋯+xn/n! sin nπ/2+x^(n+1)/(n+1)! sin⁡(ξ+(n+1)/2 π)
   或 =x-1/3! x^3+⋯+xn/n! sin nπ/2+o(x^n )
3. cosx=1-1/2! x^2+⋯+xn/n! cos nπ/2+x^(n+1)/((n+1)!) cos(ξ+(n+1)/2 π)
   或 =1-1/2! x^2+⋯+xn/n! cos nπ/2+o(x^n)
4. ln(1+x)=x-1/2 x^2+1/3 x^{3-⋯+〖(-1)〗}(n-1) x^{n/n+(〖(-1)〗}n x^{(n+1))/((n+1)〖(1+ξ)〗}(n+1) )
   或 =x-1/2 x^2+1/3 x^{3-⋯+〖(-1)〗}(n-1) x^n/n+o(xn)
5. 〖(1+x)〗^m=1+mx+(m(m-1))/2! x^2+⋯+(m(m-1)⋯(m-n+1))/n! x^n +(m(m-1)⋯(m-n+1))/((n+1)!) x^(n+1) 〖(1+ξ)〗^(m-n-1)
   或 〖(1+x)〗^m=1+mx+(m(m-1))/2! x^2+⋯+(m(m-1)⋯(m-n+1))/n! x^n+o(xn)
   
   
   

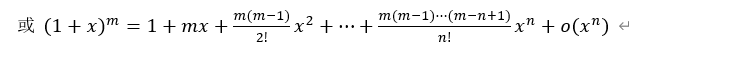
12.函数单调性的判断

Th1: 设函数f(x)在(a,b)区间内可导，如果对∀x∈(a,b)，都有f '(x)>0（或f '(x)<0），则函数f(x)在(a,b)内是单调增加的（或单调减少）。
Th2: （取极值的必要条件）设函数f(x)在x_0处可导，且在x_0处取极值，则f '(x_0)=0.
Th3: （取极值的第一充分条件）设函数f(x)在x_0的某一邻域内可微，且f '(x_0)=0（或f(x)在x_0处连续，但f '(x_0)不存在.）。
(1)若当x经过x_0时，f '(x)由“+”变“-”，则f(x_0)为极大值；
(2)若当x经过x_0时，f '(x)由“-”变“+”，则f(x_0)为极小值；
(3)若f '(x)经过x=x_0的两侧不变号，则f(x_0)不是极值。
Th4: (取极值的第二充分条件)设f(x)在点x_0处有f″(x)≠0，且f ‘(x_0)=0，则：
当f’ ‘(x_0)<0时，f(x_0)为极大值； 当f’ ‘(x_0)>0时，f(x_0)为极小值. 注：如果f’ '(x_0)0，此方法失效。

13.渐近线的求法

(1)水平渐近线
若lim┬(x→+∞) f(x)=b，或lim┬(x→-∞) f(x)=b，则y=b 称为函数y=f(x)的水平渐近线。
(2)铅直渐近线
若lim┬(x→x_0^- ) f(x)=∞，或lim┬(x→x_0^+ ) f(x)=∞，则x=x_0 称为y=f(x)的铅直渐近线。
(3)斜渐近线 若a=lim┬(x→∞) (f(x))/x, b=lim┬(x→∞) [f(x)-ax]，则 y=ax+b称为y=f(x)的斜渐近线。

14.函数凹凸性的判断

Th1: (凹凸性的判别定理）若在I上f″(x)<0（或f″(x)>0）， 则f(x)在I上是凸的（或凹的）。
Th2: (拐点的判别定理1)若在x_0处f″(x)=0，（或f″(x)不存在），当x变动经过x_0时，f″(x)变号，则(x_0,f(x_0))为拐点。
Th3: (拐点的判别定理2)设f(x)在x_0点的某邻域内有三阶导数，且f″(x)=0，f‴(x)≠0，则(x_0,f(x_0))为拐点。

15.弧微分

dS=√(1+y’^2 ) dx

16.曲率

曲线y=f(x)在点(x,y)处的曲率k=|y″|/〖(1+y’^2)〗(3⁄2) . 对于参数方程：
{■(&x=φ(t)@&y=ψ(t))┤,k=|φ’(t)ψ″(t)-φ″(t)ψ’(t)|/〖[φ’^2 (t)+ψ’^2 (t)]〗^(3⁄2)

17.曲率半径

曲线在点M处的曲率k(k≠0)与曲线在点M处的曲率半径ρ有如下关系：ρ=1/k