平稳二项随机过程模型的误差

     荷载在设计基准期T内最大值QT的概率分布

FT(x)={1-p*[1-Fi(x)]}^n

其中：将设计基准期T等分为n个相等的时段τ；

           每个时段τ内，荷载Q出现的概率为p；

           Fi(x)为荷载任意时点概率分布

当p*[1-Fi(x)]充分小，由于e^(-x)≈1-x

FT(x)≈{e^[-p*(1-Fi(x))]}^n={e^[-(1-Fi(x))]}^N≈{1-[1-Fi(x)]}^N=[Fi(x)]^N     

        上式里N=p*n，为荷载在设计基准期T内出现的平均次数

 

       当p*[1-Fi(x)]充分小，那究竟多小是充分小？

1）T=50年，Fi(x)=0.1～0.9，p=0.1，0.3，0.5，0.7，0.9，0.95，0.98，1

clc;clear;
p=[0.1 0.3 0.5 0.7 0.9 0.95 0.98 1];
for i=1:8
n=50;
Fx=[0.1:0.02:0.9];
single a;
single b;

a=(1-p(i)*(ones(1,41)-Fx)).^n;
b=Fx.^(n*p(i));
z=a-b;
y=(a-b)./a
figure;
set(gcf, 'position', [200 200 600 600]);
subplot(2,1,1);
plot(Fx,y);
xlabel('Fi(x)');
ylabel('绝对误差d');
subplot(2,1,2);
plot(Fx,z);
xlabel('Fi(x)');
ylabel('相对误差r');
end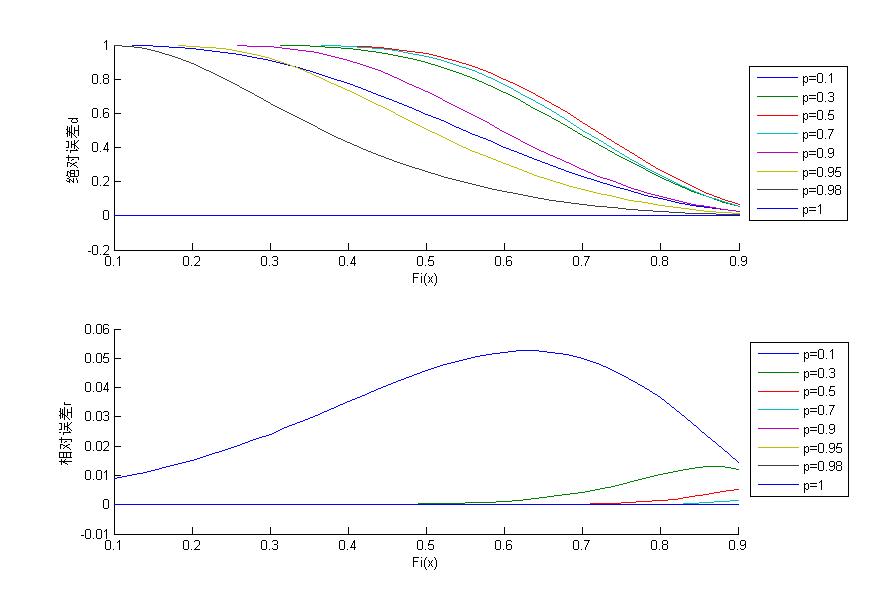

    先看绝对误差，可以看出

    每条曲线均有的共同趋势是：随着Fi(x)的增大，绝对误差逐渐减小；

    p=1，误差为0，反映了p->1，绝对误差d->0；

    p=0.5～0.9，各条绝对误差曲线呈钝角Z形，而p=0.1和p=0.3两条曲线存在一些不同；

    p=0.5～0.9，p越大，绝对误差越小，而p=0.1～0.3，p越小，绝对误差越小；

    

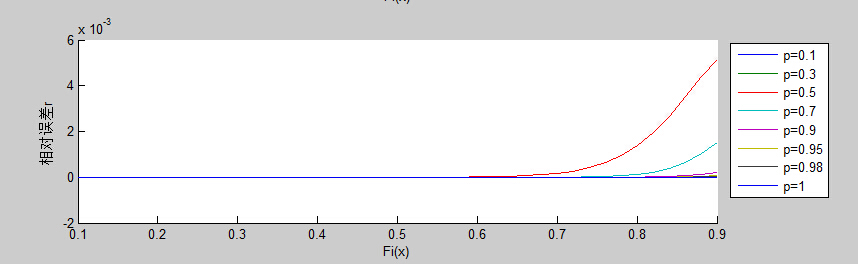
    再看相对误差，总体而言相对误差较小，仅p=0.1和0.3两条曲线误差较大，其余曲线相对误差均在1%以内，验证了平稳二项随机过程模型的正确性。

    p=0.1和0.3两条曲线相对误差先增后减，最大相对误差达到5%左右；

    Fi(x)较小时，相对误差更小，见下图去掉p=0.1和0.3的相对误差线；

    

     挖个坑，暂时没时间分析原因。