随机过程笔记(4) 二阶矩过程

---

二阶矩

• 一般来说，如果二阶矩的期望不等于0，我们会进行一下归一化操作 ( X-EX )，导出一个二阶矩为0的随机变量，方便计算以及利用各种性质

期望常用性质

这里加绝对值是针对复数的，对于实函数来说，加与不加是一样的

第一个红框

• 想要证明一个变量是二阶矩过程就证明其自相关函数是一个能用式子表达出来的
  • t²也是小于无穷的 因为只要t固定下来取值，就不是一个无穷的数，什么情况下是无穷的呢？表达式无法写的那种

第二个红框

• 可以用下一页的Jensen不等式证明，所以不用死记

第三个红框

• 有二阶矩一定有一阶矩 —》 (斯沃茨不等式 ，也就是高斯不等式证出来一阶原点矩比二阶原点矩的绝对值要小 ) 因为二阶原点矩小于正无穷了（二阶原点矩的绝对值也是小于正无穷的），所以一阶原点矩也是小于正无穷的 —》 一阶原点矩存在

• 可以用下一页的Jensen不等式证明，所以不用死记
  

• 感觉这个不是三角不等式。。不过证明过程很好理解

  • 第一行到第二行的转换的依据是：两个共轭的复数相加实际上就是实数部分的两倍，复数的实数部分又比其本身的模要小
  • 或者说第一条性质是期望自身的三角不等式，第五条性则是三角不等式套在期望里面- -

---

复二阶矩相关定理 （数字特征函数）

其实跟普通变量版本一样，就是要注意加上共轭

• 还有就是Hermit特性、非负定性（后面会用到相关性质。联想到特征函数(whose傅里叶是母函数)也具有非负定性 (R(t)有非负定性，whose傅里叶是S(w) )

下面这一页 实际上就是斯沃茨不等式 （用的也不多）

》

---

二阶矩的模和空间定义

模

实际上跟普通的模没什么区别，区别就在于这个定义有点复杂（牵扯到了期望） 仅此而已–》为甚什么牵扯到期望， 因为平时的模是针对一个数 ，而这里是一个变量 不要有畏难情绪

• 第一个红框后面会经常用到，在证明的过程中把模的形式化成这样比较方便计算

• 模的三个特性

  • 第一个是封闭性
  • 第二个是模的特性：正定、齐次、三角不等式
  • 第三个可以用Jensen不等式证（见上面）

距离和内积

距离的特性：正定性、对称性、三角不等式

• 跟模的定义一样，**内积的定义跟以前学的没有太大区别，**区别就是①由于以前是数，现在是变量，所以点乘以后还要求期望；②现在是复随机变量，所以第二个变量要取共轭

  • 自己本身的内积就是自己的模的平方 【还是没变哦】
  • 柯西不等式实际上就是斯沃茨不等式哦

随机变量的模 实际上就是自相关函数

• 自相关函数很重要

---

均方收敛

定义

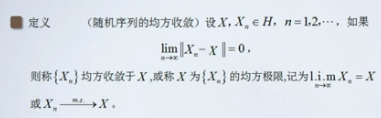
还有其他的收敛 但是本章重点关注的就是均方收敛 此处作为补充了解下即可

.

均方极限和均方收敛的关系

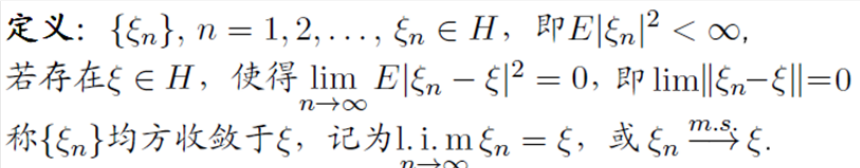
• 注意lim和l.i.m的关系 — l.i.m就代表着均方收敛，或者箭头上写m.s. ( mean square )
  而lim就是普通的趋近

证明均方收敛的两个法则

柯西准则

• 就是证这个数列是柯西列即可

洛维准则

• 内积为常数 = 该随机变量的二阶矩的平方
  
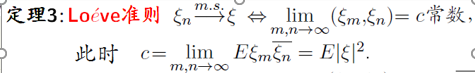
• 注意，这里的lim就是普通的lim
• 内积实际上就是 Eξ₁ξ₂，i.e. R( t1 , t2 )
• 所以证明收敛的过程中，自相关函数相当关键！！！

常见性质 （用的不多）【？？】

例题 利用两个准则证明均方收敛

定理

若存在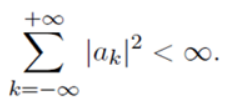，则有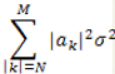（上下界都是定值，可以看作是前者的小尾巴 ）为0

---

均方连续

• 框2 实际上就是框1 的数学表达形式
• 框3 自相关函数的连续是两个维度上都要有微小变量的变化的！
• 带有均方的东西（后面的均方导数啥的也是），用的都是均方极限 ，i.e. l.i.m
• 注意，均方连续也是依靠自相关函数进行判别的
  • 所以证明连续的过程中，自相关函数相当关键！！！

补充知识

还不知道怎么用的推论

均方导数

• 二阶矩过程求导过后还是一个随机过程( 因为 t 没有消掉 )【就像分布函数求导以后的密度函数 还会是个函数！ 】，而且还是一个二阶矩过程，所以用的是l.i.m

随机变量的积分就是随机过程 ( 妙啊

高阶均方导数

广义二阶可导

普通二元函数

• 次对角线 - 主对角线

随机过程

第一个框中的 --》 随机变量 ( 随机过程的样本函数 ) 的导数还是一个随机变量（ 还是一个样本函数 --》 因为 t 并没有消掉 ）

随机过程的二阶导跟普通二元函数的二阶导是类似的，只不过此处用的是自相关函数

随机过程可导的性质

往常都有的性质

• 可导必定连续
• 导数可加线性
• 乘积导数拆分性质
  
  
  

均方可导特殊的

• 导数的E 就是 E的导数
• 导数的自相关 就是 自相关的导数

对于高阶的导数也成立

均方积分

还没看…

均方收敛的性质

＊老师说第二点实际上就是若单独收敛，则内积也收敛

推论

• 外面的极限是通常的极限
• 里面的极限是均方极限 要写成l.i.m

均方收敛准则

#加粗样式# 疑问

• 这里的依概率收敛也不懂
  

琐碎

• 马尔可夫不等式
  

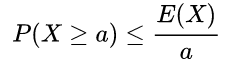
• 切比雪夫不等式
  

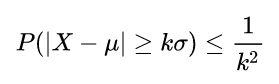
• 在这里证明了很久的均方导数之类的概念，实际上就是为了说——均方导数、均方极限等都是跟普通的导数和极限一样用就可以

• 比较重要的一个性质，均方极限和均方导数符号和期望符号是可以互换位置的