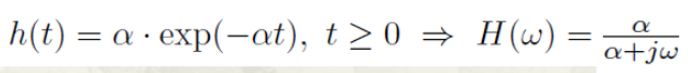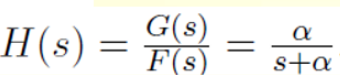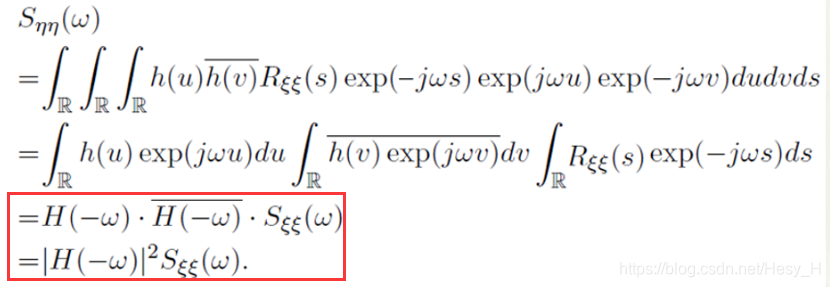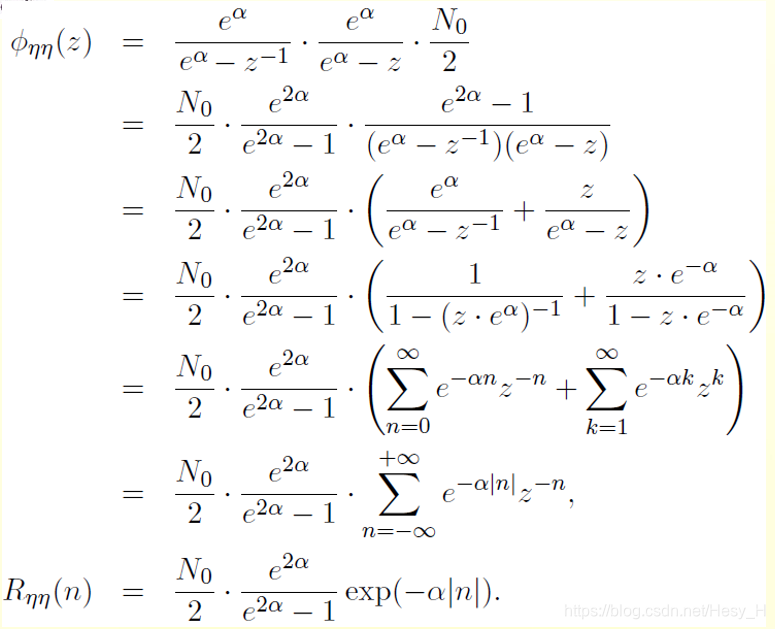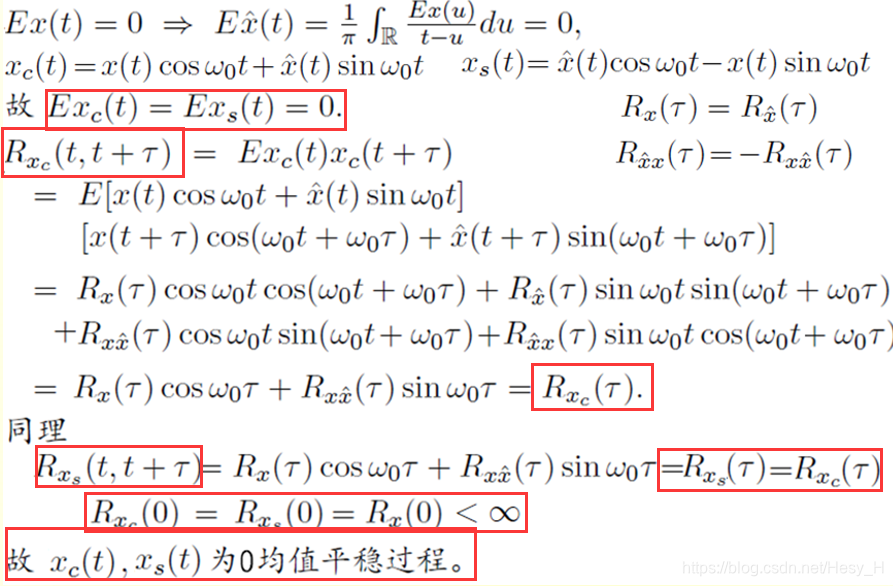随机过程笔记(7)平稳过程谱分析 2

---

系统

这个系统描述的就时某个时刻 t 的输出值g(t) 的计算方式：
取一个平均值 --》距离 t 时刻 $\tau$时间有一个信号，该信号是冲击信号的f ( $\tau$)倍的时候系统的反应( h(t, $\tau$)f( $\tau$))，对 $\tau$进行积分，就是这个均值

线性时不变系统

、
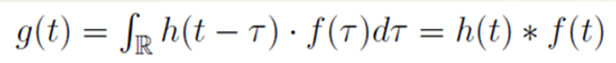特点：可以转换成输入和冲激响应函数的卷积

引例 线性时不变系统 已知输入信号的情况 揣测输出信号的情况

方法1 三个微分方程分别求解三个

方法2 时域

• 利用线性时不变系统的特性，在时域上进行计算
  • 倒数第三步 E能够放进去是因为： 从第一行可以看出来这里的平均是针对t的，其他(\tau)是常量，u和v则是引入的积分变量，属于中间量，是会被积掉的
  • 倒数第二步也是，利用u和v是中间量的特性（反正也是会被积掉的）所以最后的式子里面只有\tau没有别的变量
  • 这里将h(u)看作是另一个函数 f(u) =h(-u) ，不过这里记作h’
    • 为什么要记作-u，让三个函数的参数相加起来是一个值 —》 \tau

结论

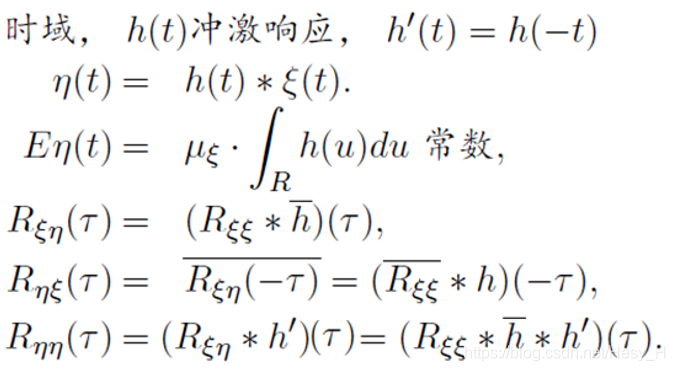
方法3 频域

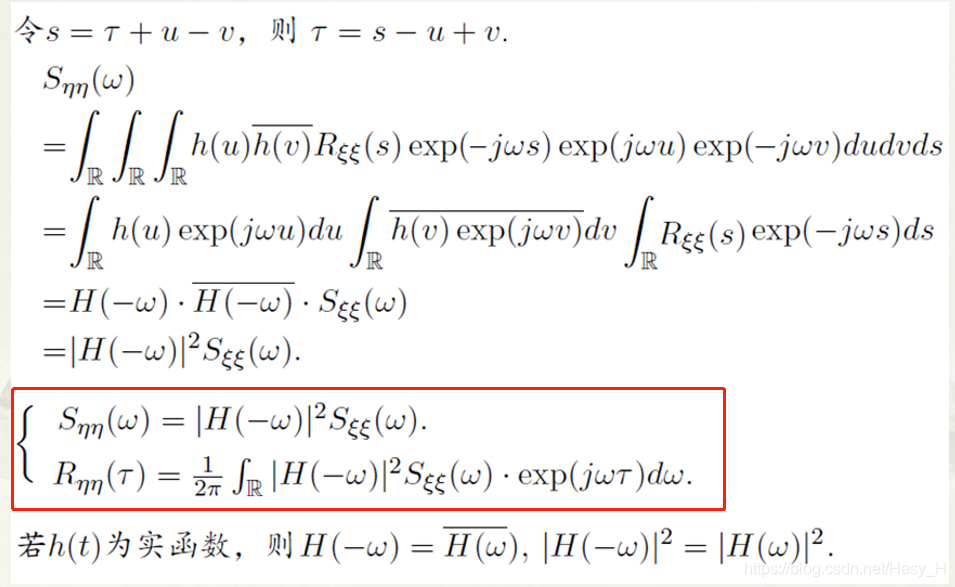
• 根据方法2推出的关系，得到输出的功率谱( S_η) 是输入的功率谱（S_ξ）的关系等式 以及 输出的自相关（R_ξ）如何用输入的功率谱( S_η )表达
• 主要思路就是

1. 找到功率谱（S）和自相关函数（R）之间的转换关系
2. 找到输出的功率谱（S_η ）和输入的功率谱（ S_ξ）之间的关系
3. 根据1、2 可以 ①从输入的自相关函数（R_ξ）得到输出的功率谱密度函数（S_η ） ② 傅里叶逆变换S_η 得到R_η

一些常见结论

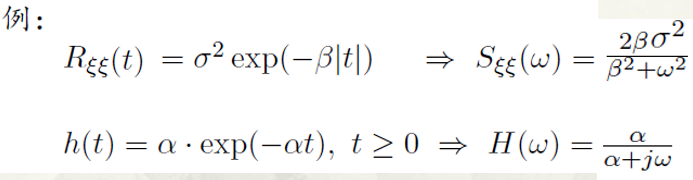
其中第一个是上次推导出来的结论，但是我们可以利用上面的结论求得：

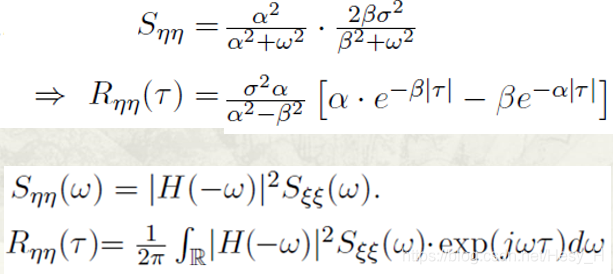
拉普拉斯Laplace变换

引入目的

线性时不变系统中，我们利用H(w)得到相关的输出的性质，那么下载就是求系统的H(w)相关性质

概念

注意，s是复数，所以这是复变函数

性质

• Lf(t)就是f(t)函数的拉普拉斯变换
  Le^atf(t)就是e^atf(t)函数的拉普拉斯变换 也就是 e^atf(t)*e^-st的单边积分

• 这里常用的一个性质就是：让各阶导数在0处取0 （零阶导就是该函数本身），这样就可以利用线性性质，将函数的导数进行拉普拉斯变换成原像

• 那个单独列出来的公式的记忆方式 ↓ ：

上文的常见结论中有傅里叶变换

这里就是 ，所以卷积里面的算子是e^-jwt的时候，分母就是加上jw；卷积里面的算子是e^-st的时候，分母就是加上s

方法论

注意，以s为变量的像是传递函数，以jw为变量的像才是频率响应（区别就是后者相当于前者衰减因子为1的情况），以t为变量原像的则是冲激响应（这是我个人对下面这个方框的勉强理解）

例子

前提：

对于之前的这个问题，看到了求导，我们可以联想到用拉普拉斯变换的线性性质进行把导数消除掉

Z变换

引入目的

之前描述的线性时不变系统都是连续的输入以及激励响应函数，这里考虑离散的

定义

• H(w)是傅里叶变换中的，H(jw)是拉普拉斯变换中的
• 双边的就是从负无穷到正无穷
  单边的就是从0到正无穷

离散时间线性时不变系统（初始0状态）

处理方法也是和之前一样有三种
第一种我们将微分改成差分 此处略去

时域

注意，这里的结论里面不再有共轭了 --》 输入是实平稳，所以第一步转换成期望的时候就咩有共轭，所以最后也没有共轭

类似的，另外一个互相关也咩有共轭，但是括号里面自变量的取负号还是要取的

频域 z域

• 注意，这里换名字了，因为这里的函数的变量不是w了，所以不是功率谱函数
• z变化可以类比傅里叶变换俩理解，只不过傅里叶变化是卷积，算子是e^-jwt，而Z变换是离散的乘积之和（注意，这里并不是离散的卷积，不要搞混），算子是z^-k

这里的算子是笔者自己的定义，大家意会就好2333

对比一下之前 连续输入情况下的

例

第一个框易得，第二个怎么来的呢？
不是利用傅里逆变换，利用的是：

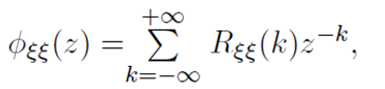
希望能把 $\phi(z)$拆成如上形式，所以就能直接用肉眼观察出R_ξξ(k)了

如下是拆分过程

简单线性时不变系统下的研究

窄带信号

物理意义

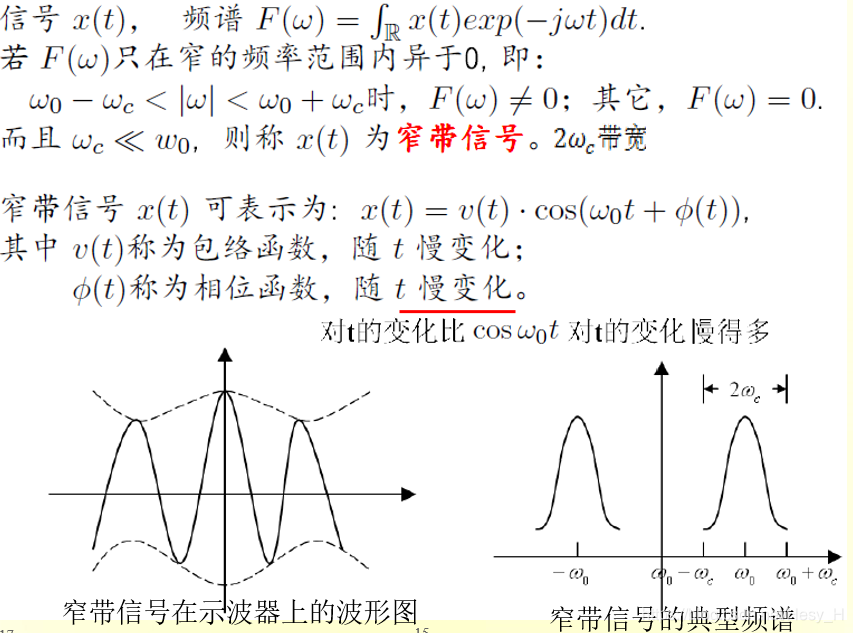
表示方法

Hilbert变换 和 线性时不变系统的关系

引入目的

可以看作一个简单线性系统的输入和输出

定义

公式记忆方法：
当x_?(t)下标( c或者s )和后面的三角函数一致的时候，符号就是负号（人生总是不完美的）【公式1】
当x_?(t)下标( c或者s )和后面的三角函数不一致的时候，符号就是＋（关一扇门，会开一扇窗）【公式2】

其中w₀是常数

至于中间方框公式的记忆方法

e^iθ=cosθ + i sinθ
x_c就是这种表示方法，i是虚部，对应x^
x_s就是由于sinθ前面乘的反而是实部( x(t) )了，所以此时要变成负号连接两项，但是cos项目还是在前面的

研究目标

目前根据前面得到的结论有：

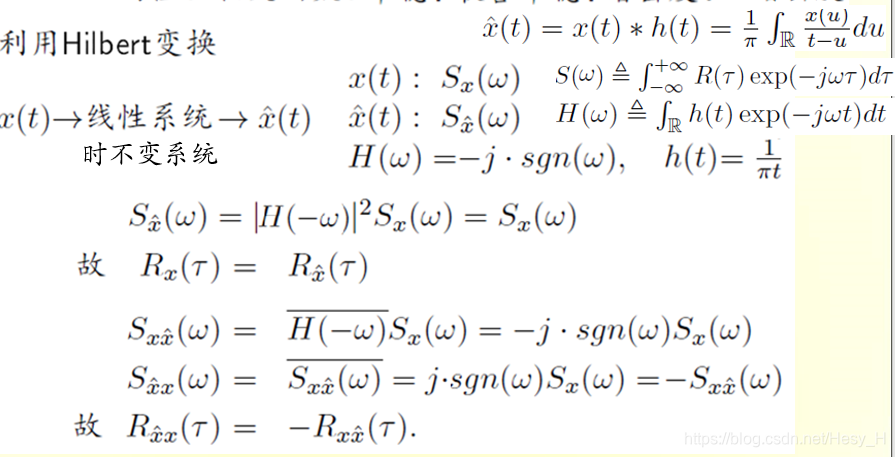
我们可以得到：

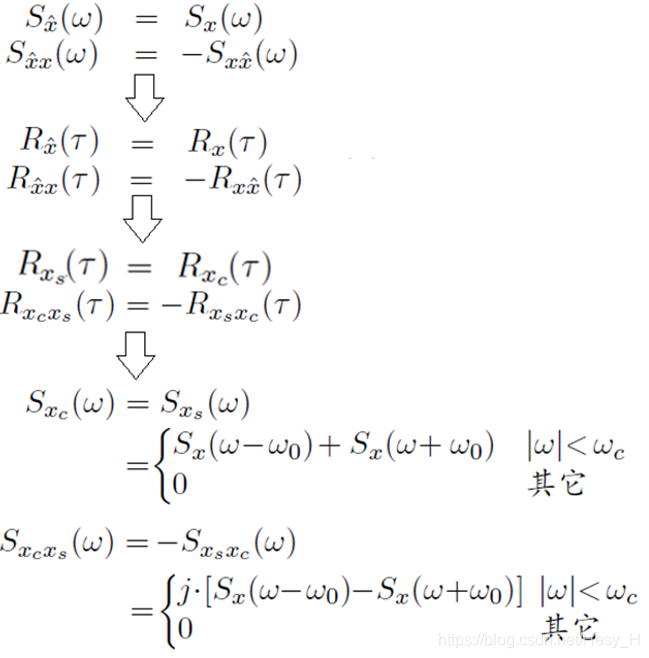
证明如下：

综上，X_s(t)和X_c(t)都是0均值的平稳过程

进一步，他们还是联合平稳的

然后我们还可以利用如上结论证明:

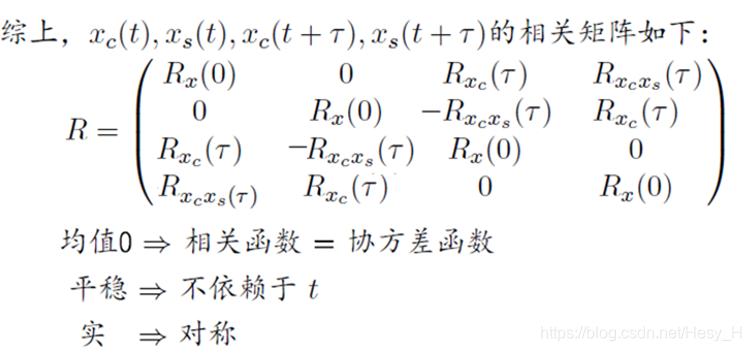
注意，我们之前研究的一直就是0均值的平稳输入过程