非平稳序列的随机分析

一、差分运算

p阶差分：前后两期序列进行一次差分—-1阶差分；对1阶差分后的序列再进行1阶差分—2阶差分；……对一个序列进行p次1阶差分—-p阶差分。
k步差分：相距 k 期的两个序列之间相减

利用函数 diff( ) 可进行差分运算

diff(x,lag= ,differences= ),lag指定步长（默认1），后一个参数指定阶数（默认1）

那如何避免过差分呢？
过差分会导致信息损失过多，估计精度低
可以根据实际情况选择p、k
1、对于有明显的线性趋势序列，1阶差分就可以实现平稳
2、有明显曲线趋势—2~3阶差分即可实现平稳
3、有固定周期的序列，需要进行步长=周期的差分
4、既有线性趋势又有周期的序列，需要做1阶差分提取趋势，再做步长=周期的差分提取周期

二、ARIMA模型

差分运算与ARMA的结合—-对差分运算后平稳的序列拟合ARMA模型

ARIMA（p,d,q）:

$$\begin{cases} Φ(B)▽^dx_t=Θ(B)ε_t \\[2ex] E(ε_t )=0,Var(ε_t )=σ^2_ε,E(ε_tε_s)=0,s≠t\\[2ex] E(x_sε_t)=0,\forall s<t \end{cases}$$
当d=1,p=q=0时为随机游走模型

性质：

$$\begin{cases} 平稳性： 当 d≠0 时，不平稳\\ 方差齐性 \end{cases}$$

建模：

对差分后平稳的序列先进行白噪声检验，若未通过则拟合ARMA模型

利用函数 arima( ) 拟合

预测：

与ARMA模型预测方法类似

疏系数模型：

原 ARIMA（p,d,q）模型中的部分自相关系数 or 移动平均部分系数缺省

利用函数 arima( ) 拟合

arima(x ,order= ,include.mean= ,method= ,transform.pars= ,fixed= )
#order:order=c(p,d,q)
#method:=“CSS-ML”为条件最小二乘与ML估计混合,默认；=“ML”为ML；=“CSS”为条件最小二乘
#transform.pars:=T系统根据order=c(p,d,q)设置的值自动完成参数估计，默认；
                =F拟合疏系数模型，不能让系统根据模型的最高阶数自动完成参数估计
#fixed：对疏系数模型指定疏系数位置

c<-read.table("D:\\Backup\\桌面\\R\\时间序列分析--基于R\\data\\file18.csv",",",header = T)
x<-ts(c$fertility,start = 1917)
par(mfrow=c(2,2))
plot(x,lwd=3,col="blue",main="时序图")
#一阶差分图
plot(diff(x),main="一阶差分图",lwd=3,col="blue")
acf(diff(x),lwd=2)
pacf(diff(x),lwd=2)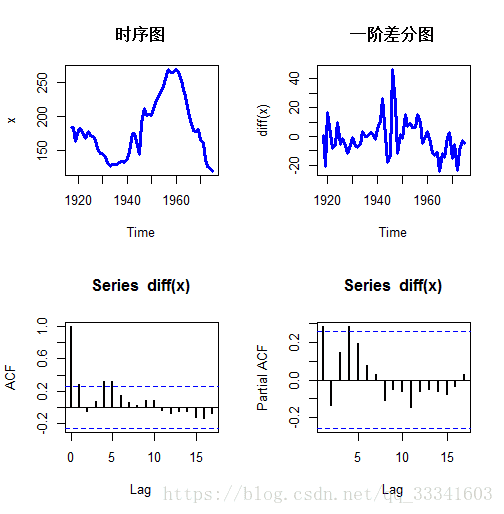

从时序图可见序列不平稳，进行一阶差分后序列平稳，从自相关图和偏自相关图可见均有截尾特征，可以拟合多个模型选取最优模型，在此拟合疏系数模型。从自相关系数来看，2、3阶=0，1、4不为0,构造1阶差分后AR（4）模型。

x.fit=arima(x,order = c(4,1,0),transform.pars = F,fixed = c(NA,0,0,NA))
x.fit
#结果如下：
Call:
arima(x = x, order = c(4, 1, 0), transform.pars = F, fixed = c(NA, 0, 0, NA))

Coefficients:
         ar1  ar2  ar3     ar4
      0.2583    0    0  0.3408
s.e.  0.1159    0    0  0.1225

sigma^2 estimated as 118.2:  log likelihood = -221,  aic = 448.01

白噪声检验

for(i in 1:2) print(Box.test(x.fit$residuals,lag = 6*i))
#结果如下：
Box-Pierce test

data:  x.fit$residuals
X-squared = 4.0909, df = 6, p-value = 0.6644


    Box-Pierce test

data:  x.fit$residuals
X-squared = 5.3742, df = 12, p-value = 0.9443

p值大于0.05，所以可认为残差序列不是白噪声序列

预测

for(i in 1:2) print(Box.test(x.fit$residuals,lag = 6*i))
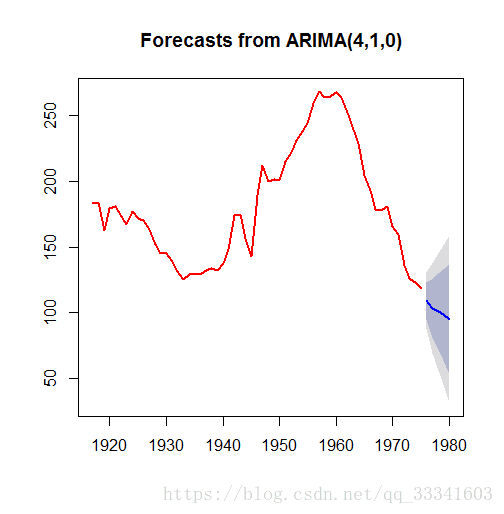
x.fore<-forecast(x.fit,h=5)
x.fore
plot(x.fore,lwd=2.5,col="red")

季节模型：

简单季节模型（即加法模型）–简单的周期步长差分即可提取序列的相关信息
乘积季节模型：趋势效应、季节效应、随机波动之间存在相互影响

arima(x ,order= ,include.mean= ,method= ,seasonal=,transform.pars= ,fixed= )
#seasonal:=list(order=c(P,D,Q),period= ),P=0,Q=0加法模型；P、Q不全为0乘法模型

c<-read.table("D:\\Backup\\桌面\\R\\时间序列分析--基于R\\data\\file20.csv",",",header = T)
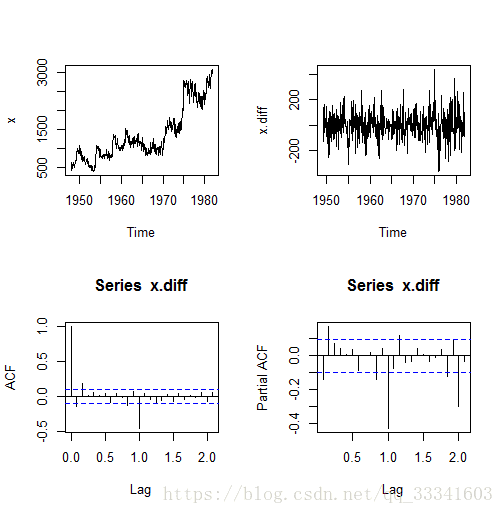
x<-ts(c$unemployment_rate,start = c(1948,1),frequency = 12)
par(mfrow=c(2,2))
plot(x)
x.diff<-diff(diff(x),12)
plot(x.diff)
acf(x.diff)
pacf(x.diff)

三、残差自回归模型

在ARIMA中，利用差分对确定性信息的提取比较充分，但是很难对模型进行直观解释。所以提出残差自回归模型，它的思想就是先对序列中的确定性信息提取，拟合相应的模型，再对模型的残差进自相关性检验，若残差存在自相关性那么再对残差拟合自回归模型。

残差的自相关检验：
DW检验要求自变量独立，所以在延迟因变量场合不适合用，需要用Durbin t和Durbin h统计量。

dw(fit,order.by= )
fit：模型
order.by:指定延迟因变量。进行DW检验时，不需要order.by

残差的自回归模型拟合
步骤与命令同ARIMA

四、异方差的性质

通过观察残差平方图看是否存在异方差。如果残差的方差在某个值附近随机波动则不存在异方差
存在异方差时，如何处理？
1、若已知异方差函数形式，则进行方差齐性变换（如对数变换）
2、否则拟合条件异方差模型

五、方差齐性变换

例如：美国短期国库券的月度收益率序列

d<-read.table("D:\\Backup\\桌面\\R\\时间序列分析--基于R\\data\\file21.csv",",",header = T)
x<-ts(d$yield_rate,start=c(1963,4),frequency = 12)
par(mfrow=c(2,2))
plot(x,main="序列值")
plot((diff(x))^2,main="差分后残差平方")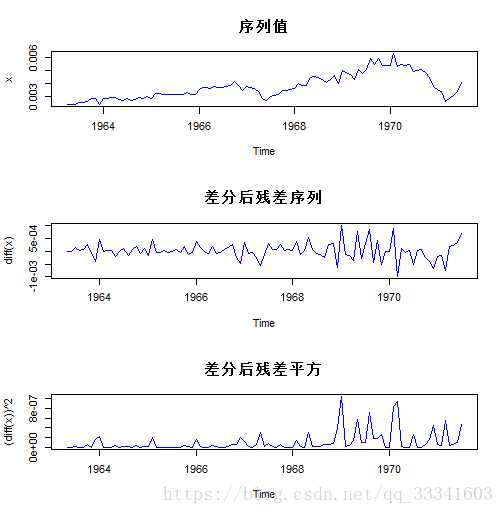

可见，1阶差分后残差序列的均值平稳但是方差有递增趋势，从残差的平方来看有异方差特性
下面进行对数变换

lnx<-log(x)
plot(lnx,main="对数序列")
plot(diff(lnx),main="对数序列进行一阶差分")
#残差白噪声检验
for(i in 1:2) print(Box.test(diff(lnx),lag = 6*i))
#白噪声检验结果：
Box-Pierce test

data:  diff(lnx)
X-squared = 3.4118, df = 6, p-value = 0.7557


    Box-Pierce test

data:  diff(lnx)
X-squared = 9.8323, df = 12, p-value = 0.6307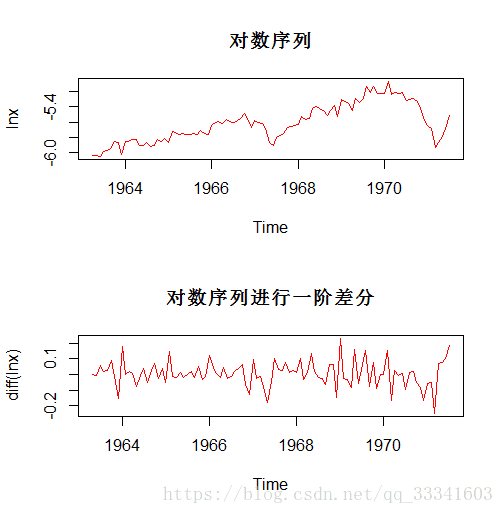

可见，对序列进行对数变换之后，残差序列显示平稳，也通过白噪声检验，说明残差具有同方差性。

六、条件异方差模型

ARCH模型

利用历史信息，得到条件方差信息

$$Var(ε_t|ε_{t-1},ε_{t-2},…)=E(ε^2_t|ε_{t-1},ε_{t-2},…)=ω+\sum_{j=1}^qλ_jε^2_{t-j}$$

集群效应：金融领域，有很多序列在大部分时间段都是平稳的，但是在某一时期，序列波动较大

ARCH模型：自回归条件异方差模型。用自回归的方法提取残差平方序列中的相关信息。ARIMA、残差自回归、确定性因素分解模型的区别是关注序列的水平拟合，而ARCH模型关注序列的波动拟合。

所以在分析一个序列时，应该关注水平和波动2个方面：

1. 先提取序列的水平相关信息
2. 分析残差序列中的波动信息
3. 1、2综合起来

拟合ARCH模型之前先进行ARCH检验，要求残差序列具有异方差性且这种异方差性是由某种自相关关系引起的。
ARCH检验：

$$\begin{cases} PortmanteauQ检验：残差平方序列的自相关性检验。用函数Box.test( )函数即可\\ LM检验：需要加载FinTS包，但现在R中已没有这个包 \end{cases}$$
利用函数garch( )拟合ARCH模型

garch(x,order= )
#order:=c(0,q)，拟合ARCH（q）模型
       =c(p,q)，拟合GARCH（p,q）模型

例如：在下面这个例子中，从时序图来看，序列没有显示非平稳特征，但某些时期波动较大，而且从方差（x^2,因为均值看做是0）来看，某些时期的方差大于期望方差，所以存在集群效应，认为序列是异方差序列

x<-ts(d$returns,start = c(1926,1),frequency = 12)
par(mfrow=c(2,1))
plot(x)
plot(x^2)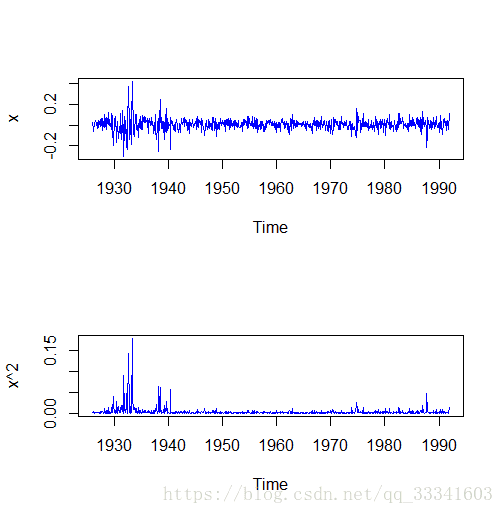

进行残差平方的自相关性检验：

for(i in 1:5) print(Box.test(x^2,lag=i))
#结果：
Box-Pierce test

data:  x^2
X-squared = 55.545, df = 1, p-value = 9.137e-14


    Box-Pierce test

data:  x^2
X-squared = 85.09, df = 2, p-value < 2.2e-16


    Box-Pierce test

data:  x^2
X-squared = 126.06, df = 3, p-value < 2.2e-16


    Box-Pierce test

data:  x^2
X-squared = 138.74, df = 4, p-value < 2.2e-16


    Box-Pierce test

data:  x^2
X-squared = 141.9, df = 5, p-value < 2.2e-16

可见残差平方序列存在自相关性
对序列拟合ARCH模型

library("tseries")
x.fit<-garch(x,order=c(0,3))
summary(x.fit)
#结果：
Call:
garch(x = x, order = c(0, 3))

Model:
GARCH(0,3)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.2420 -0.3985  0.1671  0.7501  4.4193 

Coefficient(s):
    Estimate  Std. Error  t value Pr(>|t|)    
a0 1.437e-03   6.903e-05   20.809  < 2e-16 ***
a1 7.954e-02   2.821e-02    2.820   0.0048 ** 
a2 2.231e-01   2.587e-02    8.624  < 2e-16 ***
a3 2.732e-01   4.384e-02    6.232 4.61e-10 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Diagnostic Tests:
    Jarque Bera Test

data:  Residuals
X-squared = 585.27, df = 2, p-value < 2.2e-16


    Box-Ljung test

data:  Squared.Residuals
X-squared = 8.8831e-06, df = 1, p-value = 0.9976

可见ARCH（3）模型显著，各参数也显著,得到模型：

$$E(ε^2_t|ε_{t-1},ε_{t-2},…)=0.001473+0.07954ε^2_{t-1}+0.2231ε^2_{t-2}+0.2732ε^2_{t-3}$$

GARCH模型

ARCH缺陷：因为它是用残差平方序列的q阶移动平均拟合当期异方差函数，因为移动平均模型具有q阶截尾，所以只适用于异方差函数短期自相关过程。

GARCH：适用于异方差长期自相关

在ARCH基础上，考虑了异方差函数的p阶自相关性。ARCH是GARCH的特例。

分析步骤：
当确定性信息拟合模型不能充分提取序列的信息时，残差{$ε_t$}可能具有自相关性，此时先对序列$ε_t$拟合自回归模型，再看该模型的残差序列{$v_t$}是否具有异方差性，若是则对它拟合GARCH模型。