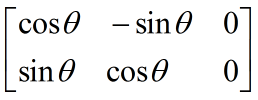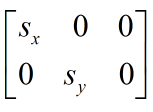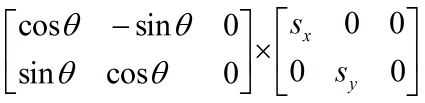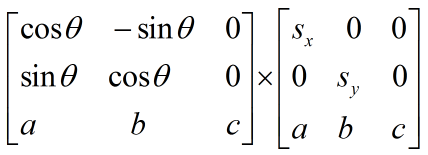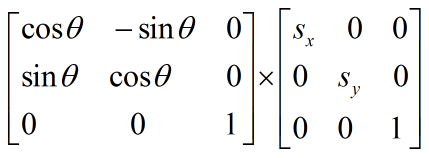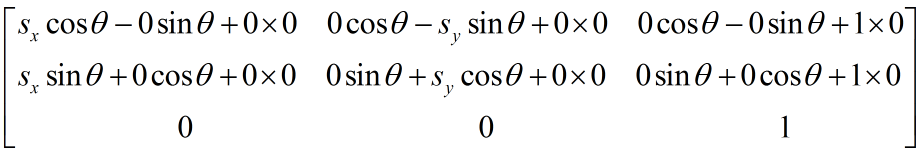好了,这次先不废话,直奔主题。
前面我们在做一些图形判断的时候,提到了两种常用的变换:缩放和旋转,它们的变换公式分别为
缩放:x'=x*scaleX,y'=y*scaleY
旋转:x'=x*cosθ-y*sinθ,y'=x*sinθ+y*cosθ
如果只是做单个变换,那么公式确实不复杂,扔到计算机上跑效率也还可以。然而,如上篇文章所言,这些变换需要逐个叠加应用到被变换的点上。此时,我们得分步计算,比如先缩放后旋转,过程如下(后面scaleX和scaleY将简写为sx和sy):
x1=x*sx,y1=y*sy
x'=x1*cosθ-y1*sinθ,y'=x1*sinθ+y1*cosθ
x'=x*sx*cosθ-y*sy*sinθ
y'=x1*sx*sinθ+y1*sy*cosθ
如果是先旋转后缩放,那我们又得重新推导一遍:
x1=x*cosθ-y*sinθ,y1=x*sinθ+y*cosθ
x'=x1*sx,y'=y1*sy
x'=x1*sx=x*cosθ*sx-y*sinθ*sx
y'=y1*sy=x*sinθ*sy+y*cosθ*sy
你会发现顺序改一下,结果都不一样了,而且推导过程也略繁琐。再者,在讲判断直线和椭圆相交的时候,例子中的椭圆还做了位置的偏移,可别小看这个平移,它也属于基本变换的一种,也能参与到上面的运算当中。(tx,ty分别代表x方向和y方向上的偏移量)
x'=x+tx
y'=y+ty
如果把平移合并进去,那么就有更多的排列方式了,而且一种变换可以不止用一次,那这是不是就意味着每种变换都要手动推导一次呢?
程序员都想偷懒,在这种情况下,可能有的朋友会想,不推导,直接分步算不就行了,比如把这个过程分两步写到代码里。
x1=x*cosθ-y*sinθ,y1=x*sinθ+y*cosθ
x'=x1*sx,y'=y1*sy
是的,这样确实没问题,但是变换多了之后,步骤多了,运行效率难免要急剧下降。对于很多应用(如3d模型的旋转等)来说,要操作的点数量特别多,假设2000个点,两步就得算4000次,3步就6000次了,跟推导后再写入代码相比,效率明显低了不少。
那么问题来了,如何能让开发效率和运行效率两者兼得?现在我们的难点就在于不同变换的公式差别较大,而且变换顺序不同还会得到不一样的结果。所以我们先来解决第一个问题:不同变换怎样统一起来。
又得啰嗦地重新列一下三种变换了:
缩放:x'=x*sx,y'=y*sy
旋转:x'=x*cosθ-y*sinθ,y'=x*sinθ+y*cosθ
平移:x'=x+tx,y'=y+ty
有点乱,所以我把变量部分的字体改成了别的颜色,这样好寻找规律。在这个过程中,只有点的坐标是变量,像旋转角度啥的都是常量,因此诸如cosθ这样的玩意儿在此处是一个常量。
是不是清晰了很多,所有计算都是变量跟常量的四则运算,其中减可以用加相反数代替,除可以用乘倒数代替,这样一来就只剩加和乘了。
既然如此,那我们就不管三七二十一,把加和乘的运算都补齐,结果如下。其中乘包括乘以x和乘以y共两个系数。
比如x方向的缩放是x'=x*scaleX,那就可以认为跟y乘了个0,再加一个0,得到:
x'=x*sx+0*y+0
类似地,我们把其它的都写出来。这次我们的重点是常量部分,所以接下来会把常量部分的字体换成其他颜色,并且放在变量前面。而变量部分则用回默认的黑色。
缩放:
x'=x*sx=sx*x+0*y+0
y'=y*sy=0*x+sy*y+0
旋转:
x'=x*cosθ-y*sinθ=cosθ*x-sinθ*y+0
y'=x*sinθ+y*cosθ=sinθ*x+cosθ*y+0
平移:
x'=x+tx=1*x+0*y+tx
y'=y+ty=0*x+1*y+ty
这样看起来就整齐多了,一个变换的结果就由6个常量来决定,于是我们可以统一写成这样:
x'=Ax*x+Bx*y+Cx
y'=Ay*x+By*y+Cy
这样的话,3种变换的区别都集中在了6个常量里面,比如平移的Bx是0,旋转的Bx=-sinθ等
我们可以按照上述公式布局出一个表,如下所示。
这样一个矩形的数阵,就是我们即将要加入史诗级玩法的——矩阵了!
现在我们把这种计算写成矩阵的形式,并且定义为乘法,就像下面这样:
可以看到,点(x,y)也被布局成了一个矩阵。
定义好了,然后我们看下矩阵各数字的位置和计算公式的关系。结果式子中的每一项都是第一个矩阵中的某个数和第二个矩阵中的某个数相乘的结果,那么我们不妨连个线。


有点乱了,所以分了两张图来连。
我们发现,这里的Cx和Cy没东西可以连,被孤立了。为了让这个形式能统一点,方便扩展,我们可以给xy那个矩阵多加一列。
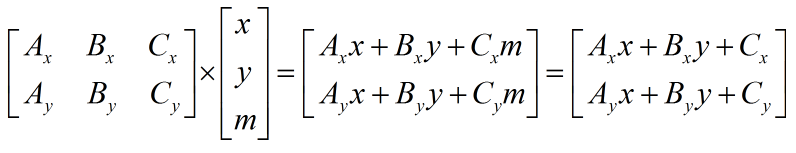
显然,让m=1就可以了。
如果用M表示变换矩阵,用p表示变换前的点,用P表示变换后的点,那么以上的变换就可以简写为M×p=P
如果用矩阵的这套理论来描述上面的变换,即先对一个点进行缩放,然后再对它进行旋转,那么整个变换就可以表示为
Mr×(Ms×p)=P
其中,Mr表示旋转矩阵,Ms表示缩放矩阵。
由前面的尝试可知,变换的先后顺序会影响最终的结果,所以矩阵乘法不满足交换律,即
Mr×(Ms×p)≠Ms×(Mr×p)
现在的矩阵还只是形式上的,计算的过程仍然没有因此而得到简化。前面提到,在这个变换过程中,点的坐标是变量,而跟点进行四则运算的系数是常量。因此p为变量,矩阵为常量。这样的话,只要能把常量部分(也就是两个矩阵)进行合并,那么在p的数量很多的时候,运算效率方面就很有优势了。
虽然矩阵不满足交换律,但结合律是满足的。
Mr×(Ms×p)=(Mr×Ms)×p
有兴趣的童鞋可以自己推导一下,写博客上一定会让大家看不下去。
现在我们把矩阵的具体式写回来。
首先,旋转变换是长这样子的:
x'=cosθ*x-sinθ*y+0
y'=sinθ*x+cosθ*y+0
所以旋转矩阵就是这个样:
类似地,缩放矩阵就是
两者相乘就是这样子:
前面转换点的时候,第二个矩阵只有一列,现在有多列了,那处理的方式就是对每一列都进行同样的操作,因此我们要像前面那样给第二个矩阵补上一行,然后由于旋转也能放到第二个矩阵上,因此所有矩阵都应该补上这一行。
那么问题来了,新补的这一行要填什么值呢?直接展开看着太繁琐了,所以我们用个单点来推导下。
为了让变换后的p点补充的行不变,确保后续运算正常,跟x和y有关的变量就不能再存在了,所以a=b=0,然后剩下的c自然就是1了。
现在可以回到两个矩阵的合并上来了。
我在三维家讲课的时候,是在白板上把展开式写出来给同事们看,而没有直接写在ppt上,因为展开后的式子太长了,ppt上看会很蛋疼。现在我想不到有什么好方法来展示这个结果,那还是直接贴出来吧。
似乎多了不少多余的运算,但是想想,点数量很多(比如3D模型)的时候,这个运算只需要做一次,而如果不用矩阵合并一下的话,就是每个点都得重复矩阵内部的四则运算,哪怕去掉了多余的项,运算量也比合并矩阵要多出来好多好多。
矩阵乘法的式子,如果编程的时候要这样具体来写,那就跟之前没什么区别了。既然矩阵是变换的统一模式,那么它必然有重用的价值。在这个研究编程的博客里,讲太多纯理论的东西估计会让大家觉得懵逼,所以下一篇,我们开始实战,第一步,先把矩阵封装成类。用什么样的语言不重要,重要的是把算法给实现出来。此处我使用JS,毕竟H5现在很火嘛,你说对不?
这篇写长了,不抒发任何的感慨,让我们下篇见,白白!