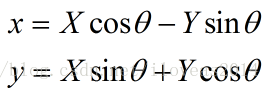这篇我们试着通过一般式来逆推回标准式。考虑到上篇估计让大家看晕。那本篇的前面我们先做个简单的事情,让xy项等于0,看看如何反推。
去掉xy项了,那我们只需要想办法去掉一次项。然后就跟标准方程没啥两样了。
在初中学习一元二次方程的时候,我们知道没一次项的方程可以直接开平方求得它的解,而包含一次项的,则可以用配方法把一次项融入到一个完全平方式中然后开方。此处我们也用类似的方法。
以x为例,有
这个1/4D^2是配方法的套路,二次项化为1之后,常数项配上一次项系数一半的平方即可。从完全平方公式可以看出这个关系来。
这个足够基础了吧?虽然我知道有的童鞋都还给老师了~~
接下来我们对上式配一下方。
这样的话一次项就等于没掉了,因为我们可以通过换元让X=x+1/2D,Y=y+1/2E,得到
这个换元只是平移变换,并不会影响曲线的形状,因此看关于新变量X,Y的方程即可判断一般式方程是啥样的。
很明显的一点,x^2和y^2项的系数并未受到一次项系数的影响,因此不包含xy项的时候,我们直接考察原方程的A和C即可。
圆的标准方程为
所以当A和C都等于1的时候,一般式方程就是圆,当然了,A=C并且不等于0也是圆,因为只要方程两端同时除以A或C即可变成如上形式。
当然了,常数项也是要看的,r^2一定要大于0,即常数部分
不过学过极限的朋友也可以说半径等于0是圆的半径无限缩小的结果,学过复数的朋友还可以认为半径小于0是半径继续收缩,往三维空间进发的结果。所以后面我不打算在诸如半径大于0这样的细节上做太多的强调,而是把目光集中在系数跟形状关系的判断上。
然后椭圆和双曲线方程中,x^2和y^2的系数都不相等,不过它们有个明显的区分
椭圆标准方程
中,x^2和y^2系数都大于0,而双曲线

的两个项为一正一负。
两个都为负数可能吗?不会,因为它们的和要等于1,如果都取负数
那x和y不管取什么数字,左边都小于等于0,没有任何点能成为曲线的一部分。不过按前面蓝色高亮部分的约定,我会对方程两边都乘以-1,然后也认为它算是椭圆的一种。
因此,A不等于C的时候,AC同号为椭圆,异号则为双曲线。
而抛物线的标准方程为

它们的特点是x^2和y^2缺失了其中一项。也就是说,当A和C有且只有其中一项为0的时候,方程就是抛物线。
当然了,这也有特殊情况,比如
y的一次项都缺失了的话,那方程就可以化作x=2或x=-2,它表示两条平行于y轴的直线,站在极限的角度上理解,它也是抛物线在y的一次项系数绝对值无限变小的结果(后面总结的时候发个图)。
如果A和C都为0,那二次项就全没了,就成了直线方程。
现在我们就来总结一下。
缺失xy项的二元二次方程
所表示的曲线仅和x^2和y^2的系数A和C有关(忽略半径等于0一类的“极限”情况),并且有:
A=C≠0时,方程为圆。
A≠C且A,C同号时,方程为椭圆。
A≠C且A,C异号时,方程为双曲线。
A≠C且A,C其中一项为0时,方程为抛物线。
A=C=0时,方程为直线。
这地方虽然说得啰嗦,但是内容还是比较简单的,对吧。就当作是为上篇缓冲一下。
现在重头戏来了,xy项若不为0,那么我们要怎么办呢?从上篇我们知道,xy可以由标准方程经过旋转后产生,那就是说,我们通过逆变换给转回去,那是有希望消灭掉xy项的,但不确定都能消掉,因为我们用待定系数法得到的方程组,其方程数量大于未知数的个数。
但无论如何,我们都试着做这个操作吧。
从标准方程转到一般方程,用的是旋转矩阵的逆矩阵,转回去,自然就是旋转矩阵的逆矩阵的逆矩阵,也就是旋转矩阵本身啦。从功能上说,把-θ改成θ即可。
我们把旋转变换代入到包含xy项的一般式中。
旋转变换为
现在我们就代入下吧,很蛋疼的,请做好心理准备!
不难看出,旋转后,一次项并未产生跟xy系数有关的变化,加上一次项在缺失xy的时候只影响位置和半径等参数的大小,不影响曲线类型,所以我在草稿纸上演算的时候会直接把一次项忽略掉。
继续展开,我们得到
很蛋疼吧,都要分行了,哈哈。不过我们现在关注的仅仅是消灭xy项,所以我们把xy项的系数提取出来,得到:
这是xy项的系数,我们要消灭掉就是要让它等于0,此处我们关心的是旋转多少度可以灭掉,因此只有θ是未知数。
三角函数有个特点,可以通过2倍角,3倍角等技巧进行降次。上式的cosθsinθ为正弦二倍角的组成部分,而(cosθ)^2-(sinθ)^2则为余弦的二倍角,于是可以这样化简:
这是一个形如asinθ+bcosθ的式子,可以运用两角和三角函数的逆变换套路进行合并。
其中新产生的字母φ不是一个变量,它是一个角度值常量,满足以下关系:
可见φ值完全可以用反三角函数表示,只不过这样太蛋疼,反倒不便于后续的讨论。
我们把这个公式代入到前面整理好的xy项系数中
其中
要让这个式子等于0,可以让C-A和B都等于0,但B=0意味着方程本身就没xy项,已经不在当前的讨论范围内,所以只能是让三角函数的部分等于0了。
要三角函数部分等于0,可以让2θ+φ=0,即θ=-φ/2
然后我们试着用ABC来建立跟-φ/2的关系。
这里要用的是三角函数的半角公式。
去掉平方的话,开方结果要根据角度的位置取不同的符号。但是这里我们不管,因为θ跟ABC已经建立了间接的关系,可能在处理的时候无需求得实际的φ值。
出来混迟早都是要还的,刚才我们懒得整理x^2和y^2的系数,但现在我们要整理了,并且得把其中的θ消掉。消掉的方法基于刚才用xy项系数等于0建立出来的等式关系,虽然不是很明朗,但估计够用了。
我们把刚才的式子搬回来。
整理可得,x^2的系数等于
因为θ=-φ/2,而这里的三角函数都是两次,所以我们用二倍角和半角公式降一下次,φ就不用再除以2了,而次数也降到了一次,可谓一举两得。
类似地,y^2的系数等于
形式上很像,然后由于现在xy项已经是0了,所以可以用回上一篇的定律来判断曲线的类型。要考察的是
这两条式子的值。
首先,我们不用考虑相等的情况,因为有xy项的一定不是圆。
然后就是符号一致的时候,方程为椭圆,可以分别让它们都大于0和都小于0建立两个方程组,或者让它们的乘积或者商大于0。
我们用后者的方法,因为相乘可以用平方差公式去掉根号。
!!!!!式子最终被化简的那一刻,我震惊了,经过一系列蛋疼的变换生成的两个如此复杂的系数,相乘结果竟然正是这个家喻户晓的一元二次方程根的判别式delta!不得不惊叹数学的美妙啊!原来各种复杂现象背后蕴含的,恰好就是大家最熟悉的东西。怪不得我国伟大的数学家范盛金(我知道有人鄙视他)也沉迷于一元三次方程求根公式的简化工作中不可自拔了,因为他也跟我一样(范盛金看到是不是要呸呸呸了),在三次方程求解过程中找到了B^2-4AC这样的一个完美的判别式。
言归正传,这个结果是一般方程旋转到消掉xy项后,x^2系数和y^2系数相乘的结果。然后对于缺xy项的方程来说,本文前面已给出了判定的方法。我们补上两系数的乘积结果。
A=C≠0时,AC>0,方程为圆。
A≠C且A,C同号时,AC>0,方程为椭圆。
A≠C且A,C异号时,AC<0,方程为双曲线。
A≠C且A,C其中一项为0时,AC=0,方程为抛物线。
A=C=0时,AC=0,方程为直线。
而旋转后的方程,AC要替换为-1/4*(B^2-4AC),然后把-1/4这个系数去掉,不等号方向改变下。接下来,我们用大家熟悉的符号Δ表示B^2-4AC,对应上面的5种情况,有如下结论:
Δ<0时,方程为圆
Δ<0时,方程为椭圆
Δ>0时,方程为双曲线
Δ=0时,方程为抛物线
Δ=0时,方程为直线
似乎出现了重叠,合并一下就是
Δ<0时,方程为圆或椭圆
Δ>0时,方程为双曲线
Δ=0时,方程为抛物线或直线
发现似乎判断尚未完成,因为有的还有两种情况,无法区分,这里我稍稍解释下。
1 圆可以理解为长短轴相等的椭圆,真要区分的话,看A和C是否相等并且B=0,满足条件则为圆,否则为椭圆。
2 双曲线其实也有特殊情况,比如x^2-y^2=0,可以对其进行因式分解,得到(x+y)(x-y)=0,所以它是两条直线,不过也可以看作是双曲线x^2-y^2=a在a趋向于0的结果(晚点看能不能上个图演示下),类似的还有x^2-3xy+2y^2=0,x^2-5xy-6y^2=0,等等。
3 直线的情况,二次项全部为0,按理说已经不归属于二元二次方程的范畴了。不过二次项不全为0也可能是直线,如前面提到的y^2-4=0,它的图像由两条平行的直线组成,但跟双曲线一样,可以理解成抛物线y^2-2px-4=0在p趋向于0的结果(有心情的时候把图补上)。
如果事先约定了一些规则,比如二次项系数不全为0,圆也归到椭圆的范畴的话,那么这个判定规则就更加简洁清晰了。
由于二元二次方程的xy项一定可以通过旋转消灭掉,所以最后给出总的结论是:
二元二次方程的一般式
一定表示圆锥曲线(特殊情况用极限来理解)。至于是哪一种曲线,可以通过判断式Δ=B^2-4AC进行判断:
Δ<0时,方程为椭圆(包括正圆)
Δ>0时,方程为双曲线
Δ=0时,方程为抛物线
现在,我们对二元二次方程的图像已经了如指掌了。比如连载十五中提到的二元二次方程
它的Δ=(-5)^2-4*2*3=1>0,因此它是一条双曲线。
在求解方程的时候,我们也可以通过诸如旋转等的变形对消元过程进行简化,让编程求解更为容易!
不过下一篇我不会马上给大家讲解方程求解。在计算机中,大家绘图经常用到的曲线往往不是椭圆,抛物线这些,而是一种有美学特征的贝塞尔曲线。所以我打算再跟大家研究下贝塞尔曲线。
有人说,二次贝塞尔曲线就是抛物线,不过当年我是坚决否定这一说法,因为虽然抛物线和二次贝塞尔曲线形式上都是y=ax^2+bx+c,但这一表达式在抛物线中是自变量和因变量的关系,而在二次贝塞尔曲线中则是变量和参数的关系。然而现在我们学习了矩阵,那有没有可能通过旋转等的矩阵变换,把二次贝塞尔曲线转换为抛物线呢?下一篇我们一起探讨这个问题,敬请期待!