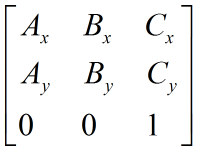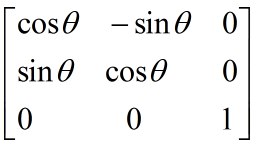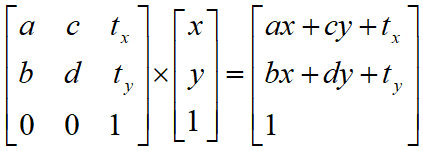在偏向计算机领域的博客上讲纯理论的东西始终有点不接地气,那就还是用代码实战一下吧。此时我的语言选择困难症开始发作,不知道用啥语言好,用我最熟悉的AS吧,会被喷,用我不熟悉的C++吧,也会被喷。C#,java啥的,对环境的依赖有点大。对于这种纯算法的教程,我不希望开发环境成为大家前进的绊脚石。所以最终就如上文所言,选择了目前很火但是开发环境依赖又很低的H5(也就是JS啦),不介意没代码提示的甚至可以用记事本敲完然后扔浏览器跑,很方便了有木有!反正吧,想用其他语言的,移植过去也不难,除非你用的是机器或者汇编。
先把上篇用到的图片放出来,我们照着实现。
ps:最后一行固定为0,0,1,理论上不予修改,但对于3D变换矩阵,最后一行是可修改的,它要控制齐次坐标,实现透视变换等功能的计算。
其中,cx和cy具有典型的平移特征,只有平移的时候用到,所以一般改名为tx和ty,意为translateX和translateY,接着只剩4个变量了,用ax,ay,bx,by似乎跟业界有点不吻合,那我也照着他们的做法改成a,b,c,d
问题来了,ax和by都有典型的缩放特征啊,为什么不改成sx和sy呢?这是因为旋转也用到了这两个变量:
最后,变量名就改成这样:
现在,我们就用比较恶心的function法来创建矩阵类了。
function Matrix(a, b, c, d, tx, ty) {
this.a = isNaN(a) ? 1 : a;
this.b = isNaN(b) ? 0 : b;
this.c = isNaN(c) ? 0 : c;
this.d = isNaN(d) ? 1 : d;
this.tx = isNaN(tx) ? 0 : tx;
this.ty = isNaN(ty) ? 0 : ty;
}这个看起来是方法的东西实际上可以当作类来使用,可以new它出来。可选参数的做法没有,只能用这种判断的方式实现。
有没发现,矩阵中的默认值有的是0,有的是1,这是怎么来的呢?下面让我们把矩阵乘法的结果套进去一下看看。
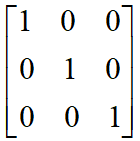
按照人类的思维习惯,一个初始被创建的矩阵应该不包含任何变换,也就是说,变换前后的结果要相等,即:
ax+cy+tx=x
bx+dy+ty=y
可见,a=1,c=0,tx=0,b=0,d=1,ty=0即可让以上两等式恒成立。
1x+0y+0=x
0x+1y+0=y
也就是说,初始的矩阵长这个样子。
这个矩阵的特点是行数和列数相等(这样的矩阵叫方阵),并且左上到右下对角线上的元素等于1,其它元素为0。事实上,对于任意大小的方阵,主对角线元素为1,其它元素为0都可以使变换前后的结果一致,这样的矩阵称作单位矩阵。在研究变换的时候,我们可以在单位矩阵的基础上,通过跟单位矩阵的差异进行分析。
知道了单位矩阵和初始数值以后,我们就来着手实现最常用的变换——乘法了。
乘法的运算公式如下:
写到代码上就是这个样子:
/**
* 跟指定矩阵相乘,并返回一个新矩阵
* @param matrix 要跟当前矩阵相乘的矩阵对象
* @return 相乘后的结果
*
**/
function multiply(matrix) {
var newMatrix = new Matrix();
newMatrix.a = matrix.a * this.a + matrix.c * this.b;
newMatrix.b = matrix.b * this.a + matrix.d * this.b;
newMatrix.c = matrix.a * this.c + matrix.c * this.d;
newMatrix.d = matrix.b * this.c + matrix.d * this.d;
newMatrix.tx = matrix.a * this.tx + matrix.c * this.ty + matrix.tx;
newMatrix.ty = matrix.b * this.tx + matrix.d * this.ty + matrix.ty;
return newMatrix;
}
this.multiply = multiply;以上代码请写入到function matrix的函数体内,本文下面的代码都按此操作。this.multiply=multiply一句是把类中的方法公有化的一个手段,有点奇葩。另外,js不支持运算符重载也是一个蛋疼之处。
大家有没发现,参数被我放到了公式左边的矩阵上,而当前矩阵则在右边。这是矩阵乘法的规矩,默认用的是左乘,而且变换一个点也是把矩阵放在点的左边。
此法生成一个新的矩阵,并没有对原矩阵的数据进行修改,实际应用中可能需要直接修改原始矩阵,那我们可以这样:
myMatrix = myMatrix.multiply(matrix); //左乘
myMatrix = matrix.multiply(myMatrix); //右乘
此法可以实现创建副本和修改数据的切换,不好的地方是myMatrix的引用被更改了,为此,我们再封装两个方法:
/**
* 矩阵左乘,会修改当前矩阵的数据
* @param matrix 要跟当前矩阵相乘的矩阵对象
*
**/
function append(matrix) {
var newMatrix = multiply(matrix);
this.copyFrom(newMatrix);
}
this.append = append;
/**
* 矩阵左乘,会修改当前矩阵的数据
* @param matrix 要跟当前矩阵相乘的矩阵对象
*
**/
function prepend(matrix) {
var newMatrix = matrix.multiply(this);
this.copyFrom(newMatrix);
}
this.prepend = prepend;
/**
* 从指定矩阵中复制数据
* @param matrix 被复制的源
*
**/
function copyFrom(matrix) {
this.a = matrix.a;
this.b = matrix.b;
this.c = matrix.c;
this.d = matrix.d;
this.tx = matrix.tx;
this.ty = matrix.ty;
}
this.copyFrom = copyFrom;
this.a = matrix.a;
this.b = matrix.b;
this.c = matrix.c;
this.d = matrix.d;
this.tx = matrix.tx;
this.ty = matrix.ty;
}
this.copyFrom = copyFrom;由于要复制的变量较多,所以我封装了个copyFrom的方法。
有复制进来也应该有个复制出去的方法,似乎大家都喜欢用clone的方式,那我也照着这套路来。
/**
* 返回当前矩阵的一个副本
*
**/
function clone() {
return new Matrix(this.a, this.b, this.c, this.d, this.tx, this.ty);
}
this.clone = clone;有了矩阵合并以后,下一个就是矩阵与点的相乘。
/**
* 当前矩阵对一个点进行转换,并返回新的点对象
* @param 要被转换的点
* @return 转换后的结果
**/
function transformPoint(p) {
var newPoint = new Point();
newPoint.x = this.a * p.x + this.c * p.y + this.tx;
newPoint.y = this.b * p.x + this.d * p.y + this.ty;
return newPoint;
}
this.transformPoint = transformPoint;这地方我建立了一个Point对象,对于js来说,换成Object也无所谓,不过为了可读性,我们还是乖乖地建一个Point类吧。
这个代码就不要放到function matrix的函数体内哦。
function Point(x, y) {
this.x = isNaN(x) ? 0 : x;
this.y = isNaN(y) ? 0 : y;
}至此,矩阵最基本的功能算是完成了,但是好像没有缩放旋转平移这些功能啊。没错,这些已经是针对具体应用场合的功能了,而非最底层,最抽象的算法。这样下来,大家是不是觉得矩阵其实很简单呢?
看到这里,不知道有没人觉得被骗了,想吐槽我。这明明是最基础的矩阵数学知识,何来什么史诗级玩法?!屎诗级玩法还差不多。如果你真有此等感受,那我先得灰常感谢你,至少你坚持读到了最后,没有读到中途甚至是刚打开就关掉了这篇文章。这个系列连载到第6篇了,其套路是先从轻量的史诗级玩法(直线椭圆相交判断)切入,然后拓展出矩阵的所有基础知识,最后等这套体系完善了再推出重度的史诗级玩法,这几篇仅仅是个过渡,谁能跨过这道坎,谁将是最后的赢家!
这篇写完,下篇补上常用变换后,就可以实现45度地图的效果,届时大家就能看到实实在在的视觉元素了。