发完上一篇文章之后，我的积极性突然被打击了下。在相关文章列表中，我找到了一个自己之前没听过的词语——影射几何。度娘告诉我，这门学科跟我所谓的“史诗级玩法”似乎有共通之处。也就是说，我拿来装逼的这玩意儿，不过是别人几百年前就玩烂了的一件玩具而已。但无论如何，我在三维家讲课，不少同事仍然表示收获颇丰，所以我选择了坚持。
判断点与图形的关系，已经是老生常谈的话题了。矩形和圆可谓是最Low的两种图形，究其原因，是其具备了太多基础几何的特性（解析几何以前所学习的教科书内容我都给归到基础几何的范畴），一些方式特殊并且难度很低的技巧即可把大部分实际问题给完美解决掉。
技术狂人重点关注的，往往是多边形的碰撞检测。它不仅应用广泛（游戏里各种复杂的图形都会用多边形近似表示），而且有深挖的空间（比如含洞，含岛，缠绕型多边形，都蕴含着各种高深的学问）。再者，多边形碰撞的效率优化也够大神们玩足几年了。
而我写的教程则把重点放到了矩阵的奇葩应用上。为了让大家在理解的过程中有个平缓的过渡，我就先从最简单的圆和矩形开始（上篇讲的就是圆）。讲课的时候，我是这篇文章和上一篇都安排到了同一节课上，但阅读博客的时间跟上课时间不一样。现在这个年代的读者大多都在利用碎片化的时间进行学习，所以我分成了两篇。
废话太多了，转入正题。
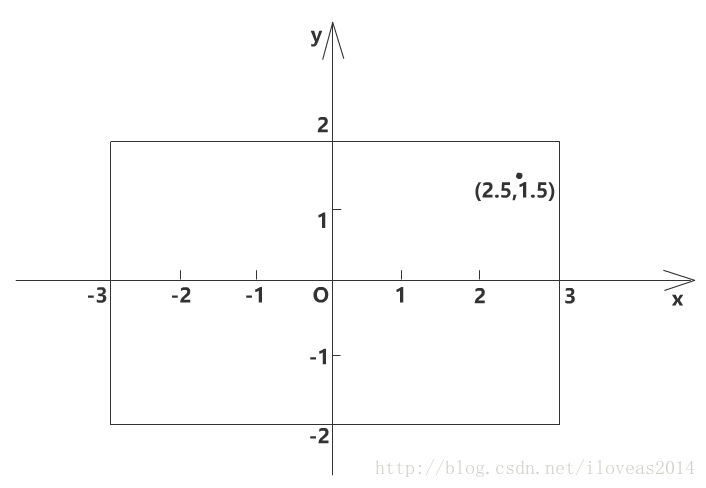
那么，如果矩形被旋转了呢？比如30度那样。
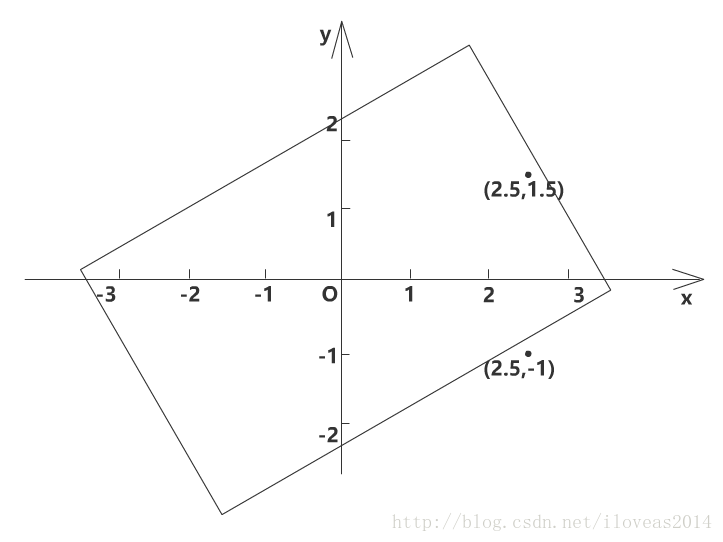
如果你理解了上一篇的套路，那我相信你已经猜到我接下来要怎么做了， 就是矩形和要被判断的点一起旋转-30度，让矩形还原到旋转前的状态。
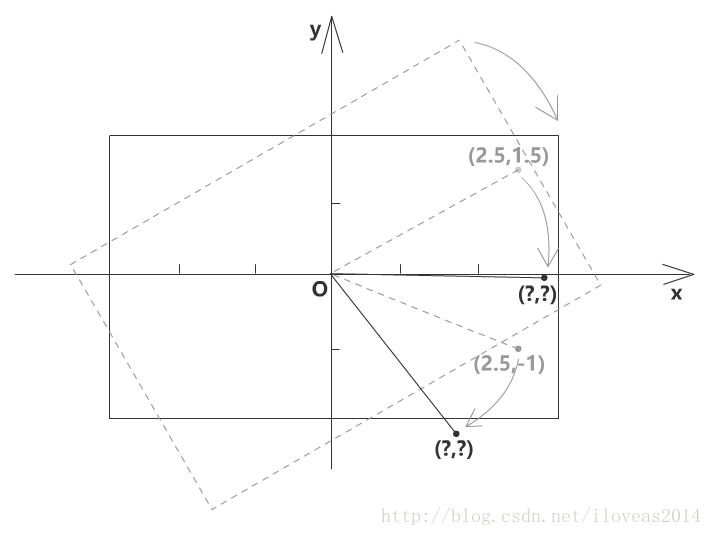
旋转完成，就可以用回最初的简单方法，判断坐标的范围。所以剩下来的问题只差如何求出被判断点旋转-30度之后的坐标了。
旋转角度跟平面坐标的关系几乎都基于三角函数（也有大神喜欢玩向量），现在我们也用类似的方法。
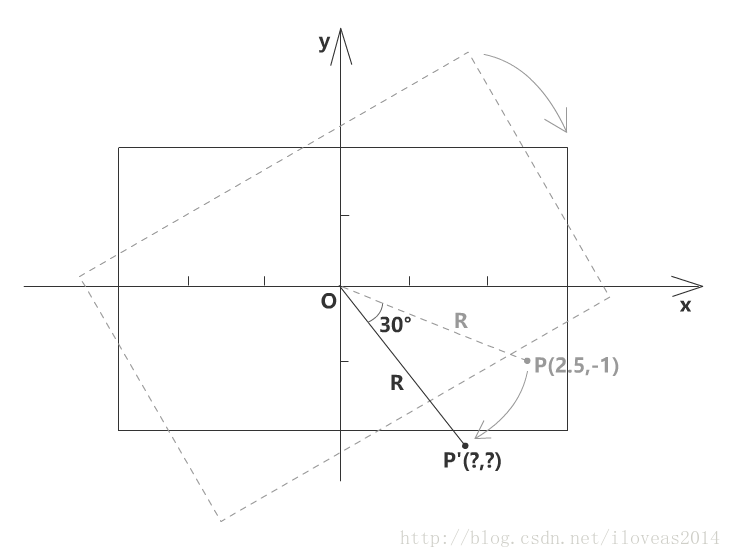
R是可以根据勾股定理算出来的，但我们不急着算，因为这里还涉及角度。
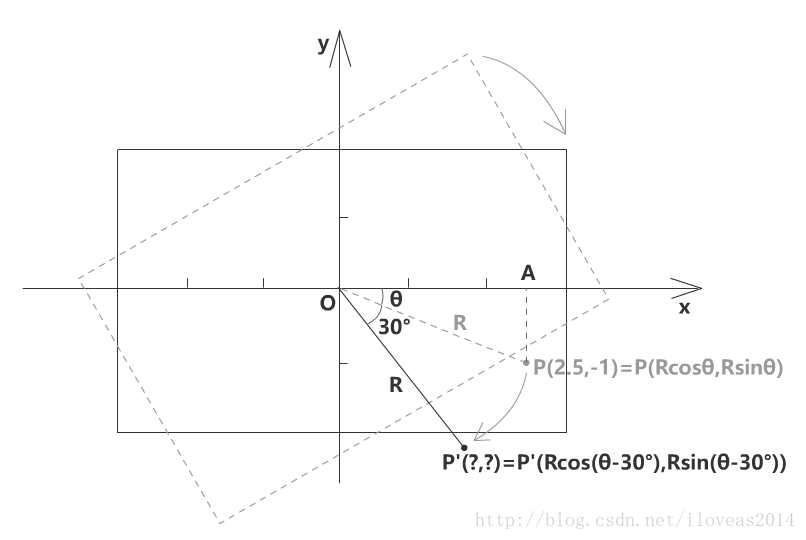
在直角三角形OAP中，根据三角函数的定义，有OA/OP=cosθ，即x/R=cosθ，所以x可以用Rcosθ代替，类似地，P的y坐标就等于Rsinθ，而P'也不难推导出来了，如上图所示。
从这个式子来看，要解出R和θ才能代入计算。但实际上三角函数部分可以展开。代入两角和差三角函数公式就能得到
Rsin( θ-30°)=Rsinθcos30°-Rcosθsin30°
不懂得两角和差三角函数的朋友可以自行百度，以前我讲课的时候还把这个当常识了，却没想到还真的有人没学过或者还给了老师
，所以有一次我还特地讲了一节专门推导两角和差三角函数的课（有录视频的，有需要的我可以发网盘地址到这儿），这里就懒得再展开了。
Rcos( θ-30°) =Rcosθcos30°+Rsinθsin30°= xcos30°+ysin30°
Rsin(θ-30°)=Rsinsθcos30°-Rcosθsin30°=ycos30°-xsin30°
把x=2.5，y=-1代入，得到新坐标
Y=ycos30°-xsin30°=-2.117
旋转后的x在-3到3之间，但y不在-2到2之间，所以判断出来了(2.5,-1)这个点不在旋转了30度的矩形内。
X=xcos30°+ysin30°=2.915
Y=ycos30°-xsin30°=0.049
x在-3到3之间，y在-2到2之间，因此(2.5,1.5)这个点在旋转了30度的矩形内。
今天这篇文章，教科书的味道似乎浓了点，但是旋转的套路却又是矩阵变换的一种。因此说穿了，所谓的矩阵史诗级玩法，无非是中学数学的基因重组的结果。
