一 行列式 方阵 矩阵的基本概念
略
二 矩阵的转置、逆、秩
-
矩阵的转置就是将矩阵中的元素进行行列对换
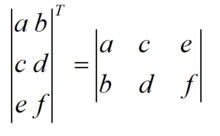
-
矩阵的逆
设A是数域上的一个n阶矩阵,若在相同数域上存在另一个n阶矩阵B,使得: AB=BA=E ,则我们称B是A的逆矩阵,而A则被称为可逆矩阵。注:E为单位矩阵。

如何求矩阵的逆:1 初等变换法
2 伴随矩阵法 -
矩阵的秩
矩阵的秩是由向量组的秩引申而来
设A是一组向量,定义A的极大无关组中向量的个数为A的秩。通常表示为r(A),或rank A。
一些重要结论 -
由定义直接可得n阶可逆矩阵的秩为n,通常又将可逆矩阵称为满秩矩阵, det(A)≠0;不满秩矩阵就是奇异矩阵,det(A)=0。
-
矩阵的行秩,列秩,秩都相等。
-
初等变换不改变矩阵的秩。
-
矩阵的乘积的秩Rab<=min{Ra,Rb}。
三 矩阵的对称性、正交性
-
矩阵的对称性:对称矩阵(Symmetric Matrices)是指元素以主对角线为对称轴对应相等的矩阵。
即满足的AT=A的矩阵。 -
矩阵的正交性:如果AAT=E(E为单位矩阵,AT表示“矩阵A的转置矩阵”)或ATA=E,则n阶实矩阵A称为正交矩阵。
由矩阵的逆和正交性可知 如果一个矩阵是正交矩阵,则 AT = A-1.
四 矩阵变换与线性变换与线性映射
矩阵变换是线性变换
线性变换是线性映射
。。。
五 矩阵的特征值、特征向量
- 矩阵的特征值和特征向量
如果一个非零向量v是方阵A的特征向量,将一定可以表示成下面形式,而λ是特征向量v对应的特征值:
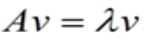
- 如何求矩阵的特征值和特征向量?
https://blog.csdn.net/Yolandera/article/details/83993828 - 特征值和特征向量的物理含义?
https://www.matongxue.com/madocs/228.html
顾名思义,特征值和特征向量表达了一个线性变换的特征。在物理意义上,一个高维空间的线性变换可以想象是在对一个向量在各个方向上进行了不同程度的变换,而特征向量之间是线性无关的,它们对应了最主要的变换方向,同时特征值表达了相应的变换程度。
具体的说,求特征向量,就是把矩阵A所代表的空间进行正交分解,使得A的向量集合可以表示为每个向量a在各个特征向量上的投影长度。我们通常求特征值和特征向量即为求出这个矩阵能使哪些向量只发生拉伸,而方向不发生变化,观察其发生拉伸的程度。这样做的意义在于,看清一个矩阵在哪些方面能产生最大的分散度(scatter),减少重叠,意味着更多的信息被保留下来。
六 矩阵相似和对角化
- 对角化矩阵的概念
可对角化矩阵是线性代数和矩阵论中重要的一类矩阵。如果一个方块矩阵 A 相似于对角矩阵,也就是说,如果存在一个可逆矩阵 P 使得 P−1AP 是对角矩阵,则它就被称为可对角化的。 - 对角化矩阵的好处
它们的特征值和特征向量是已知的,并通过简单的提升对角元素到同样的幂来把一个矩阵提升为它的幂。 - 矩阵可对角化的条件?
。。。
七 矩阵分解