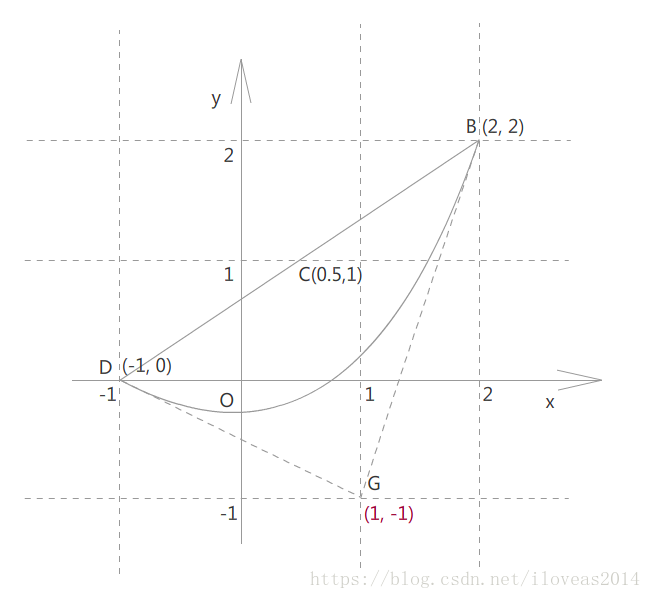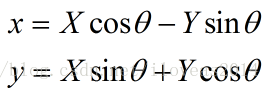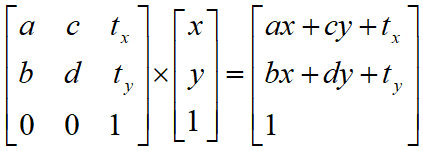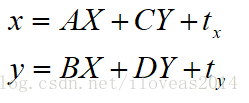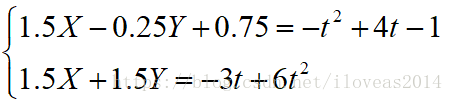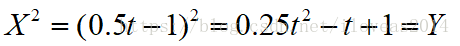在讲解砖块铺贴的时候,我们先用基础的旋转缩放等变换组合出了45度地图铺贴的变换矩阵。然后发现针对性太强,换成别的角度就很不好算了。接着改成了用基向量进行推导的方法。
然后到二元二次方程,虽然我们可以通过旋转的方法消灭掉xy项从而判断出方程对应的曲线类型,但过程过于繁琐,表达式太长,处理起来也很不方便,如果还要进行求交而不局限于判断类型,那么用前面的旋转法,演算就更加麻烦了。
既然在铺贴的实现中,基向量矩阵优于旋转矩阵,那么在转换二元二次方程的时候,是否也可以用基向量来简化呢?
然而我们发现,二元二次方程中的系数,其几何意义并不明显,光判断类型就要计算B^2-4AC,至于旋转角度,偏移量这些,恐怕就更加复杂了。
不过,二次贝塞尔曲线的方程却有特别明显的几何意义,建立起来的数据全部是直接的点坐标。
既然如此,那我们不妨用基向量直接对二次贝塞尔曲线特有的方程进行转换,反正上篇已经证明了它的本质是抛物线。
砖块铺贴我们用网格来构建基向量,那么贝塞尔这种曲线我们怎样来生成基向量呢?
实际上,坐标系本身就可以看作网格,把刻度线延长即可生成。
emmm....理工科的学生应该会似曾相识吧,实验课用到的坐标纸,嘿嘿。
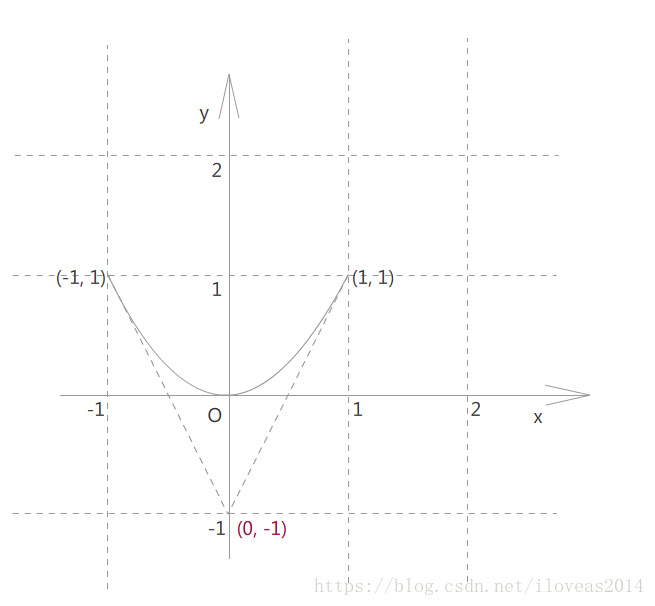
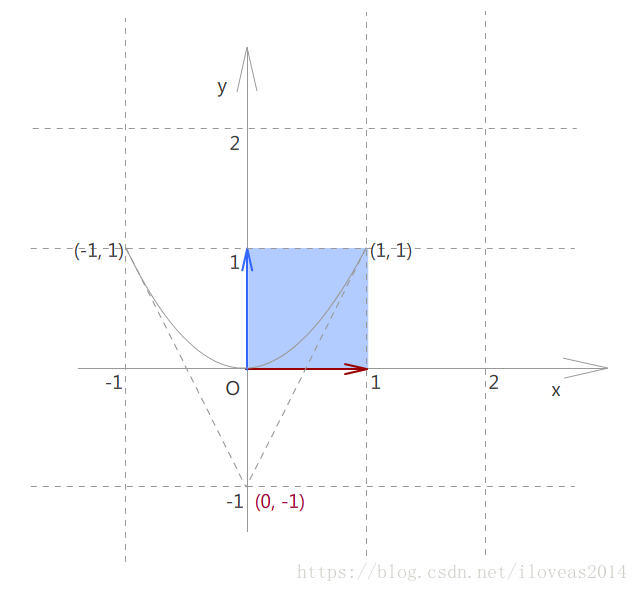
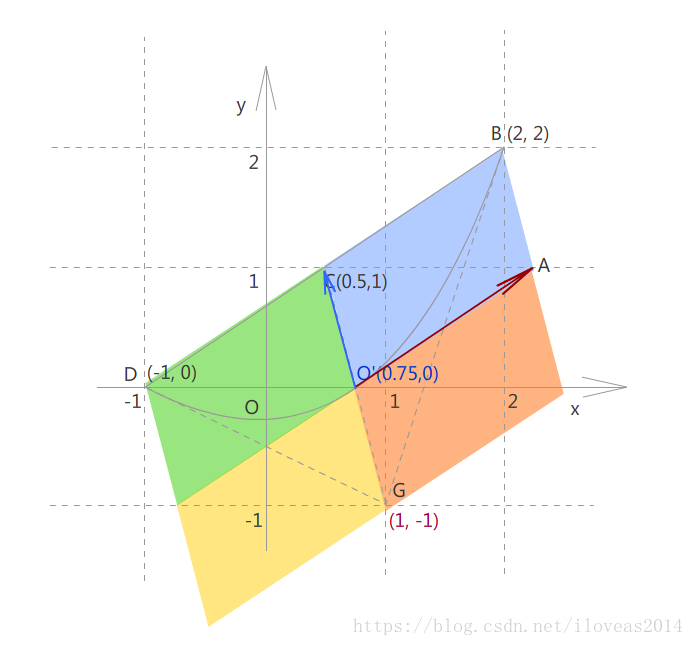
现在我们可以理直气壮地拿(0,0)到(1,1)这一个正方形来构建基向量。现在这是标准方程,基向量自然直接跟着坐标轴来,因此x方向的基向量为(1,0),y方向的基向量为(0,1)。
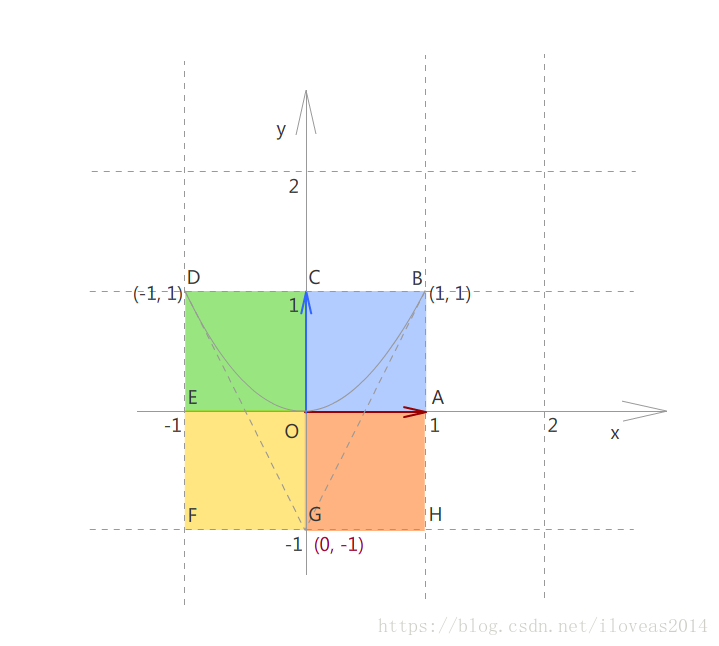
为了便于跟转换后的图形对照,我们把曲线以及端点和控制点连线所经过的所有网格也填上颜色,同时用字母标记上一些关键点。
A-H这8个点的坐标,现在我们一眼都能看出来,但映射到一般的贝塞尔曲线之后呢?还能直接看得出来么?反正我是看不出了。因此这里需要有一些特征性的东西来帮助我们在转换之后仍然不会迷失方向。
O是抛物线顶点,但跟贝塞尔曲线很难匹配到这个顶点。
A和E缺乏典型的几何特征,最多有OA和OE都跟抛物线相切,但O点都很难明确了,因此先放一放。
B和D分别是曲线的两个端点。
C是B和D连线的中点。
F和H的几何特征也不明显。
G是控制点坐标。
这里直接给出一个结论:矩阵变换为仿射变换,平行线在变形前后仍为平行线,若两平行线段(同一直线上的也算)长度相等,则变换后它们的长度也依然相等。证明从略。
由于BCD几何特征明显,所以,我们可以再加入AE平行于BD,FH平行于BD这两条线索。
另外还有两点:
1 OA为x方向的基向量,OC为y方向的基向量。
2 O是CG和抛物线和交点,也是抛物线的顶点。
下面我们尝试做个变换吧。比如下图这个样子。
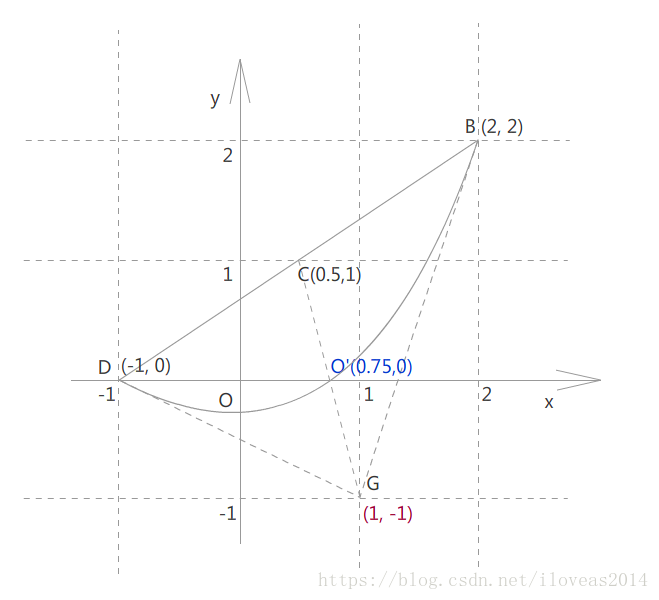
B,D,G直接是已知点,可以先画出来。接着C是BD连线的中点,也可以直接画得到。
然后,CG和贝塞尔曲线的交点对应的就是O点了,也刚好对应标准抛物线的顶点。
本来二次贝塞尔曲线和直线求交是要解二元二次方程组,但根据已有线索以及前面提到的矩阵变换的性质,O点刚好是CG的中点,因此能直接算出来是(0.75,0),已用蓝字表示。
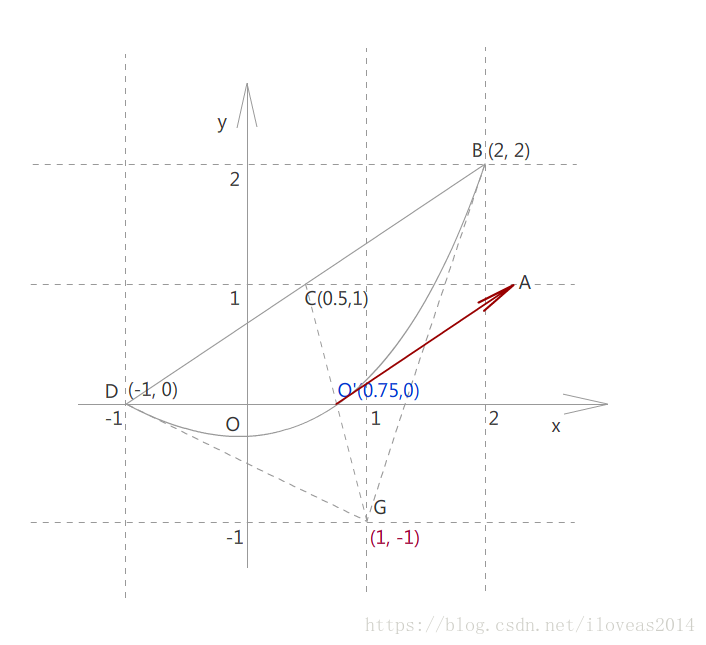
然后我们还知道,OA是x方向的基向量,它平行于CB并且长度跟CB相等。
因为我们的目标是求出基向量,所以A点坐标可以不算出来,然后向量OA=向量BC。
所以向量OA=B-C=(2,2)-(0.5,1)=(1.5, 1)
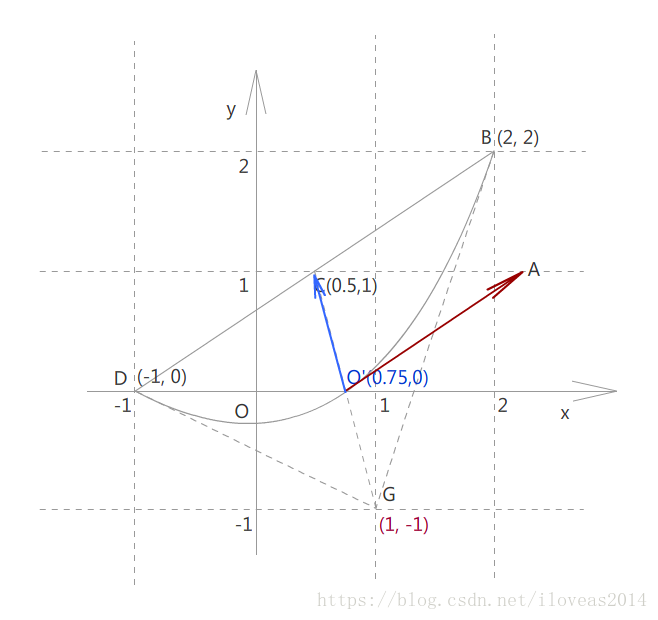
而向量OC直接等于y方向的基向量C-O'=(0.5, 1)-(0.75, 0) = (-0.25, 1)
PS:也可以不求O'点,直接取CG的一半
基向量求好了,但是可能有的朋友看着会懵逼,那我现在把色块也加上,并且把变换前的图像搬出来,给大家一个直观的形象。
跟砖块铺贴不一样,坐标原点上的抛物线顶点也跟着移动了。所以从标准方程到贝塞尔曲线方程,这里要分两步变换。
第一步是执行基向量矩阵变换,第二步是偏移(0.75, 0)。
在一周前(终于不是七八个月了)的连载十二中,我给出了基向量矩阵的推导过程,但这次我不用再不厌其烦地把那些让别人看着头痛的公式给搬过来再讲解一遍,因为在紧接着的连载十三中我给出了代码,然后我也不手算了,直接交由浏览器来算。
PS:跟前面变换二元二次方程不同,这里的变换不包含任何诸如xy这样的未知数,所以完全可以让任何非数学编程的高级语言来实现。所谓非数学编程语言,简单点理解就是我想实现传入一个表达式,然后无法直接生成计算后的表达式。比如
function sqr(n){
return n*n;
}
我们没有直接的方法让这个函数在传入"n-2"的时候给我返回"n^2-4n+4"
但是矩阵不存在这个问题,我们现在把代码搬过来就可以了。
var matrix = new Matrix();
var baseX = new Point(1.5, 1); //ex基向量
var baseY = new Point(-0.25, 1); //ey基向量
matrix.a = baseX.x;
matrix.b = baseY.x;
matrix.c = baseX.y;
matrix.d = baseY.y;
MatrixUtil.translate(matrix, 0.75, 0);
console.log(matrix.a, matrix.b, matrix.c, matrix.d, matrix.tx, matrix.ty);将输出如下结果(其实这么简单的,肉眼也能看得出来):
1.5 1 -0.25 1 0.75 0
我们先把曲线的点代入下,这条曲线的3个点分别为(-1,0),(1,-1)和(2, 2),故方程为:
接着我们知道旋转的套路是这样写的:
然后矩阵乘法的套路是这样写的:
按旋转的格式来就是这样:
于是我们代入到参数方程中,得到
然后矩阵的6个系数,前面输出过了,我们代进去:
然后解一下关于X,Y的二元一次方程组(怎么不用逆矩阵?因为t是未知数,不好通过代码实现,手算的话就无所谓了):
下式-上式,得到:
求X也用类似的方法:
然后发现
卧槽,还真的刚好是标准抛物线的方程诶!
至此,我们基本可以认为,这个基向量转换矩阵是正确的!有兴趣的童鞋可以自行把写死的数字换成字母再推导一次。
从标准抛物线到二次贝塞尔曲线,使用的是上述代码的矩阵,而如果要反过来,从二次贝塞尔曲线转换回标准的抛物线,那就是前面所提到的矩阵的逆矩阵了。
这里本来应该总结下的,但似乎已经写长了,放到下一篇吧,把图带着,然后逐个步骤写出来,相信大家还是能记得的,哈哈,下篇我用代码把转换矩阵实现出来,然后就可以尝试用它来进行一些简单的求交运算了,敬请期待!