复仇记第二篇,ICG博弈中的威佐夫博弈,它比巴什博弈更复杂,同样感谢博客https://blog.csdn.net/niushuai666/article/details/6638943
如果没有了解过巴什博弈的,建议先阅读上一篇巴什博弈:巴什博弈及证明
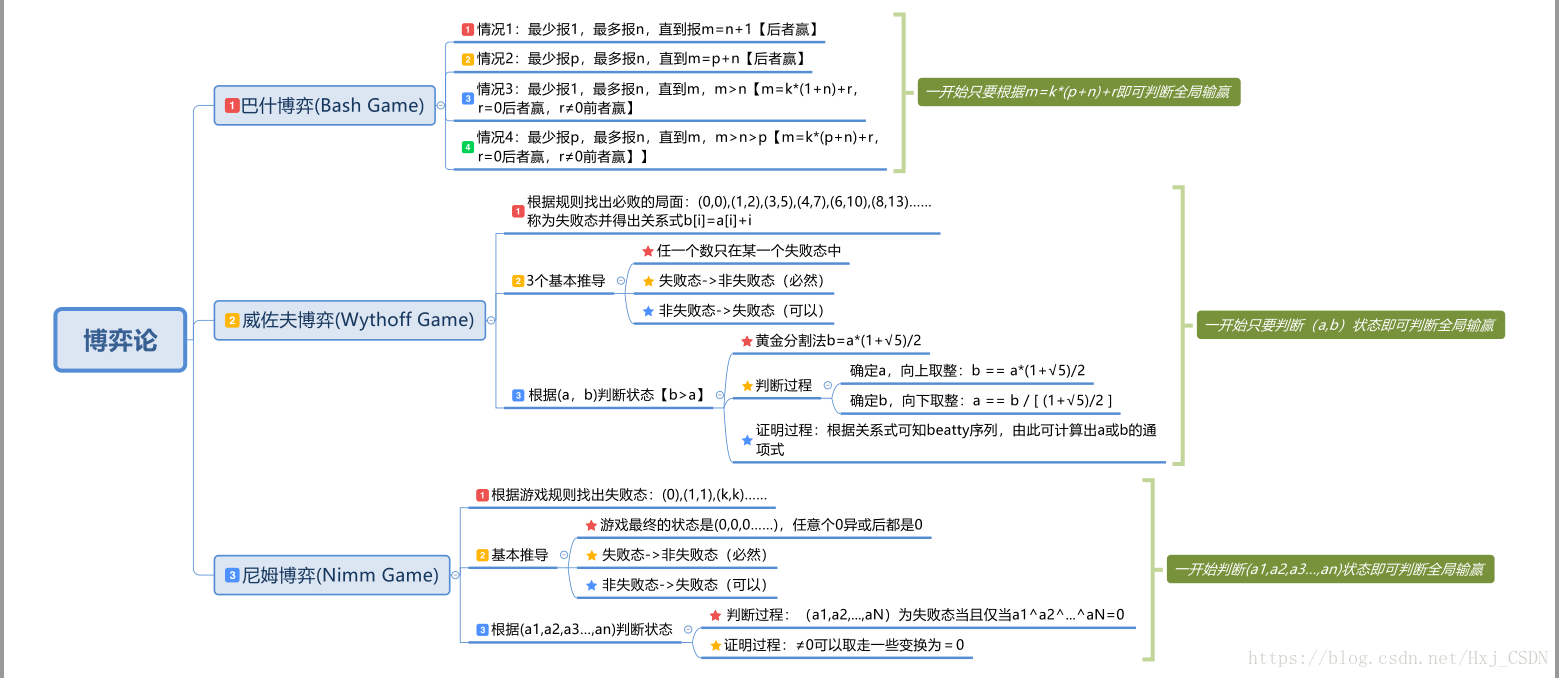
威佐夫博弈(Wythoff Game)
有两堆各若干个物品,两个人轮流从某一堆或同时从两堆中取同样多的物品,规定每次至少取一个,多者不限,最后取光者得胜。(假设A、B两人游戏,且A先行)
与巴什博弈思路一致,我们先找出必败态!(在此感叹号我们表示高兴,不表示阶乘)。找必败态的方法可以根据游戏规则一步步推算 或者 找出游戏规律,一大步一大步推算,由于后面证明的篇幅可能很长,所以找出必败态的过程在此不再说明,请阅读大神的文章:
大神链-SG函数
方法链-博弈论总结
现在我们约定用(x,y)代表两堆物品中剩下的数量状态,假设你已经知道如何找失败态了,而失败态是:(0,0),(1,2),(3,5),(4,7),(6,10),(8,13)……,为了猜想推算式,我们用 (an,bn)表示第n个失败态中两堆石子剩下an和bn,根据高中数学数列的思想,我们大胆假设,小心求证地猜想bn = an + n。
证明
观测到,由于an和bn都是递增的,要先证明这一点。
命题1: an+1=前n组必败态中未出现过的最小正整数
证明:根据SG函数可知,SG(x) = mex(S),其中 S 是 x 后继状态的SG函数值的集合,mex(S)表示最小的不属于这个集合的非负整数,因此an+1=前n组必败态中未出现过的最小正整数。
命题2: 如果(an,bn)为必败态,则bn = an + n
证明:使用归纳法,假设前k个必败态为(ak,ak+k),则第k+1个失败态为(ak+1,ak+1+k+1)。由SG性质可知,失败态的下一步一定为必胜态,而根据游戏规则,对于(ak+1,ak+1+k+1),我们有3种取法,分别是从左边拿走m、从右边拿走m和同时从两堆中拿走相同数量的m,只要证明这3种取法留下的局面都是必胜态即可。
①A从左边拿走m:此时留给B(ak+1 - m,ak+1+k+1)的局面。根据命题1我们知道,ak+1 > ak,bk+1 > bk,当从ak+1拿走m后,我们可以找到一个对应的p < k+1,使得ap ≤ ak+1 - m,同时bp = ap + p < (ak+1+k+1-m) < (ak+1+k+1),所以B只要确定ap后,再从右边的ak+1+k+1拿走一些成为bp (注意,拿走后bp不一定大于ap),必败态(ap,bp)【这里不分大小】又留给了A,所以从左边拿走m后的局面是必胜态。
②A从右边拿走m,此时留给B(ak+1,ak+1+k+1 - m)的局面。这里分3种情况,第1种是m比较小(m < k+1),保持着a < b,同理,拿走后有一个p < k+1 使得bp ≤ bk+1 - m,也有一个ap = bp - p < (ak+1+k+1 - m) < ak+1,因此(ak+1,ak+1+k+1 - m)可以从某一边或者同时两边取走一些,变成(ap ,bp)必败态留给A。第2种是m=k+1,此时留给B的局面是(ak+1,ak+1),B只需要同时取走ak+1留下(0,0)必败态给A即可。第3种是m比较大(m>k+1),取走后bk+1 < ak+1,此时调换一下位置变成(bk+1,ak+1)再使用①即可,必败态又留给A。
③同时从两堆中拿走相同数量的m,此时留给B(ak+1 - m,ak+1+k+1 - m)的局面,根据①可知, 存在ap ≤ ak+1 - m ,bp < (ak+1+k+1-m) ,所以B可以从某一边或者同时从两边取走一些把(ak+1 - m,ak+1+k+1 - m)变成(ap,bp)的必败态留给A。
综上所述,对于(ak+1,ak+1+k+1)无论怎么走,下一步都是必胜态,因此(ak+1,ak+1+k+1)为必败态,所以 bn = an + n成立。这个证明确实比较复杂,需要慢慢细细地思考。
归根到底,bn = an + n只是一个递推式,要从根点(0,0)开始才能获得某个失败态,比如给你一个局面(101,234),你无法判断局面输赢,虽然你可以得到234=101+133,但是不能判断a[133]是否等于101我们是不知道的,因此我们需要找出a[n]或者b[n]的通项公式,就可以随便根据一个局面(x,y)去判断全局输赢了。
要找出an或者bn的通项公式,涉及到Beatty序列,Beatty序列在此不再详细介绍,简单而言,由α、β两个无理数构成1/α + 1/β = 1,取n为任意正整数且an= ⌊α*n⌋,bn= ⌊β*n⌋(⌊x⌋代表向下取整),序列an和bn就称为Beatty序列,和Beatty定理对比,发现我们的an和bn完全符合Beatty序列的性质,所以可以从Beatty定理中计算出α、β,从而得到an或者bn的通项公式,计算过程如下:
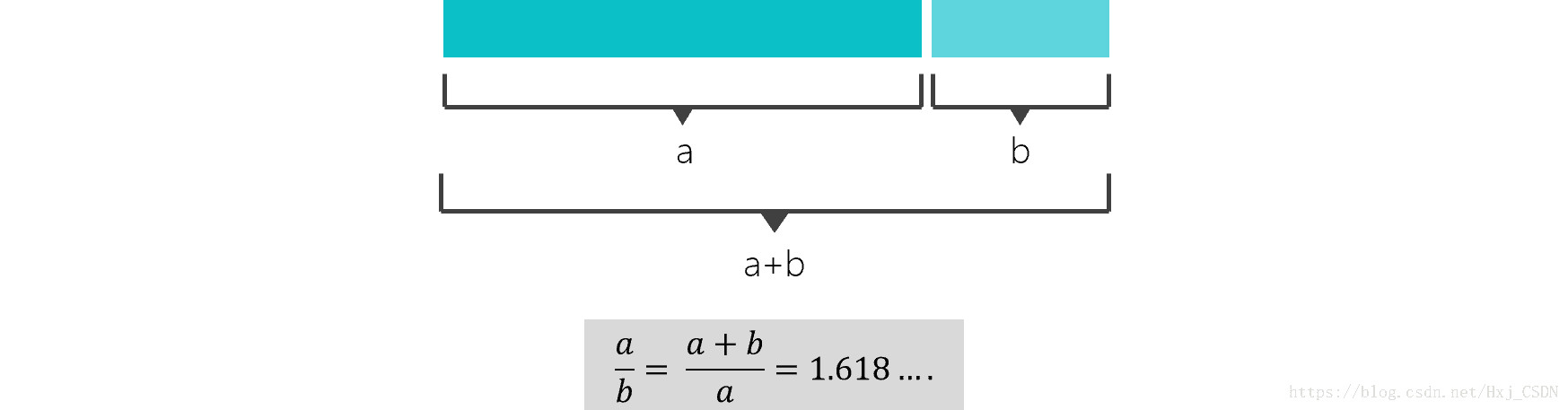
已知Beatty序列:an= ⌊α*n⌋,bn= ⌊β*n⌋,而bn = an + n = ⌊α*n⌋ + n = ⌊(α+1)*n⌋,于是β = (α+1),代入1/α + 1/β = 1,解得α =(1+√5)/ 2 ≈ 1.618,这个数字就是黄金比例数!!
宿命论说:一切冥冥之中自有安排(虽然比较消愁,不过用在这里很合适),自然界中的事物确实有着某种人类未知的联系,这种联系是宇宙大爆炸后就存在的,人类不能创造,只能发现它,在威佐夫博弈中居然出现了一个与此毫不相关的黄金比例,真是令人惊讶,第一个计算出这个结果的人会不会刷新TA的世界观。
判断方法
因此,an的通项公式为:an = ⌊n *(1+√5)/ 2⌋,一般(1+√5)/ 2 ≈ 1.618,直接取1.618
所以,对于任一个局面(a,b),假设a<b,要判断是否为必败态的算法有多个,可以根据bn = an + n,也可以根据 bn \ an = 1.618,小白根据后者列出算法,有2种:
①确定a,于是要算出b‘与原来的b比较是否相等,由于 b’ / a = 1.618,因此 b‘ = a * 1.618,因为1.618是比(1+√5)/ 2小,结果会偏小,所以这里要向上取整,也就是b’ = ⌈ a*1.618 ⌉,如果 b==b’为真,则(a,b)为必败态,否则为必胜态。
②确定b,于是要算出a’与原来的a比较是否相等,因此a’ = b \ 1.618,因为1.618是比(1+√5)/ 2小,结果会偏大,所以这里要向下取整,也就是a’ = ⌊b \ 1.618⌋,如果a==a’为真,则(a,b)为必败态,否则为必胜态。
小白也许描述得不够清楚,因此各位有必要访问一下大牛:威佐夫博弈,Beatty定理和黄金分割数
此文为威佐夫博弈,还有最后一篇尼姆博弈。