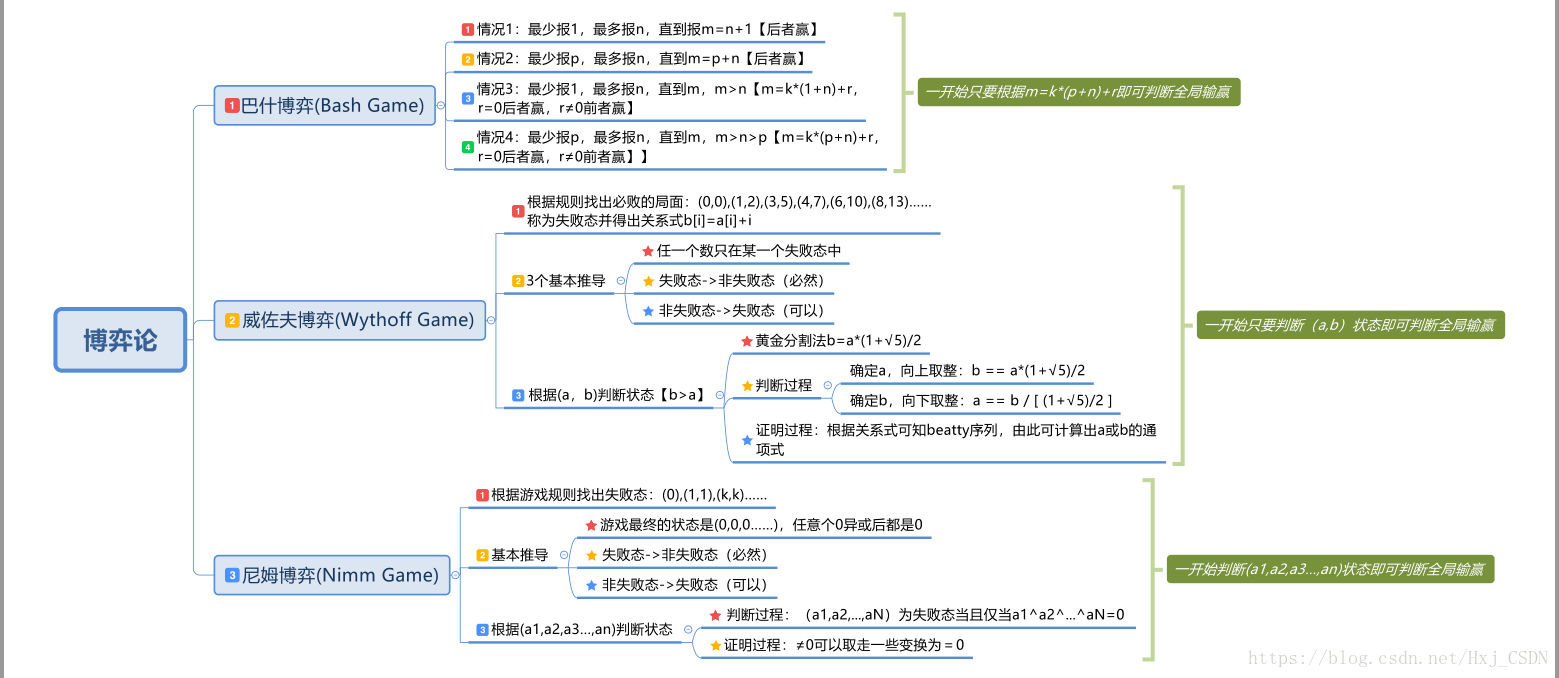
这是最后一篇ICG博弈,尼姆博弈,对比前面的巴什博弈和威佐夫博弈,尼姆博弈的玩法更加自由化,因此想赢的过程也更加复杂。
如果没有了解过巴什博弈和威佐夫博弈的,建议先看上两篇 :巴什博弈及证明 威佐夫博弈及证明
尼姆博弈(Nimm Game)
目前有任意堆石子,每堆石子个数也是任意的,双方轮流从中取出石子,规则如下:
①每一步应取走至少一枚石子;每一步只能从某一堆中取走部分或全部石子;
②如果谁取到最后一枚石子就胜。
设(a,b,c,d…)为每堆石子的个数(石子个数>=0),甲乙两人游戏,且甲先行。
一样的思路,找出必败态,这里用递增穷举的方法:
剩下1堆石子,明显(0)是一个必败态,(k)是一个必胜态。
剩下2堆石子,根据游戏规则可知,(1,1)是一个失败态,(1,2)是一个必胜态,(2,2)是一个失败态,……发现(k,k)是一个必败态,无论你怎么取,对手只要从数量较多的一堆取走和你取走一样的数量,则又回到了(k‘,k’)状态,这样一直下去,总会变成(1,1)直到(0,0),(k,k+m)是一个必胜态。
剩下3堆石子,根据前面的结论,我们知道 (1,1,k)、(1,k,k)和(k,k,k)都是必胜态【都可以留下(k,k)必败态给对手】,接下来对于任一个(a,b,c)都可以转化为(k+m,k+n.k+p),而对于m\n\p,有3种情况,分别是①三者相等,就是(k’,k’,k’),为必胜态。②两者相等,假设为(k+m,k+p.k+p),这样把k+m取完,留下必败态给对手,也是必胜态。③三者不等,这种情况非常复杂,用简单的公式难以表达,我们可以观察到(1,2,3)是必败态,但是(1,2,4)是必胜态,两者只是相差一个石子,因此这里先搁一搁。
……
经过一些简单的穷举,尽管难以发现递归式或者通项公式,但是我们还是能感觉到一点非常重要的因素:一个状态是必胜态还是必败态,与剩下的石子堆之间是否相等有很大的关系。上面3种穷举的结果如下:
必败态:(0)、(k,k)
必胜态:(k)、(k,k+m)、(k,k,k)、(m,k,k)
小白猜想不了这种规律的表达,但是被别人与计算机二进制的异或运算联系了起来(这个人是谁,小白也不知道),对于异或运算⊕,也是和运算对象是否相等有关,小白的记忆方法是 异1同0,也就是对于二进制:
| A | B | A⊕B |
|---|---|---|
| 0 | 0 | 0⊕0 = 0 (同0) |
| 0 | 1 | 0⊕1 = 1 (异1) |
| 1 | 0 | 1⊕0 = 1 (异1) |
| 1 | 1 | 1⊕1 = 0 (同0) |
两个相异的数异或⊕就是1,两个相同的数异或⊕就是0。
使用异或运算,可以根据当前局面判断全局输赢,判断过程是:对于当前局面(a1,a2,a3……an),如果a1⊕a2⊕a3⊕……⊕an = 0,那么当前局面就是必败态,否则是必胜态。
我们先代入穷举出来的结果:
(0)、(k,k):异1同0,确实k⊕k = 0,为必败态。
(k)、(k,k+m)、(k,k,k)、(m,k,k):异1同0,确实k⊕(k+m) ≠ 0,k⊕k⊕k ≠ 0,m⊕k⊕k ≠ 0,为必胜态
证明
命题:尼姆博弈,如果当前局面(a1,a2……an)中,a1⊕a2⊕……⊕an = 0,那么当前局面是必败态。
证明:明显当a1=a2=……=an = 0的时候成立,(0)为必败态。当(a1,a2……an)不全等于0的时候,有2种情况:
① k = a1⊕a2⊕…⊕am⊕…⊕an ≠ 0,此时k的二进制最高位为1,则一定存在am它的最高位也为1,因为异或运算保证了当运算结果为1的时候,某一方一定是1,于是ap = am ⊕ k < am【异1同0,两个最高位的1异或得到0】,此时把am替换为ap,(a1⊕a2⊕…⊕ am ⊕…⊕an) => (a1⊕a2⊕…⊕ ap ⊕…⊕an) = (a1⊕a2⊕…⊕ am ⊕ k ⊕…⊕an)=(a1⊕a2⊕…⊕ am ⊕…⊕an⊕ k) = k ⊕ k = 0,这个过程证明了 当 a1⊕a2⊕……⊕an ≠ 0的时候,存在有效的取法ap = am ⊕ k使得取后的 结果a1⊕a2⊕……⊕an = 0。
② k = a1⊕a2⊕…⊕am⊕…⊕an = 0,根据游戏规则,必须从am中至少取走1个成为ap < am,可以用反证法得到a1⊕a2⊕…⊕ap⊕…⊕an ≠ 0,假设a1⊕a2⊕…⊕ap⊕…⊕an = 0,那么(a1⊕a2⊕…⊕am⊕…⊕an) = (a1⊕a2⊕…⊕ap⊕…⊕an) = 0,两边依次同时异或aj(j从1递增到n,j ≠m,p),就可以得到ap = am,与前提ap < am矛盾,假设不成立,这个过程证明了 当a1⊕a2⊕…⊕am⊕…⊕an = 0的时候,不存在有效的取法让取后的结果a1⊕a2⊕…⊕am⊕…⊕an = 0。
综上所述,当a1⊕a2⊕……⊕an ≠ 0的时候,存在有效的取法,令到a1⊕a2⊕……⊕an = 0,而a1⊕a2⊕……⊕an = 0不存在有效的取法使得a1⊕a2⊕……⊕an = 0【也就必胜态有办法让下一步为必败态,必败态下一步一定为必胜态】,随着局面的变化,a1⊕a2⊕……⊕an = 0最终会变成(0,0,0……0)也就是(0)必败态,所以如果当前局面(a1,a2……an)中,a1⊕a2⊕……⊕an = 0,那么当前局面是必败态。
如果不够明白,可以访问 大神链
这是最后一篇,尼姆博弈