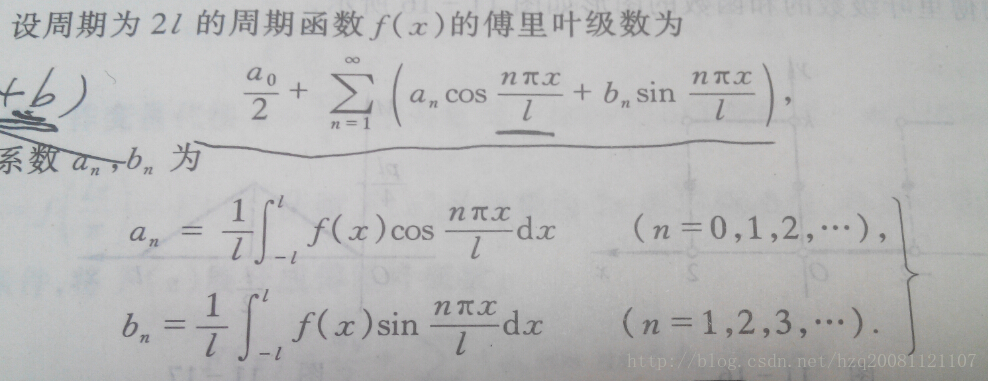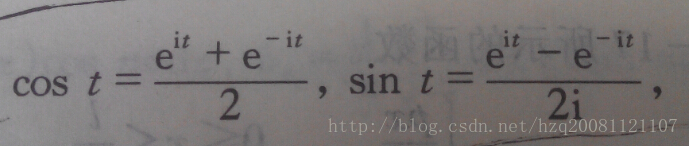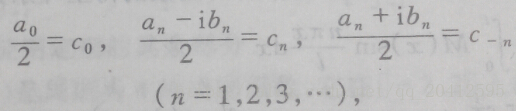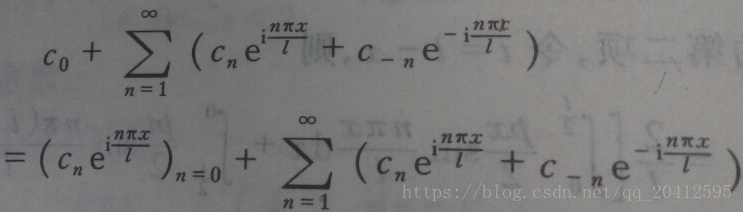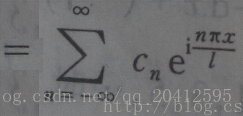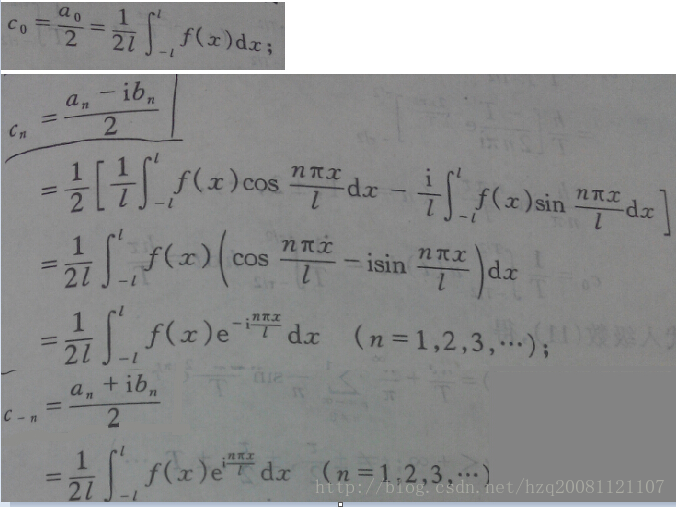目录
这里分享下麻省理工大学的 傅里叶的公开视频课:http://open.163.com/movie/2006/1/9/H/M6TUO44DQ_M6TUPN09H.html
有助理解傅里叶变换的几个图:
三角函数的叠加,如何得到方波:
(时域上观察)
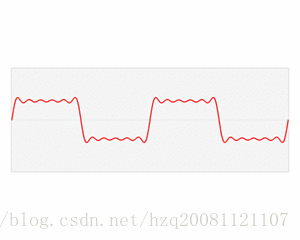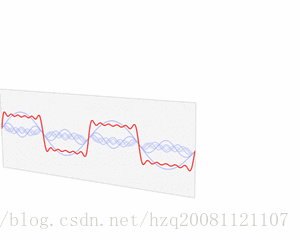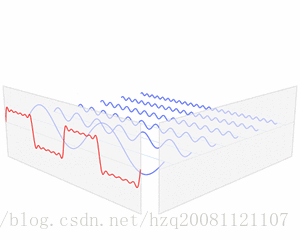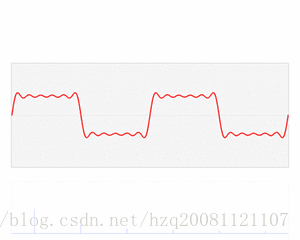
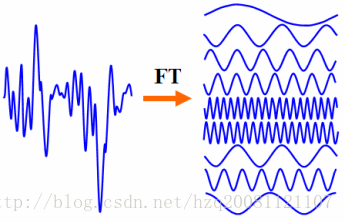
时域特征转换到频域特征:
杂乱的周期波形信号(如语音)可以转换为规则的三角波型号的叠加:
1.傅里叶级数
2.傅里叶变化
更多详细的内容请看:https://zhuanlan.zhihu.com/p/19763358?columnSlug=wille
傅里叶级数的本质是将一个周期的信号分解成无限多分开的(离散的)正弦波,但是宇宙似乎并不是周期的。
是否有一种数学工具将连续非周期信号变换为周期离散信号呢?抱歉,真没有。
比如傅里叶级数,在时域是一个周期且连续的函数,而在频域是一个非周期离散的函数。这句话比较绕嘴,实在看着费事可以干脆回忆第一章的图片。
而在我们接下去要讲的傅里叶变换,则是将一个时域非周期的连续信号,转换为一个在频域非周期的连续信号。
算了,还是上一张图方便大家理解吧:
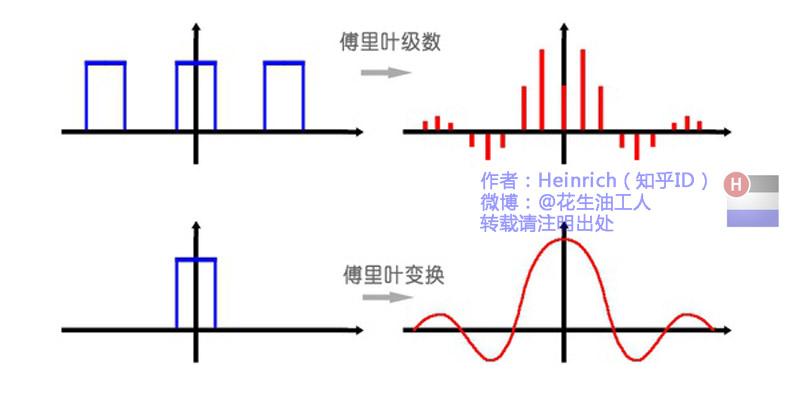
或者我们也可以换一个角度理解:傅里叶变换实际上是对一个周期无限大的函数进行傅里叶变换。
3.指数形式的傅里叶变换
欧拉公式:
虚数i这个概念大家在高中就接触过,但那时我们只知道它是-1的平方根,可是它真正的意义是什么呢?
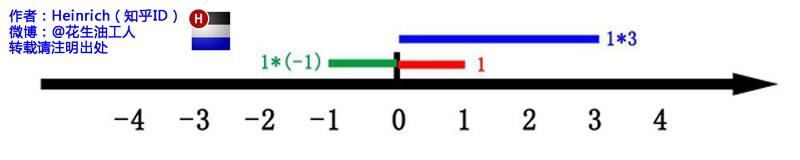
这里有一条数轴,在数轴上有一个红色的线段,它的长度是1。当它乘以3的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以-1的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了180度。
我们知道乘-1其实就是乘了两次 i使线段旋转了180度,那么乘一次 i 呢——答案很简单——旋转了90度。
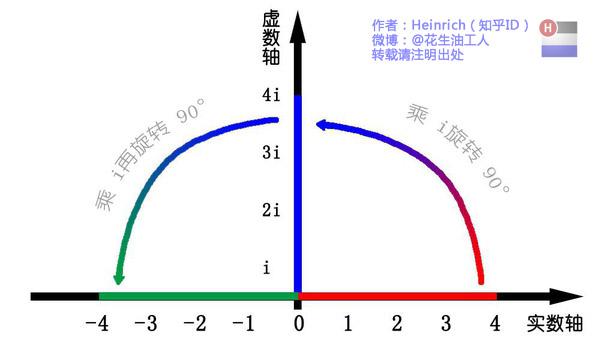
同时,我们获得了一个垂直的虚数轴。实数轴与虚数轴共同构成了一个复数的平面,也称复平面。这样我们就了解到,乘虚数i的一个功能——旋转。
现在,就有请宇宙第一耍帅公式欧拉公式隆重登场——
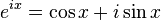
这个公式在数学领域的意义要远大于傅里叶分析,但是乘它为宇宙第一耍帅公式是因为它的特殊形式——当x等于Pi的时候。
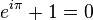
这个公式关键的作用,是将正弦波统一成了简单的指数形式。我们来看看图像上的涵义:
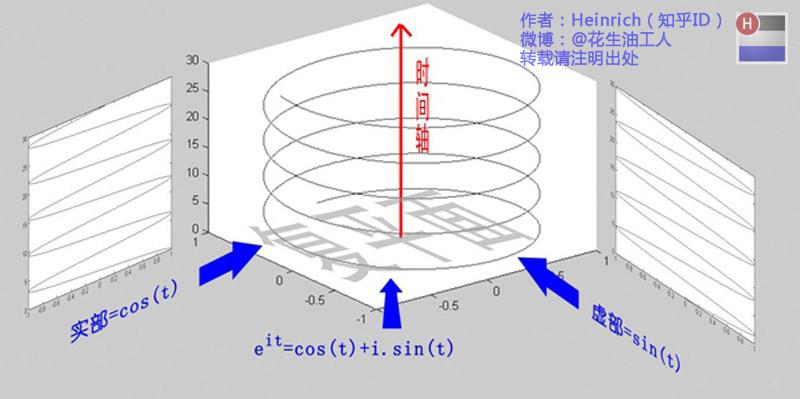
欧拉公式所描绘的,是一个随着时间变化,在复平面上做圆周运动的点,随着时间的改变,在时间轴上就成了一条螺旋线。如果只看它的实数部分,也就是螺旋线在左侧的投影,就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。
4.复数形式的傅里叶级数
另一种需要借助欧拉公式的另一种形式去理解:
将以上两式相加再除2,得到:
这个式子可以怎么理解呢?
我们刚才讲过,e^(it)可以理解为一条逆时针旋转的螺旋线,那么e^(-it)则可以理解为一条顺时针旋转的螺旋线。而cos(t)则是这两条旋转方向不同的螺旋线叠加的一半,因为这两条螺旋线的虚数部分相互抵消掉了!
举个例子的话,就是极化方向不同的两束光波,磁场抵消,电场加倍。
这里,逆时针旋转的我们称为正频率,而顺时针旋转的我们称为负频率(注意不是复频率)。
通过欧拉公式可以将三角函数形式的傅里叶变换转为复数形式:
上图的公式看起来不简洁,我们借助一些符号代换让上式看起来简单一些:
Cn的求解,我们已经知道an、bn的求解方法为在对应周期上做积分,Cn和an、bn的关系的关系展开可以得到:
参考资料:傅里叶分析 https://zhuanlan.zhihu.com/p/19763358?columnSlug=wille