文章目录

前言
四、曲线(Curves)
五、曲面(Surfaces)
课程的最后

前言

曲线和曲面

四、曲线(Curves)

运用曲线，我们可以制作摄像机路径，动画曲线，向量字体等等。

贝塞尔曲线(Bezier Curves)

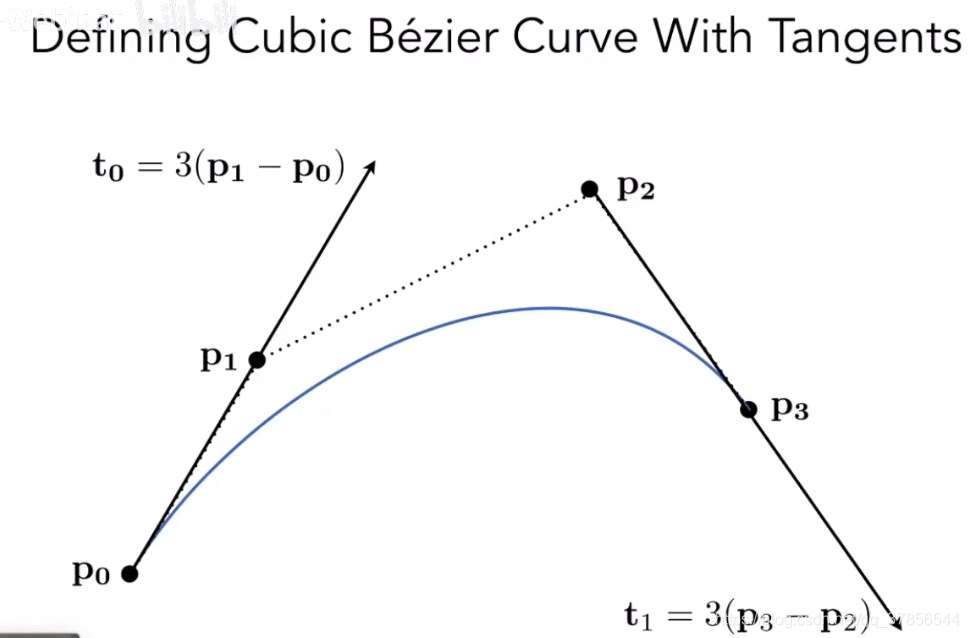
在这里插入图片描述
如上图，通过这四个点，我们能确定一条通过p0，p3，并且起始切线为p1-p0，离开的切线为p3-p2的曲线。

贝塞尔曲线的德卡斯特里奥算法(Bezier Curves - de Casteljau Algorithm)

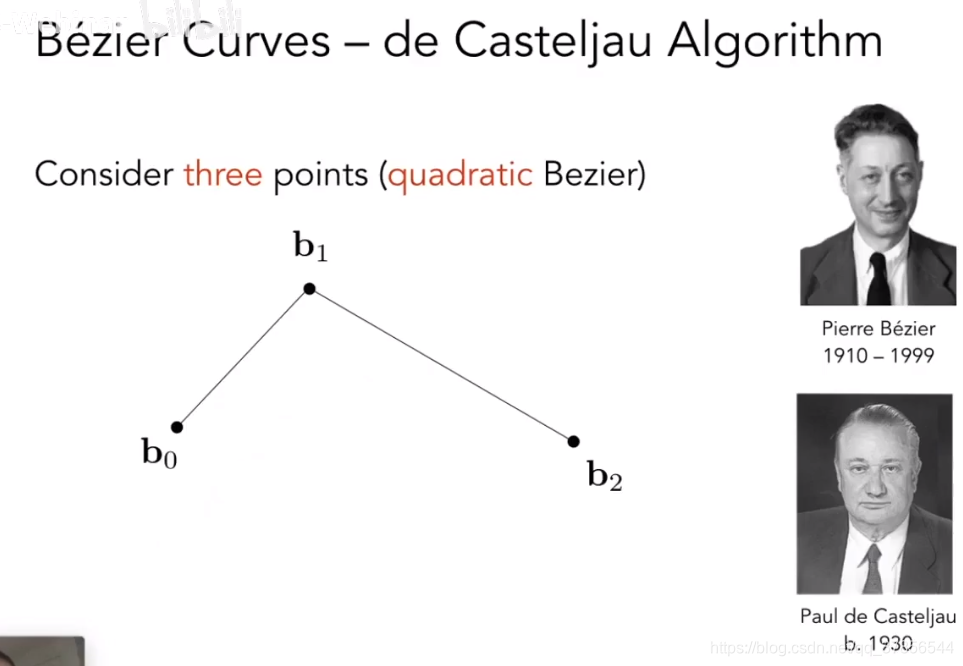
在这里插入图片描述
假设这里有三个点。要通过这三个点画贝塞尔曲线，其实任务就是找到曲线上的点在哪里。这里三个点生成的贝塞尔曲线叫做二次贝塞尔曲线(Quadratic Bezier)。

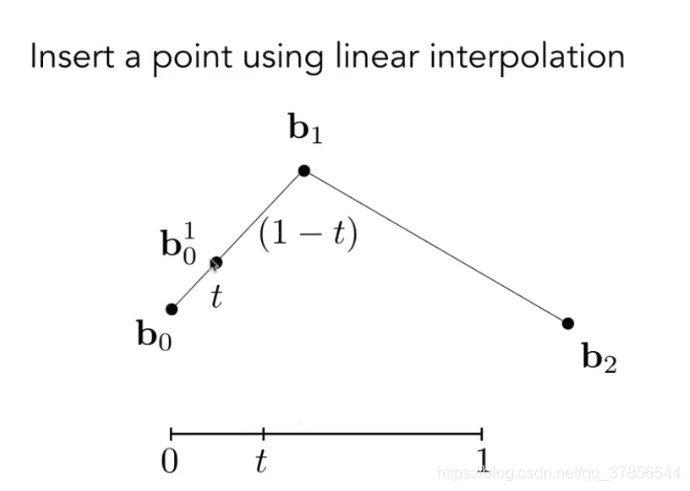
用线性插值在b0b1上插入任意点t，范围[0, 1]

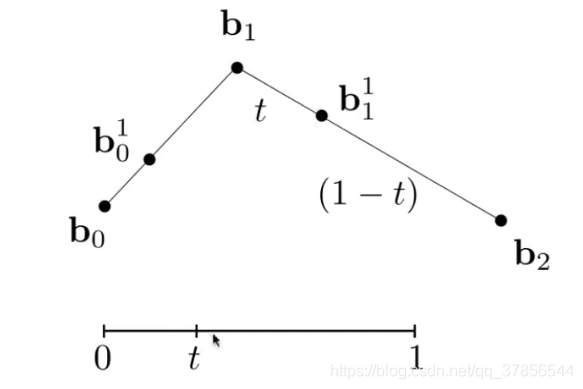
同样的，按相同比例在b1b2上也插入对应的t点。
在这里插入图片描述
我们将找到的两个t点连起来，再在得到的线段上按相同比例插入t点。找到的这个t点就是要算的贝塞尔曲线在t（可以理解为时间）时的点。

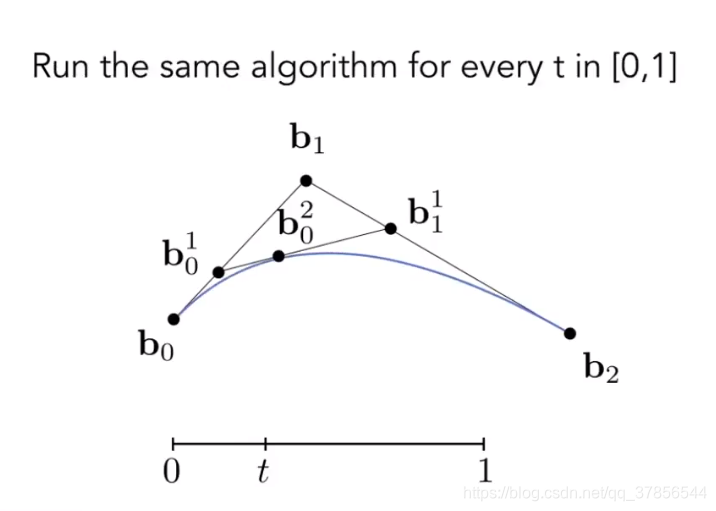
接下来，找到线段范围[0, 1]中的所有点t。贝塞尔曲线就得到了。
贝塞尔曲线是显式几何表示，因为有参数t。

三次贝塞尔曲线(Cubic Bezier Curve - de Casteljau)

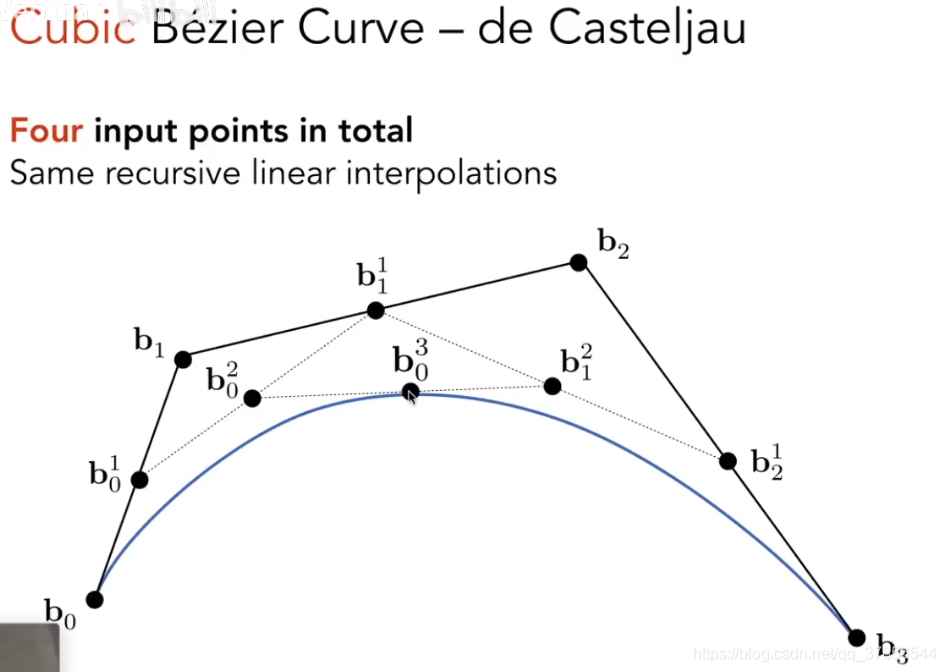
在这里插入图片描述
三次和二次一样，做同样的递归线性插值。

贝塞尔曲线的代数公式(Bezier Curve - Algebraic Formula)

在这里插入图片描述
de Casteljau算法给出了一个金字塔系数(pyramid of coefficients)。

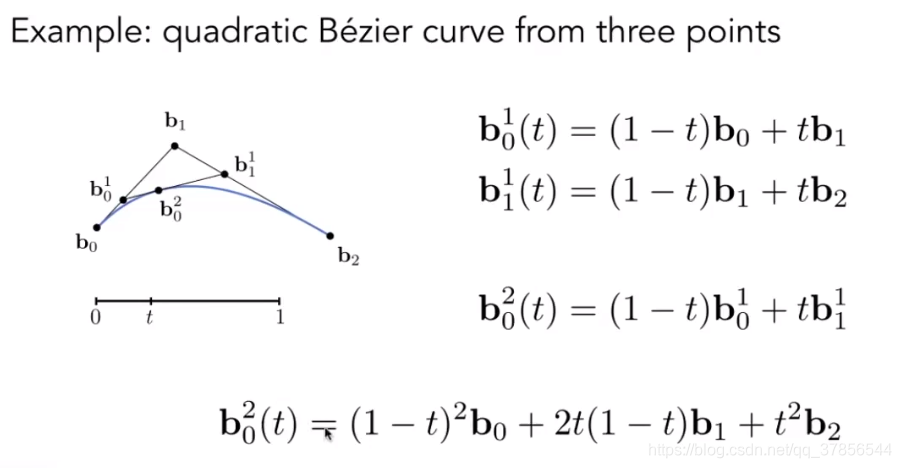
以二次贝塞尔曲线为例，公式如上图。如果是三次贝塞尔曲线，我们大可继续推下去。

上图为n阶贝塞尔曲线的伯恩斯坦形式。是上述代数式的总结。
在这里插入图片描述
伯恩斯坦形式的运用实例。假设有4个点，多项式定义了这4个已知点和t与贝塞尔曲线上的点的对应关系。

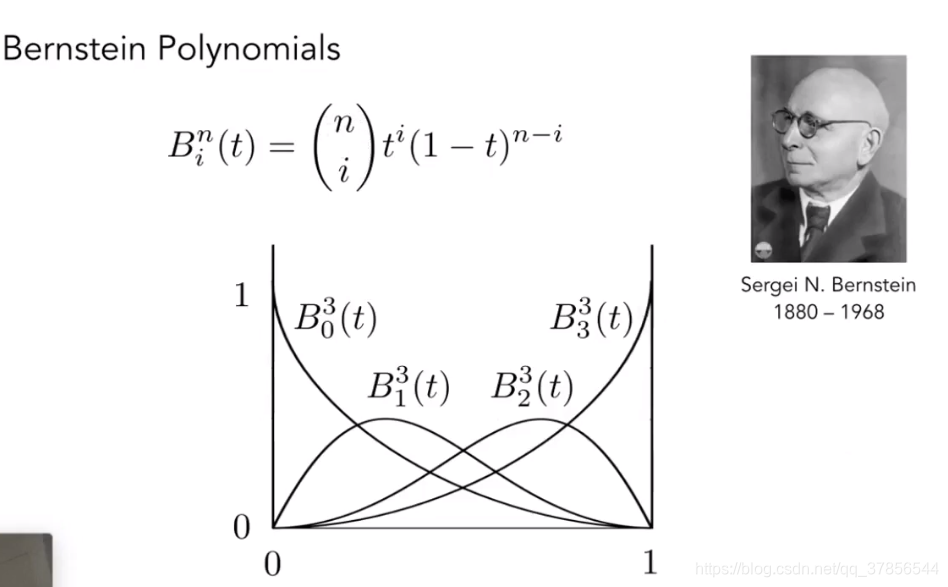
上图为伯恩斯坦多项式。

贝塞尔曲线的性质(Properties of Bezier Curves)

在这里插入图片描述
贝塞尔曲线在起点和重点一定在两个控制点上。也就是t = 0时在起点，t = 1时在终点。
贝塞尔曲线的起始点切线方向一定是b1 - b2，终点切线方向一定是b3 - b2。
在仿射变换下，变换控制点在重新得到的贝塞尔曲线和将贝塞尔曲线直接进行变换得到的结果是一样的。这样我们可以只变换控制点。
贝塞尔曲线一定在控制点形成的凸包(Convex hull)内，这叫做凸包性质。

什么是凸包(Convex Hull)

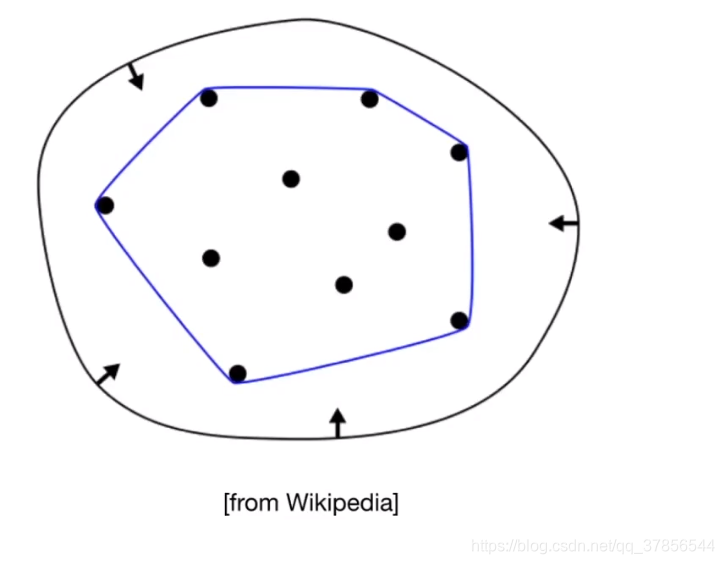
在这里插入图片描述
凸包是能够包围给定的一系列几何形体的最小凸多边形。凸多边形（Convex Polygon）指如果把一个多边形的所有边中，任意一条边向两方无限延长成为一直线时，其他各边都在此直线的同旁，那么这个多边形就叫做凸多边形。
可以想象上图中的合适圆点是钉子，你拿一根橡皮筋把这些钉子包住，橡皮筋收缩形成的外框就是凸包。

分段贝塞尔曲线(Piecewise Bezier Curves)

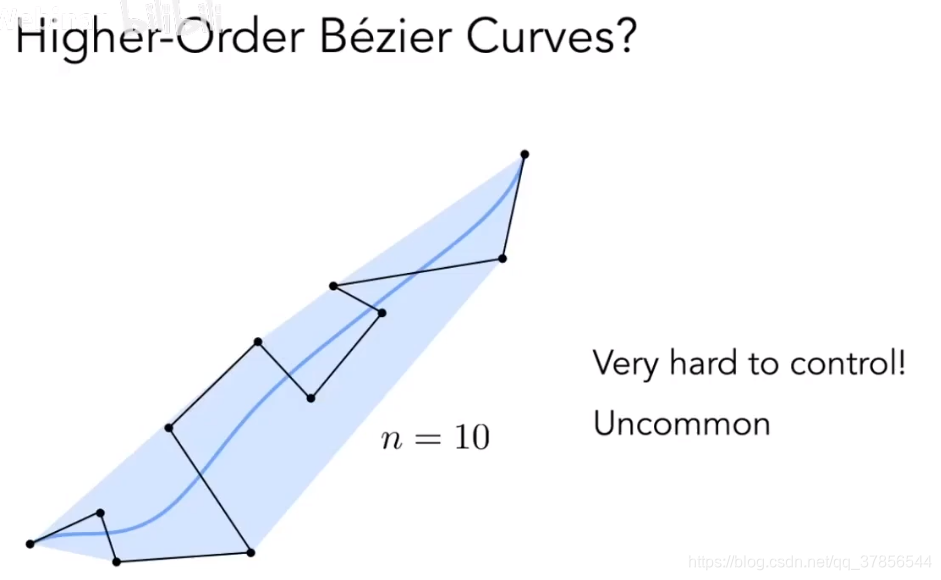
在这里插入图片描述
当遇到高阶贝塞尔曲线时，虽然我们依然可以算出曲线的样子，但是我们会发现很难再通过调整控制点来实现我们想要的形状。

那么我们可以通过，将高阶贝塞尔曲线拆成几个低阶贝塞尔曲线来进行单独调整，完成之后再将这几个低阶贝塞尔曲线连接成一条高阶贝塞尔曲线。这就叫分段贝塞尔曲线。特别的，人们通常将高阶贝塞尔转换为4个控制点的三次贝塞尔曲线。
思考一下Adobe PS/AI中的钢笔工具。

分段贝塞尔曲线的连续性(Continuity)

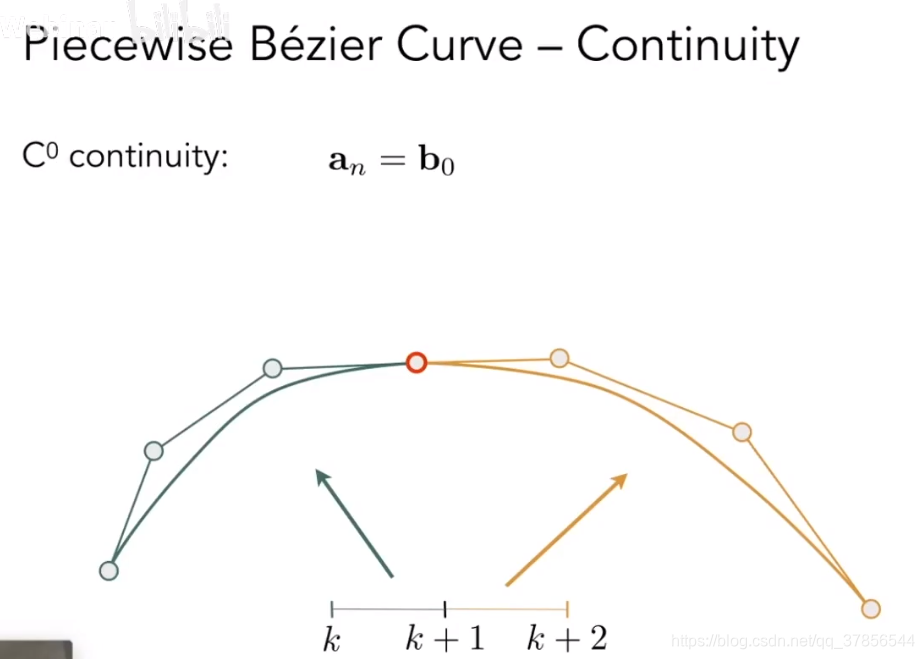
在这里插入图片描述
上图为C0连续，只要两条曲线在一个点连在一起就行。

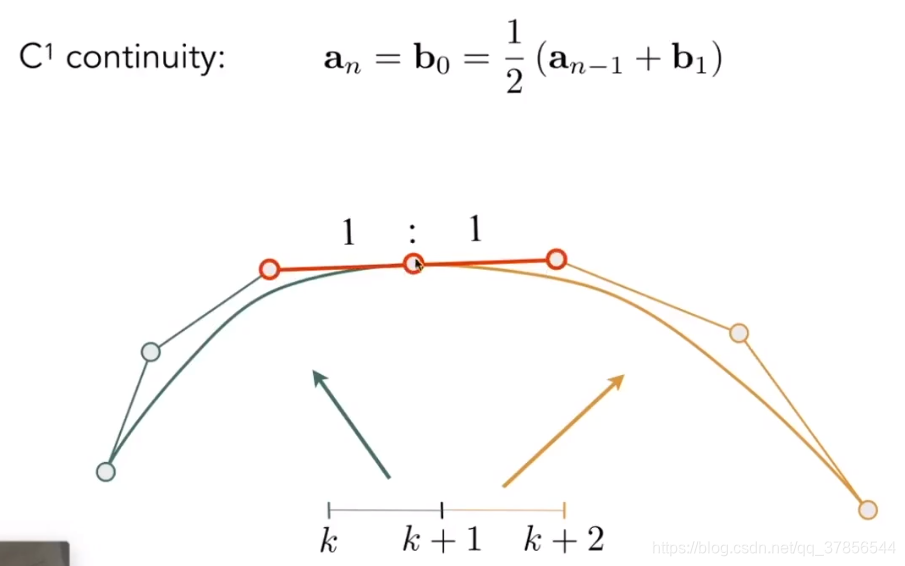
上图为C1连续，需要两天曲线终点和起点的切线共线，方向相反，同时要求连接点的左右相邻两点距离连接点的长度一样。高级一点的说法为，连接点的一阶导数连续。
除此之外，还可以有更高端的连续方式。比如C2要求二阶导数连续。

样条(Splines)

在这里插入图片描述
样条是穿过给定点集的方式构造的一条连续曲线，并且拥有一定数量的连续状态求导(Continuous Derivatives)。
简单来说，一个可控的曲线就是样条。

B样条(B - Splines)

B样条是基函数样条的缩写(Basis Splines)。函数空间中的每个连续函数可以表示为基函数的线性组合。
B样条是对贝塞尔曲线的一种拓展，满足贝塞尔曲线的全部重要特性，相较于贝塞尔曲线需要更多的信息。
B样条还满足局部性，能够不通过分段贝塞尔曲线实现局部调整。

五、曲面(Surfaces)

贝塞尔曲面(Bezier Surfaces)

在这里插入图片描述
将贝塞尔曲线拓展到面上。

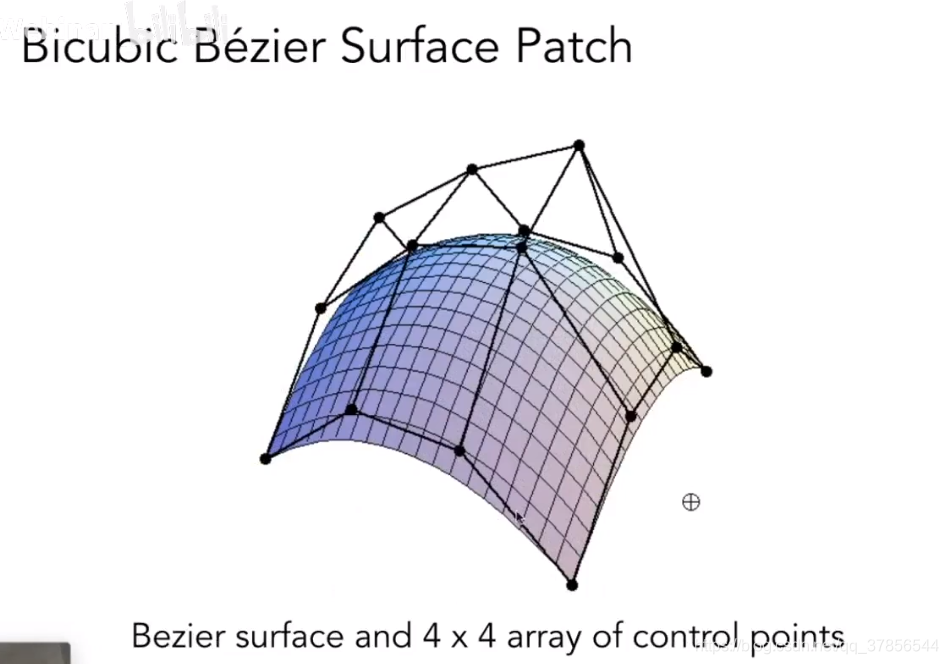
上图展示了通过4 X 4控制点定义的贝塞尔曲面。

贝塞尔曲面上的点的位置计算

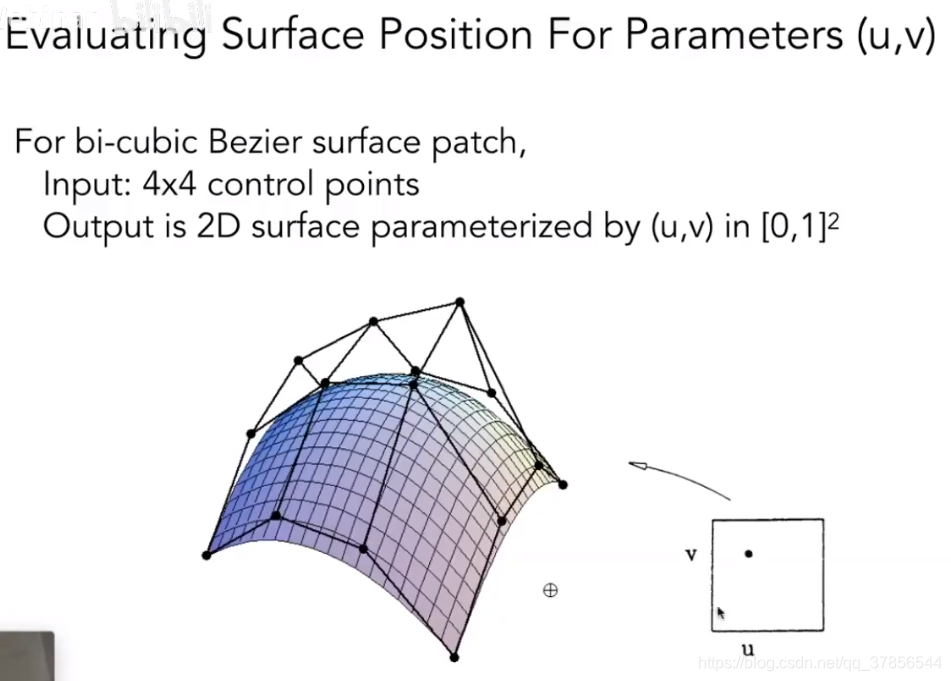
在这里插入图片描述
通过4 X 4控制点，得到一个参数化为(u, v)的范围为[0, 1]的二维平面，这个uv用来作为接下来的参数。

再通过之前的一维德卡斯特里奥算法(de Casteljau Algorithm)算出在四个贝塞尔曲线上的u点，再算出在四个贝塞尔曲线上的四个u点上的v点。就得到了曲面在参数(u, v)上的点的位置。
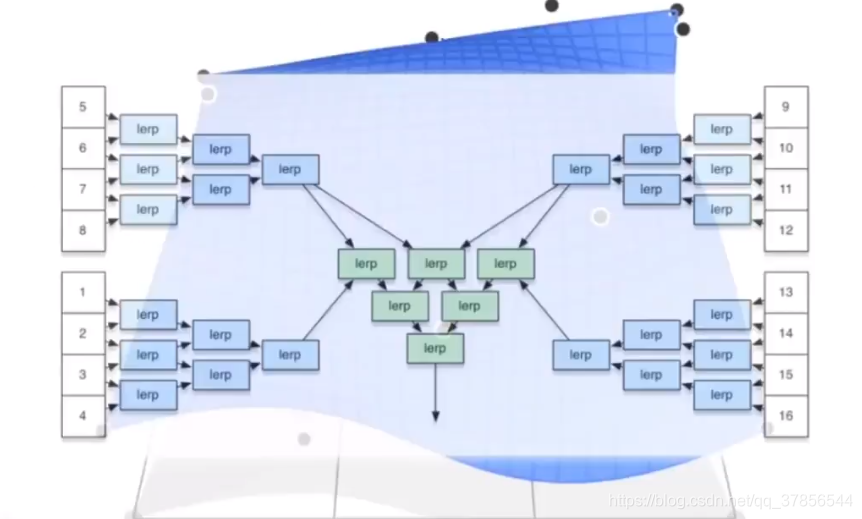
在这里插入图片描述
所以，贝塞尔曲面也是显式的几何，上图为具体算法的图示。

几何处理

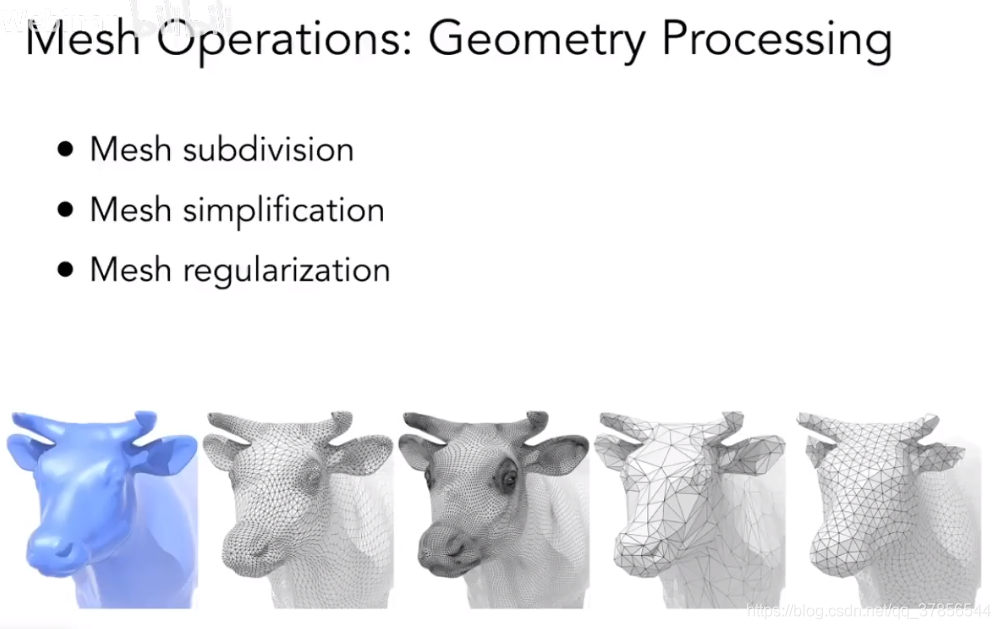
在这里插入图片描述
网格细分(Mesh Subdivision)如上图前三张图所示，用更多的三角形得到更光滑的表面。
网格简化(Mesh Simplification)，网格细分的逆过程。
网格规则化(Mesh Regularization)，将模型中的三角形都转变为更接近正三角形的形式。

课程的最后

B样条极其复杂，在本次课程中不涉及细节。同样不涉及的还有更复杂的非均匀有理B样条(Non-Uniform Rational B-Splines, NURBS)。
本次课程同样不涉及曲线操作的细节。
详细知识可前往清华大学-计算机图形学基础（国家级精品课）

几何Geometry(2)(曲线和曲面)（笔记）