一、相切模型
分析:设函数\(y=kx\)与函数\(y=lnx\)切点为\(Q(x_0,y_0)\),则有
\(\begin{cases} y_0=kx_0 \\ y_0=lnx_0 \\ k=f'(x_0)=\cfrac{1}{x_0}\end{cases}\);
从而解得\(x_0=e,y_0=1,k=\cfrac{1}{e}\),故切点\(Q\)的坐标为\((e,1)\)
二、直线和曲线相切
【分析】将原本数的问题,转化为形的问题,即两个函数的图像有交点的问题,从形上来处理解决。
【解答】由题目可知,方程\(\sqrt{3-\frac{3}{4}x^2}=x+m\)有实根,
即函数\(y=f(x)=\sqrt{3-\frac{3}{4}x^2}\)和函数\(y=x+m\)的图像有交点,
其中函数\(y=\sqrt{3-\frac{3}{4}x^2}\)的图像是椭圆\(\cfrac{x^2}{4}-\cfrac{y^2}{3}=1\)的上半部分,
函数\(y=x+m\)的图像是动态的直线,
在同一个坐标系中做出两个函数的图像,由图像可知,
由图可知,直线和椭圆相交的一个位置是过点\((2,0)\),代入求得\(m=-2\);
另一个相交的临界位置是直线和函数\(y=f(x)=\sqrt{3-\frac{3}{4}x^2}\)在第二象限的部分相切,
设切点坐标\((x_0,y_0)\),
则有\(f'(x)=[(3-\frac{3}{4}x^2)^{\frac{1}{2}}]'=\frac{1}{2}\cdot (3-\frac{3}{4}x^2)^{-\frac{1}{2}}\cdot (3-\frac{3}{4}x^2)'\)
\(=\frac{1}{2}\cdot \frac{1}{\sqrt{3-\frac{3}{4}x^2}}\cdot (-\frac{3}{4}\cdot (2x))\)
\(= \frac{1}{\sqrt{3-\frac{3}{4}x^2}}\cdot (-\frac{3x}{4})\)
则\(f'(x_0)=\frac{-\frac{3x}{4}}{\sqrt{3-\frac{3}{4}x^2}}=1(x_0<0)\)
即\(-\frac{3x}{4}=\sqrt{3-\frac{3}{4}x^2}\),两边平方整理得到,
\(x_0^2=\frac{16}{7}\),即\(x_0=-\frac{4}{\sqrt{7}}\),
代入函数\(y=f(x)=\sqrt{3-\frac{3}{4}x^2}\),得到\(y_0=\frac{3}{\sqrt{7}}\)
即切点为\((-\frac{4}{\sqrt{7}},\frac{3}{\sqrt{7}})\)
将切点代入直线,得到\(m=\sqrt{7}\),
结合图像可知\(m\)的取值范围是\([\sqrt{7},2]\)。
【点评】:①本题目的难点一是将数的问题转化为形的问题求解,其中转化得到半个椭圆也是难点。
②难点二是求直线和椭圆相切时的切点坐标,求导很容易出错的,需要特别注意。
三、曲线和曲线相切
A、\(k>\cfrac{e}{2}\) \(\hspace{2cm}\) B、\(0< k<\sqrt{e}\) \(\hspace{2cm}\) C、\(k>\cfrac{\sqrt{2}e}{2}\) \(\hspace{2cm}\) D、 \(0< k<\cfrac{1}{2e}\)
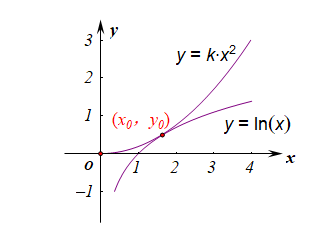
【法1】:数形结合法,定义域为\((0,+\infty)\),转化为方程\(kx^2=lnx\)有两个不同的实数根,
再转化为函数\(y=kx^2\)与函数\(y=lnx\)的图像有两个不同的交点,
如图设两个函数的图像相切于点为\((x_0,y_0)\),
则有关系式\(\begin{cases}2kx_0=\cfrac{1}{x_0}\\kx_0^2=y_0\\y_0=lnx_0\end{cases}\),
解得\(y_0=\cfrac{1}{2},x_0=\sqrt{e}\),即切点为\((\sqrt{e},\cfrac{1}{2})\),
再代入函数\(y=kx^2\),求得此时的\(k=\cfrac{1}{2e}\),
再结合函数\(y=kx^2\)的系数\(k\)的作用,可得两个函数要有两个不同的交点,
则\(k\in(0,\cfrac{1}{2e})\)。
【法2】:分离参数法,定义域为\((0,+\infty)\),转化为方程\(kx^2=lnx\)有两个不同的实数根,
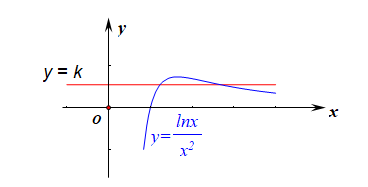
再转化为\(k=\cfrac{lnx}{x^2}\)有两个不同的实数根,
再转化为函数\(y=k\)和函数\(y=g(x)=\cfrac{lnx}{x^2}\)的图像有两个不同的交点,
用导数研究函数\(g(x)\)的单调性,\(g'(x)=\cfrac{\cfrac{1}{x}\cdot x^2-lnx\cdot 2x}{(x^2)^2}=\cfrac{1-2lnx}{x^3}\),
令\(1-2lnx>0\),得到\(0< x<\sqrt{e}\),令\(1-2lnx<0\),得到\(x >\sqrt{e}\),
即函数\(g(x)\)在区间\((0,\sqrt{e}]\)上单调递增,在\([\sqrt{e},+\infty)\)上单调递减,
故\(g(x)_{max}=g(\sqrt{e})=\cfrac{1}{2e}\),
作出函数\(g(x)\)和函数\(y=k\)的简图,由图像可得\(k\)的取值范围是\(k\in(0,\cfrac{1}{2e})\)。
四、直线和函数相切
(1)若直线\(y=kx+1\)与\(f(x)=lnx\)的图象相切.求实数\(k\)的值;
【解答】
(1)设直线和函数图像相切于点\((x_0,y_0)\),
则有\(\left\{\begin{array}{l}{y_0=kx_0+1①}\\{y_0=lnx_0②}\\{\cfrac{1}{x_0}=k③}\end{array}\right.\)
由③得到\(kx_0=1\),代入①得\(y_0=2\),代入②得到\(x_0=e^2\)
解得切点为\((e^2,2)\),将切点代入直线得到,\(k=\cfrac{1}{e^2}\)。
五、典例剖析
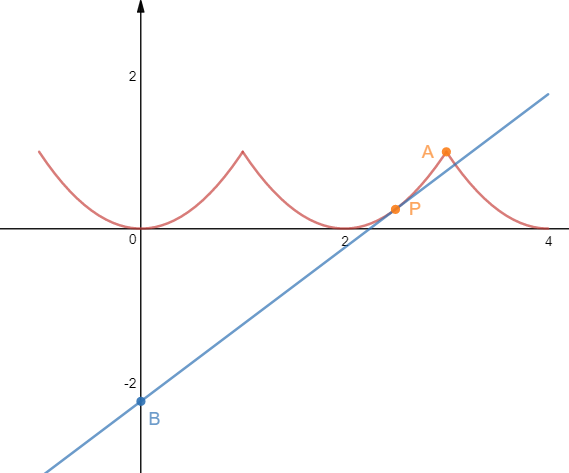
【分析】涉及到动直线和分段函数图像的交点个数问题,我们更多的是从形的角度入手分析,做出分段函数的图像和动直线的图像,通过动态的变化中寻找解题的题眼。本题目中就是\(k_{BP}<k<k_{BA}\)。
【解答】由\(x∈[0,1]\)时,\(f(x)=x^2\),以及\(f(x)=f(-x)\)可知,
当\(-1\leq x\leq 1\)时,\(f(x)=x^2\),
又由\(f(x)=f(2-x)\),可知函数\(f(x)\)图像关于直线\(x=1\)对称,
故当\(1\leq x\leq 3\)时,\(-3\leq -x\leq -1\),
则\(-1\leq 2-x\leq 1\),\(f(x)=f(2-x)=(2-x)^2=(x-2)^2\),
即\(1\leq x\leq 3\)时,\(f(x)=(x-2)^2\),
同理可知,当\(3\leq x\leq 4\)时,\(f(x)=(x-4)^2\),
又直线恒过过点\((0,-\cfrac{9}{4})\),故其方程为\(y+\cfrac{9}{4}=k(x-0)\),
即\(y=kx-\cfrac{9}{4}\),
做出函数\(f(x)\)当\(0\leq x\leq 4\)时的函数图像和\(y=kx-\cfrac{9}{4}\),
由图像可知,适合题意的\(k\)的范围是\(k_{BP}<k<k_{BA}\),
以下关键是求\(k_{BA}\)和\(k_{BP}\),
设直线和函数在\(x\in[2,3]\)相切于点\(P(x_0,y_0)\),
则\(\left\{\begin{array}{l}{k=2x_0-4①}\\{y_0=kx_0-\cfrac{9}{4}②}\\{y_0=(x_0-2)^2③}\end{array}\right.\)
将②代入③,得到\(kx_0-\cfrac{9}{4}=x_0^2-4x_0+4④\),
再将①代入④得到,\((2x_0-4)x_0-\cfrac{9}{4}=x_0^2-4x_0+4\)
解得\(x_0^2=\cfrac{25}{4}\),故\(x_0=\cfrac{5}{2}(舍去负值)\)。
将\(x_0=\cfrac{5}{2}\)代入①,得到\(k=k_{BP}=1\),
又由题可知点\(A(3,1)\),代入直线\(y=kx-\cfrac{9}{4}\),
得到\(k=k_{BA}=\cfrac{13}{12}\),
故适合题意的\(k\)的取值范围是\((1,\cfrac{13}{12})\)。
【点评】①注意总结利用奇偶性对称性求函数的解析式。②注意分段函数的图像画法;③求曲线的切线的思路和方法。④运用动态的观点和方法分析解决问题的策略。