此文章主要是结合哔站shuhuai008大佬的白板推导视频:变分自编码器_44min
全部笔记的汇总贴:机器学习-白板推导系列笔记
涉及到变分推断和重参数化技巧的内容,建议回顾一下白板推导系列笔记(十二)-变分推断
一、模型表示
VAE实质是一个隐变量模型(Latent Variable Model),我们通过GMM(混合高斯模型)来对比。
| GMM | VAE |
|---|---|
| k k k个高斯分布混合 | 无限个高斯分布的混合 |
| z ∼ C a t e g o r i c a l D i s t z\sim Categorical\;Dist z∼CategoricalDist | z ∼ N ( 0 , I ) P θ ( x / z ) ∼ N ( μ θ ( z ) , Σ θ ( z ) ) z\sim N(0,I)\;\;\;P_\theta(x/z)\sim N(\mu_\theta(z),\Sigma_\theta(z)) z∼N(0,I)Pθ(x/z)∼N(μθ(z),Σθ(z)) |
所以VAE的分布为:
P θ ( x ) = ∫ z P θ ( x , z ) d z = ∫ z P θ ( z ) ⋅ P θ ( x ∣ z ) d z P_\theta(x)=\int_z P_\theta(x,z){d}z=\int_z P_\theta(z)\cdot P_\theta(x|z){d}z Pθ(x)=∫zPθ(x,z)dz=∫zPθ(z)⋅Pθ(x∣z)dz
这个 P θ ( x ) P_\theta(x) Pθ(x)是intractable的,又因为 P θ ( z ∣ x ) = P θ ( z ) ⋅ P θ ( x ∣ z ) P θ ( x ) P_\theta(z|x)=\frac{P_\theta(z)\cdot P_\theta(x|z)}{P_\theta(x)} Pθ(z∣x)=Pθ(x)Pθ(z)⋅Pθ(x∣z),所以它也是intractable的。
Categorical Dist:
| z z z | 1 | 2 | ⋯ \cdots ⋯ | k k k |
|---|---|---|---|---|
| p p p | p 1 p_1 p1 | p 2 p_2 p2 | ⋯ \cdots ⋯ | p k p_k pk |
∑ i = 1 K p i = 1 x ∣ z = i ∼ N ( x ∣ μ i , Σ i ) \sum_{i=1}^K p_i=1\;\;\;\;\;\;\;\;\;\;x|z=i\sim N(x|\mu_i,\Sigma_i) ∑i=1Kpi=1x∣z=i∼N(x∣μi,Σi)
二、推断学习
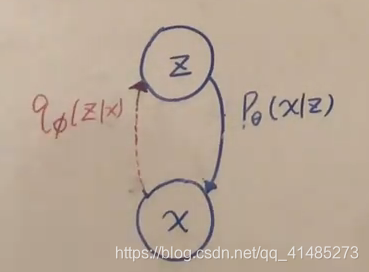
P ( z ) = N ( 0 , I ) P(z)=N(0,I) P(z)=N(0,I)
P θ ( x ∣ z ) = N ( μ θ ( z ) , Σ θ ( z ) ) P_\theta(x|z)= N(\mu_\theta(z),\Sigma_\theta(z)) Pθ(x∣z)=N(μθ(z),Σθ(z))
P θ ( z ∣ x ) i s i n t r a c t a b l e 我 们 用 q ϕ ( z ∣ x ) 来 逼 近 它 P_\theta(z|x) \;is\;intractable\;\;我们用q_\phi(z|x)来逼近它 Pθ(z∣x)isintractable我们用qϕ(z∣x)来逼近它
回顾一下EM:
log P ( x ) = E L B O + K L ( q ϕ ( z ∣ x ) ∣ ∣ p θ ( z ∣ x ) ) \log P(x)=ELBO+KL(q_\phi(z|x)||p_\theta(z|x)) logP(x)=ELBO+KL(qϕ(z∣x)∣∣pθ(z∣x))
E-Step:当 q = p θ ( z ∣ x ) q=p_\theta(z|x) q=pθ(z∣x)时,KL=0,expectation is ELBO
M-Step: θ = arg max E L B O = arg max E p θ ( z ∣ x ) [ log p θ ( x , z ) ] \theta=\argmax ELBO=\argmax E_{p_\theta(z|x)}[\log p_\theta(x,z)] θ=argmaxELBO=argmaxEpθ(z∣x)[logpθ(x,z)]
所以,
< θ ^ , ϕ ^ > = arg min K L ( q ϕ ( z ∣ x ) ∣ ∣ p θ ( z ∣ x ) ) = arg max E L B O = arg max E q ϕ ( z ∣ x ) [ log p θ ( x , z ) ] + H [ q ϕ ] = arg max E q ϕ ( z ∣ x ) [ log ( p θ ( x ∣ z ) + p θ ( z ) ) ] + H [ q ϕ ] = arg max E q ϕ ( z ∣ x ) [ log p θ ( x ∣ z ) ] − K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ) ) <\hat \theta,\hat\phi>=\argmin KL(q_\phi(z|x)||p_\theta(z|x))\\=\argmax ELBO\\=\argmax E_{q_\phi(z|x)}[\log p_\theta(x,z)] +H[q_\phi]\\=\argmax E_{q_\phi(z|x)}[\log (p_\theta(x|z)+p_\theta(z))] +H[q_\phi]\\=\argmax E_{q_\phi(z|x)}[\log p_\theta(x|z)] -KL(q_\phi(z|x)||p(z)) <θ^,ϕ^>=argminKL(qϕ(z∣x)∣∣pθ(z∣x))=argmaxELBO=argmaxEqϕ(z∣x)[logpθ(x,z)]+H[qϕ]=argmaxEqϕ(z∣x)[log(pθ(x∣z)+pθ(z))]+H[qϕ]=argmaxEqϕ(z∣x)[logpθ(x∣z)]−KL(qϕ(z∣x)∣∣p(z))
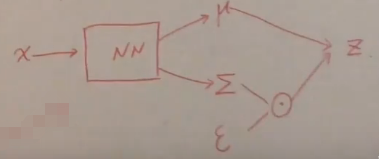
采用SGVI/SGVB/SVI/Amortized Inference,也就是利用神经网络和重参数化技巧来解决这个优化问题。
ε ∼ N ( 0 , I ) z ∣ x ∼ N ( μ ϕ ( x ) , Σ ϕ ( x ) ) \varepsilon \sim N(0,I)\\z|x\sim N(\mu_\phi(x),\Sigma_\phi(x)) ε∼N(0,I)z∣x∼N(μϕ(x),Σϕ(x))
z = μ ϕ ( x ) + Σ ϕ 1 2 ( x ) ⋅ ε z=\mu_\phi(x)+\Sigma_\phi^{\frac12}(x)\cdot\varepsilon z=μϕ(x)+Σϕ21(x)⋅ε
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;
\;
\;
\;
\;
下一章传送门:白板推导系列笔记(三十三)-流模型