文章目录
0 笔记说明
来源于【机器学习】【白板推导系列】【合集 1~23】,我在学习时会跟着up主一起在纸上推导,博客内容为对笔记的二次书面整理,根据自身学习需要,我可能会增加必要内容。
注意:本笔记主要是为了方便自己日后复习学习,而且确实是本人亲手一个字一个公式手打,如果遇到复杂公式,由于未学习LaTeX,我会上传手写图片代替(手机相机可能会拍的不太清楚,但是我会尽可能使内容完整可见),因此我将博客标记为【原创】,若您觉得不妥可以私信我,我会根据您的回复判断是否将博客设置为仅自己可见或其他,谢谢!
本博客为(系列七)的笔记,对应的视频是:【(系列七) 核方法1-背景介绍】、【(系列七) 核方法2-正定核-两个定义】、【(系列七) 核方法3-正定核-必要性证明】。
下面开始即为正文。
有三个概念:① 思想角度上:核方法(Kernel Method);② 计算角度上:核技巧(Kernel Trick);③ 核函数(Kernel Function)。
1 背景介绍
现实中的问题大多是非线性可分的。举个栗子,线性可分是这样的——比如一条笔直的河将两岸的事物一分为二,这样的话,这条笔直的河作为一个“超平面”就将事物分为两类了。但是现实中没有哪条河是笔直不曲的,再举个其他的栗子——区域划分就是非线性可分的,每个省之间不是由一条直线就分开了的,是由一条弯弯曲曲的线隔开的。可以这样理解,若样本集可由一条直线直接划分为两类的就是线性可分问题,其他情况就是非线性可分问题。
1.1 Cover定理
怎么处理非线性可分问题呢?可以将低维的样本集转换到高维空间,转换后的样本集就有可能是线性可分的了。Cover定理:将复杂分类问题非线性地映射到高维空间将比映射到低维空间更可能是线性可分的。
下面举个栗子。
1.2 异或问题
对于异或问题,设集合D={0,1},输入空间为X={(0,0),(1,1),(0,1),(1,0)},显然输入空间是二维的,在坐标轴上表示为:
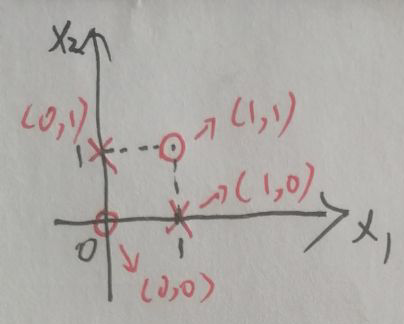
输入空间X中有四个点。对于异或问题,x1与x2相同为0不同为1,因此X中前两个点的值为0(图中用o表示),后两个点的值为1(图中用×表示)。显然没有一条直线可以解决异或问题的分类。

现在做这样的处理:对于输入空间中的任一点(x1,x2),转换为(x1,x2,(x1-x2)2),称转换后的空间为特征空间,记为Z,则Z={(0,0,0),(1,1,0),(0,1,1),(1,0,1)}。显然特征空间是三维的,在坐标轴上表示为:
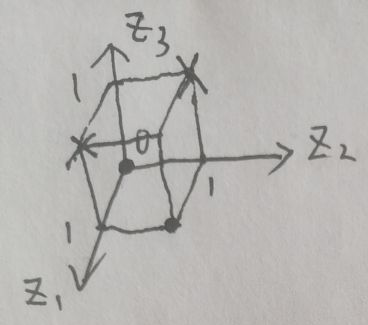
特征空间Z中有四个点,前两个点的值为0(图中用o表示),均在底平面;后两个点的值为1(图中用×表示),均在顶平面。显然,任意一个在底平面和顶平面之间的平面可以解决异或问题的分类。
2 正定核
2.1 核函数
设集合X为输入空间,其中每个样本均是n维的。从X中任意取两个样本x与z,即x、z∈Rn。K是一个将X×X映射到R上的映射,即K:X×X→R,称K(x,z)为核函数。
2.2 正定核函数
不说明的情况下,核函数指的就是正定核函数。什么是正定核函数呢?有两种定义,如下:
2.2.1 定义1
若存在希尔伯特空间(【3 希尔伯特空间】一节中会解释)中的某个非线性映射φ,φ实现了从输入空间X到特征空间Z的映射,其中Z∈Rm,m远大于n,即n<<m。若有K(x,z)=<φ(x),φ(z)>,其中<φ(x),φ(z)>表示φ(x)与φ(z)的内积运算,即K(x,z)=φ(x)Tφ(z),则称K(x,z)为正定核函数。
2.2.2 定义2
若K(x,z)满足:① 对称性;② 正定性,则称K(x,z)为正定核函数。其中:
① 对称性:K(x,z)=K(z,x);
② 正定性:从输入空间X中任取N个元素x1,x2,…,xN,对应的Gram矩阵为正定的。Gram矩阵G=[K(xi,xj)]。
3 希尔伯特空间
完备的、可能是无限维的、定义了内积运算的线性空间称为希尔伯特空间。
3.1 完备
柯西序列是这样一个序列——它的元素随着序数的增加而愈发靠近。更确切地说,在去掉有限个元素后,可以使得余下的元素中任何两点间的距离的最大值不超过任意给定的正数。
完备空间是这样的空间——空间中的任何柯西序列都收敛在该空间之内。举个栗子,对空间中的任意一个序列:{k1,k2,…,kn},若该系列是收敛的,即有:

若k仍然在该空间中,则称该空间为完备空间。
3.2 无限维
希尔伯特空间的维度可以是无限大的。
3.3 内积
设V是实数域R上的n维线性空间,对V中的任意两个向量α、β依一确定法则对应着一个实数,这个实数称为内积,记做<α,β>。并且要求内积运算满足下列四个条件,其中α、β、v是V中任意一个向量。:
(1)<α,β>=<β,α>;
(2)<kα,β>=k<α,β>,其中k为任意实数;
(3)<α+β,v>=(α,v)+(β,v);
(4)<α,α>≥0,当且仅当α=0时<α,α>=0。
3.4 线性空间
V是非空集合,F是数域,若在其上定义了加法和数乘运算,且满足八条法则,则称集合V为数域F上的线性空间。
4 必要性证明
【2.2 正定核函数】一节中的定义1是正定核函数的本质定义,现在证明从定义1可以推出定义2,下面是证明过程:
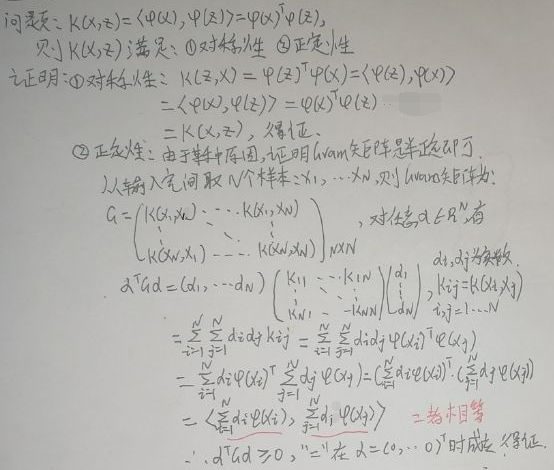
由上述证明过程可知,定义1可以推出定义2。
5 核函数的性质
(1)核函数的引入避免了“维数灾难”,大大减小了计算量。而输入空间的维数n对Gram矩阵无影响,因此,核函数方法可以有效处理高维输入。
(2)无需知道非线性变换函数φ的形式和参数。
(3)核函数的形式和参数的变化会隐式地改变从输入空间X到特征空间Z的映射,进而对特征空间的性质产生影响,最终改变各种核函数方法的性能。
(4)核方法(Kernel Method)可以和不同的算法相结合,形成多种不同的基于核技巧(Kernel Trick)的方法,且这两部分的设计可以单独进行,并可以为不同的应用选择不同的核函数和算法,如Kernel SVM,即核SVM(请看此博文)。
END