文章目录
0 笔记说明
来源于【机器学习】【白板推导系列】【合集 1~23】,我在学习时会跟着up主一起在纸上推导,博客内容为对笔记的二次书面整理,根据自身学习需要,我可能会增加必要内容。
注意:本笔记主要是为了方便自己日后复习学习,而且确实是本人亲手一个字一个公式手打,如果遇到复杂公式,由于未学习LaTeX,我会上传手写图片代替(手机相机可能会拍的不太清楚,但是我会尽可能使内容完整可见),因此我将博客标记为【原创】,若您觉得不妥可以私信我,我会根据您的回复判断是否将博客设置为仅自己可见或其他,谢谢!
本博客为(系列八)的笔记,对应的视频是:【(系列八) 指数族分布1-背景】、【(系列八) 指数族分布2-背景续】、【(系列八) 指数族分布3-高斯分布的指数族形式】、【(系列八) 指数族分布4-对数配分函数与充分统计量】、【(系列八) 指数族分布5-极大似然估计与充分统计量】、【(系列八) 指数族分布6-最大熵角度(1)】、【(系列八) 指数族分布7-最大熵角度(2)】。
下面开始即为正文。
1 背景
对于给定的统计问题,包含原样本中关于该问题的全部有用信息的统计量称为充分统计量。对于未知参数的估计问题,保留了原始样本中关于未知参数θ的全部信息的统计量,就是充分统计量。
1.1 指数族分布的一般形式
指数族分布是这样一种类型的分布,其形式为:
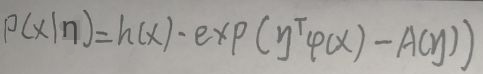
上图中,x属于Rp,h(x)为关于x的函数,有时令其为1即可(在【2 高斯分布的指数族形式】一节会提到),η的类型为向量,η与具体问题的参数θ有关,φ(x)称作充分统计量,A(η)称作对数配分函数,下图解释了为什么A(η)称作对数配分函数:

指数族分布包括有:高斯分布、类别分布、多项式分布、泊松分布、贝塔分布、狄利克雷分布、伽玛分布等,它们都属于指数族分布。
1.2 共轭先验
对于公式:
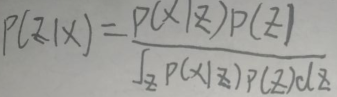
P(z)是先验概率,即没有训练数据x前,通过经验或分析得到z的概率。P(x|z)是似然函数。P(z|x)是后验概率,属于条件概率,即在有了训练数据x的情况下z发生的概率。
共轭先验指的是:若先验概率的分布和后验概率的分布有相同的形式,那么就称先验的分布与似然函数是共轭的。共轭的结果是让先验与后验具有相同的形式,只是参数不同。
2 高斯分布的指数族形式
本节针对的是一维高斯分布。首先设参数θ=(μ,σ2),下图将一维高斯分布的密度函数改为指数族分布公式的形式:
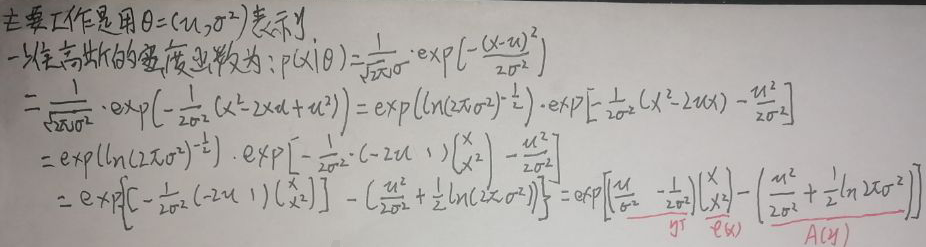
更进一步地:

根据【1.1 指数族分布的一般形式】一节第一张图片,这里h(x)=1,另外η、φ(x)、A(η)由上图给出,于是就把一维高斯分布的密度函数改为了指数族分布的形式。
3 对数配分函数与充分统计量
在指数族分布的公式中,φ(x)称作充分统计量,A(η)称作对数配分函数。下面研究A(η)与φ(x)的关系:

对①式的左右两边关于η求偏导:

根据上图有:
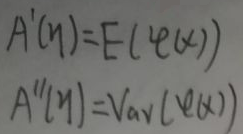
对数配分函数A(η)与充分统计量φ(x)的关系为:① A(η)关于η的一阶导数等于φ(x)的期望;② A(η)关于η的二阶导数等于φ(x)的方差。
4 极大似然估计与充分统计量
下面研究使用MLE研究充分统计量φ(x)和η。首先假定样本集为X=(x1,x2,…,xN),设xi为离散型随机变量,使用MLE求η:
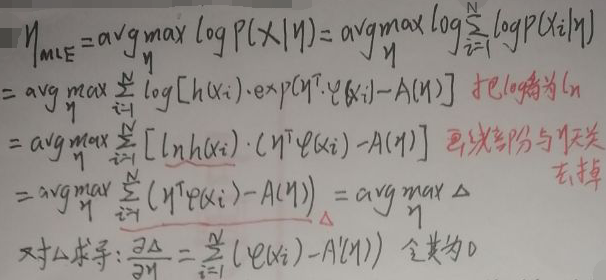
接着有:
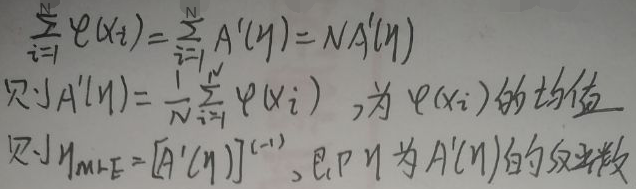
由上图得:使用极大似然估计后,A(η)关于η的一阶导数等于充分统计量φ(x)的均值;参数η等于A(η)的一阶导数的反函数。
5 熵
设事件x发生的概率为p(x),则信息量为-log p(x),即信息量与概率成反比例关系。熵是对随机变量包含的信息量和不确定性的衡量,大小等于信息量的期望,所以熵的公式为:
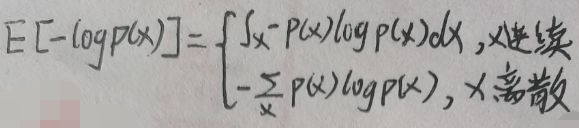
5.1 最大熵⇔x服从均匀分布
本节证明最大熵⇔x服从均匀分布。假设x是离散的,下面是证明过程:

因此,最大熵⇔x服从均匀分布得证。
5.2 最大熵原理
根据【5.1 最大熵⇔x服从均匀分布】一节的结论,最大熵是对等可能性的定量描述。最大熵原理指包含已知的经验、事实和信息,不做任何未知假设,把未知事件当成等概率事件处理。
已知的经验、事实和信息是什么呢?举个栗子,假定数据集D=(x1,x2,…,xN),设X为离散型随机变量,且X服从经验分布,即:
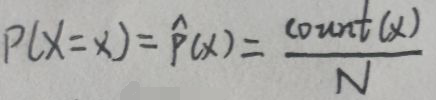
上图中,count(x)指数据集D中xi=x的样本个数。根据上述公式,可以求出期望E(X)和方差Var(X),但是这里重点不是这个,所以不会花时间去求。总之,有了数据集D后,其期望E(X)和方差Var(X)可以看作是已知的事实。设f(x)是任意一个自变量为x的函数,则E(f(x))也是可求的,因此也可以将其看作是已知的事实。这样就将已知的经验、事实和信息转换为数学量——期望和方差了。
现在要求的是使熵最大的x的分布p(x),设x为离散型随机变量,下面是详细过程:
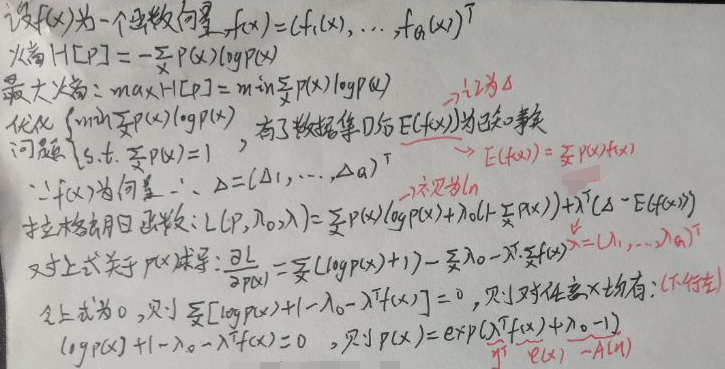
对照【1.1 指数族分布的一般形式】一节第一张图片,看上图的右下角:令η=(λ0,λ)T,φ(x)=f(x),A(η)=1-λ0,h(x)=1。
综上所述,使熵最大的x的分布p(x)是指数族分布。
END