此文章主要是结合哔站shuhuai008大佬的白板推导视频:马尔科夫决策过程_107min
全部笔记的汇总贴:机器学习-白板推导系列笔记
一、背景介绍
Random Variable: X Y X ⊥ Y X\;\;Y\;\;X\bot Y XYX⊥Y
Stochastic Process: { S t } t = 1 ∞ \{S_t\}_{t=1}^\infty {
St}t=1∞
Markov Chain/Process,具有Markov Property的随机过程: P ( S t + 1 ∣ S t , S t − 1 , ⋯ , S 1 ) = P ( S t + 1 ∣ S t ) P(S_{t+1}|S_t,S_{t-1},\cdots,S_1)=P(S_{t+1}|S_t) P(St+1∣St,St−1,⋯,S1)=P(St+1∣St)
State Space Model:(HMM,Kalman Filter,Particle Filter)Markov Chain+Observation
Markov Reward Process:Markov Chain+Reward
Markov Decision Process:Markov Chain+Reward+Action
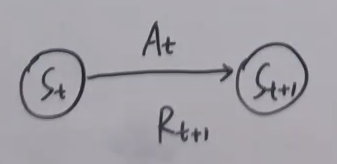
S : s t a t e s e t → S t A : a c t i o n s e t , ∀ s ∈ S , A ( s ) → A t R : r e w a r d s e t → R t , R t + 1 S:state\;set\rightarrow S_t\\A:action\;set,\forall s\in S,A(s)\rightarrow A_t\\R:reward\;set\rightarrow R_t,R_{t+1} S:stateset→StA:actionset,∀s∈S,A(s)→AtR:rewardset→Rt,Rt+1
二、动态特性
Markov Chain: S S S
MRP: S , R S,R S,R
MDP: S , A ( s ) , R , P ( 动 态 特 性 ) S,A(s),R,P(动态特性) S,A(s),R,P(动态特性)

P : p ( s ′ , r ∣ s , a ) ≜ P r { S t + 1 = s ′ , R t + 1 = r ∣ S t = s , A t = a } P:p(s',r|s,a)\triangleq Pr\{S_{t+1}=s',R_{t+1}=r|S_t=s,A_t=a\} P:p(s′,r∣s,a)≜Pr{
St+1=s′,Rt+1=r∣St=s,At=a}
状态转移函数:
P ( s ′ ∣ s , a ) ∑ r ∈ R P ( s ′ , r ∣ s , a ) P(s'|s,a)\sum_{r\in R}P(s',r|s,a) P(s′∣s,a)r∈R∑P(s′,r∣s,a)
三、价值函数

Policy: π \pi π表示
- 确定性策略: a ≜ π ( s ) a\triangleq \pi(s) a≜π(s)
- 随机性策略: π ( a ∣ s ) ≜ P r { A t = a ∣ S t = s } \pi(a|s)\triangleq Pr\{A_t=a|S_t=s\} π(a∣s)≜Pr{ At=a∣St=s}
回报:
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ + γ r − 1 R T = ∑ i = 0 ∞ γ i R t + i + 1 ( T → ∞ ) γ ∈ [ 0 , 1 ] G_t=R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\cdots+\gamma^{r-1}R_T=\sum_{i=0}^{\infty}\gamma^iR_{t+i+1}\;\;(T\rightarrow\infty) \\\gamma\in [0,1] Gt=Rt+1+γRt+2+γ2Rt+3+⋯+γr−1RT=i=0∑∞γiRt+i+1(T→∞)γ∈[0,1]
价值函数: V π ( s ) ≜ E π [ G t ∣ S s = s ] q π ( s , a ) ≜ E π [ G t ∣ S s = s , A t = a ] V_\pi(s)\triangleq E_{\pi}[G_t|S_s=s]\\q_\pi(s,a)\triangleq E_{\pi}[G_t|S_s=s,A_t=a] Vπ(s)≜Eπ[Gt∣Ss=s]qπ(s,a)≜Eπ[Gt∣Ss=s,At=a]
四、贝尔曼期望方程
回溯图:

Value Function: V π ( s ) ≜ E π [ G t ∣ S s = s ] ( 加 权 平 均 值 ) q π ( s , a ) ≜ E π [ G t ∣ S s = s , A t = a ] V_\pi(s)\triangleq E_{\pi}[G_t|S_s=s](加权平均值)\\q_\pi(s,a)\triangleq E_{\pi}[G_t|S_s=s,A_t=a] Vπ(s)≜Eπ[Gt∣Ss=s](加权平均值)qπ(s,a)≜Eπ[Gt∣Ss=s,At=a]
V π ( s ) = ∑ a ∈ A ( s ) π ( a ∣ s ) ⋅ q π ( s , a ) V_\pi(s)=\sum_{a\in A(s)}\pi(a|s)\cdot q_\pi(s,a) Vπ(s)=a∈A(s)∑π(a∣s)⋅qπ(s,a)
V π ( s ) = π ( a 1 ∣ s ) ⋅ q π ( s . a 1 ) V_\pi(s)=\pi(a_1|s)\cdot q_\pi(s.a_1) Vπ(s)=π(a1∣s)⋅qπ(s.a1)
q π ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) ⋅ [ r + γ V π ( s ′ ) ] q_\pi(s,a)=\sum_{s',r}p(s',r|s,a)\cdot[r+\gamma V_\pi(s')] qπ(s,a)=s′,r∑p(s′,r∣s,a)⋅[r+γVπ(s′)]
贝尔曼期望方程:
V π ( s ) = ∑ a ∈ A π ( a ∣ s ) ⋅ ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V π ( s ′ ) ] V_\pi(s)=\sum_{a\in A}\pi(a|s)\cdot\sum_{s',r}p(s',r|s,a)[r+\gamma V_\pi(s')] Vπ(s)=a∈A∑π(a∣s)⋅s′,r∑p(s′,r∣s,a)[r+γVπ(s′)]
V π ( s ) = E π [ R t + 1 + γ V π ( S t + 1 ) ∣ S t = s ] V_\pi(s)=E_\pi\Big[R_{t+1}+\gamma V_\pi(S_{t+1})|S_t=s\Big] Vπ(s)=Eπ[Rt+1+γVπ(St+1)∣St=s]
q π ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) ⋅ [ r + γ ∑ a ′ ∈ A π ( a ′ ∣ s ′ ) ⋅ q π ( s ′ , a ′ ) ] q_\pi(s,a)=\sum_{s',r}p(s',r|s,a)\cdot[r+\gamma \sum_{a'\in A}\pi(a'|s')\cdot q_\pi(s',a')] qπ(s,a)=s′,r∑p(s′,r∣s,a)⋅[r+γa′∈A∑π(a′∣s′)⋅qπ(s′,a′)]
五、贝尔曼最优方程
V ∗ ( s ) ≜ max π V π ( s ) q ∗ ( s , a ) ≜ max π q π ( s , a ) V_*(s)\triangleq \max_\pi V_\pi(s)\\q_*(s,a)\triangleq \max_\pi q_\pi(s,a) V∗(s)≜πmaxVπ(s)q∗(s,a)≜πmaxqπ(s,a)
记 π ∗ = arg max π V π ( s ) = arg max π q π ( s , a ) \pi_*=\argmax_\pi V_\pi(s)=\argmax_\pi q_\pi(s,a) π∗=πargmaxVπ(s)=πargmaxqπ(s,a),
V ∗ ( s ) = max π V π ( s ) = V π ∗ ( s ) q ∗ ( s , a ) = max π q π ( s , a ) = q π ∗ ( s , a ) V_*(s)= \max_\pi V_\pi(s)=V_{\pi_*}(s)\\q_*(s,a)= \max_\pi q_\pi(s,a)=q_{\pi_*}(s,a) V∗(s)=πmaxVπ(s)=Vπ∗(s)q∗(s,a)=πmaxqπ(s,a)=qπ∗(s,a)
V π ∗ ( s ) ≤ max a q π ∗ ( s , a ) V_{\pi_*}(s)\le\max_aq_{\pi_*}(s,a) Vπ∗(s)≤amaxqπ∗(s,a)
假如 V π ∗ ( s ) < max a q π ∗ ( s , a ) V_{\pi_*}(s)<\max_aq_{\pi_*}(s,a) Vπ∗(s)<amaxqπ∗(s,a)则可以构造一个 π n e w \pi_{new} πnew, π n e w ( s ) = arg max a q π ∗ ( s , a ) π n e w ( s ‾ ) = π ∗ ( s ‾ ) 或 π n e w ( a ∣ s ‾ ) = π ∗ ( a ∣ s ‾ ) \pi_{new}(s)=\argmax_a q_{\pi_*}(s,a)\\\pi_{new}(\overline{s})=\pi_{*}(\overline{s})或\pi_{new}(a|\overline{s})=\pi_{*}(a|\overline{s}) πnew(s)=aargmaxqπ∗(s,a)πnew(s)=π∗(s)或πnew(a∣s)=π∗(a∣s)
则, V π n e w ( s ) = max a q π ∗ ( s , a ) > V π ∗ ( s ) V_{\pi_{new}}(s)=\max_a q_{\pi_*}(s,a)>V_{\pi_*}(s) Vπnew(s)=amaxqπ∗(s,a)>Vπ∗(s)
则说明 π n e w \pi_{new} πnew好于 π ∗ \pi_* π∗,这与 π ∗ \pi_* π∗最优矛盾,因此假设不成立,所以有: V π ∗ ( s ) = max a q π ∗ ( s , a ) V_{\pi_*}(s)=\max_aq_{\pi_*}(s,a) Vπ∗(s)=amaxqπ∗(s,a)
V π ∗ ( s ) = max a q π ∗ ( s , a ) V_{\pi_*}(s)=\max_aq_{\pi_*}(s,a) Vπ∗(s)=amaxqπ∗(s,a)
V ∗ ( s ) = max a q ∗ ( s , a ) V_{*}(s)=\max_aq_{*}(s,a) V∗(s)=amaxq∗(s,a)
q ∗ ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) ⋅ [ r + γ V ∗ ( s ′ ) ] q_*(s,a)=\sum_{s',r}p(s',r|s,a)\cdot[r+\gamma V_*(s')] q∗(s,a)=s′,r∑p(s′,r∣s,a)⋅[r+γV∗(s′)]
贝尔曼最优方程:
V ∗ ( s ) = max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V ∗ ( s ′ ) ] V_*(s)=\max_a\sum_{s',r}p(s',r|s,a)[r+\gamma V_*(s')] V∗(s)=amaxs′,r∑p(s′,r∣s,a)[r+γV∗(s′)]
q ∗ ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) ⋅ [ r + γ max a ′ q ∗ ( s ′ , a ′ ) ] q_*(s,a)=\sum_{s',r}p(s',r|s,a)\cdot[r+\gamma \max_{a'} q_*(s',a')] q∗(s,a)=s′,r∑p(s′,r∣s,a)⋅[r+γa′maxq∗(s′,a′)]
\;
\;
\;
下一章传送门:白板推导系列笔记(三十五)-动态规划(强化学习)