机器学习-白板推导-系列（五）笔记：降维(PCA/SVD/PCoA/PPCA)

---

0 笔记说明

来源于【机器学习】【白板推导系列】【合集 1～23】，我在学习时会跟着up主一起在纸上推导，博客内容为对笔记的二次书面整理，根据自身学习需要，我可能会增加必要内容。

注意：本笔记主要是为了方便自己日后复习学习，而且确实是本人亲手一个字一个公式手打，如果遇到复杂公式，由于未学习LaTeX，我会上传手写图片代替（手机相机可能会拍的不太清楚，但是我会尽可能使内容完整可见），因此我将博客标记为【原创】，若您觉得不妥可以私信我，我会根据您的回复判断是否将博客设置为仅自己可见或其他，谢谢！

本博客为（系列五）的笔记，对应的视频是：【(系列五) 降维1-背景】、【(系列五) 降维2-样本均值&样本方差矩阵】、【(系列五) 降维3-PCA-最大投影方差】、【(系列五) 降维4-PCA-最小重构代价】、【(系列五) 降维5-SVD角度开看PCA和PCoA】、【(系列五) 降维6-主成分分析（PCA）-概率角度（Probabilistic PCA）】。

下面开始即为正文。

---

1 背景

降维是解决过拟合问题的方法之一。输入数据x的维度p过大会导致维数灾难，会造成数据稀疏等问题。降维有三种类型：

① 直接降维，如特征选择；

② 线性降维，如PCA（Principal component analysis，主成分分析），MDS（MultiDimensional Scaling，多维尺度变换）；

③ 非线性降维，如ISOMAP（Isometric Mapping，等距特征映射），LLE（locally linear embedding，局部线性嵌入降维算法）。

下面先讨论样本均值与样本方差矩阵。

数据集D中有N个样本实例，D = {(x₁, y₁), (x₂, y₂),…,(x_N, y_N)}。现在构造矩阵X = (x₁,x₂,…,x_N)^T，每个样本x_i∈R^p，i=1…N，X为N×p阶矩阵。构造N×1矩阵1_N=(1,1,…,1)^T，Ⅰ_N为N×N单位矩阵。

1.1 样本均值

样本均值（是p×1的向量）为：

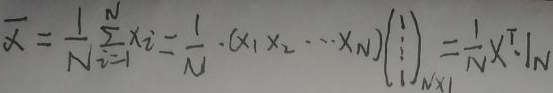
注意最右面是N×1矩阵1_N=(1,1,…,1)^T。

1.2 样本协方差矩阵

样本协方差矩阵（是p×p的矩阵）为：

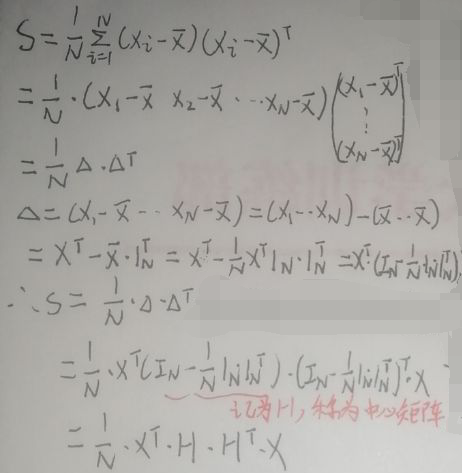
对于上图的矩阵H=Ⅰ_N-1/N·1_N·1_N^T，经过验证，H^T=H，H=H²=H³=…Hⁿ。因此S=1/N·X^T·H·H^T·X=1/N·X^T·H·H·X=1/N·X^T·H²·X=1/N·X^T·H·X。

最后，样本协方差矩阵为S=1/N·X^T·H·X。

---

2 主成分分析PCA

PCA先重构原始特征空间，之后从p维特征中选出q维特征（p≥q）。PCA的思想可以总结为——“一个中心，两个基本点”：

（1）一个中心：对原始特征空间重构；

（2）两个基本点：最大投影方差与最小重构距离。

2.1 最大投影方差

为方便计算，首先是中心化，将所有数据x_i平移到以原点为中心的区域，变为x_i-x杠，x杠是所有x_i的均值。先看看投影长度Δ（下图中提到的投影均是投影长度，是标量）怎么求：

数据x_i∈R^p，而PCA对原始特征空间重构，所以重构后的空间也应该是p维的，设这个p维空间的一组基为(u₁,u₂,…u_p)，且||u_i||=1，i=1…p。以p=2为例：

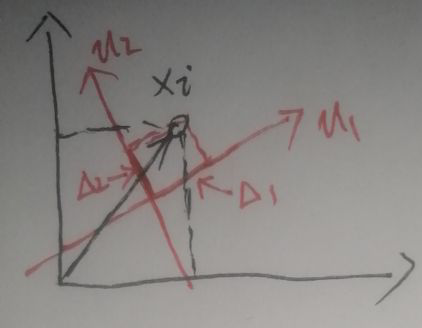
上图中，黑色坐标轴为原始空间，红色坐标轴为重构后的空间。假设x_i在上图的位置，在重构空间的坐标轴u₁、u₂上的投影长度分别为Δ₁、Δ₂。根据本节第一张图，Δ₁、Δ₂为：

上图最后一行实质是坐标变换。先看一个方向上的情况，这里以u₁方向为例（||u₁||=1）：

此时转变为最优化问题：

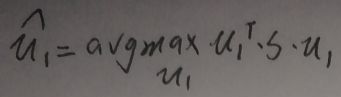
使用拉格朗日乘数法（我不太了解这种方法，我只是按up主说的写的而已，您可以看百度百科）——构造L(u₁,λ)，注意||u₁||=1=u₁^T·u₁：

是不是很熟悉，S为样本的协方差矩阵，是p×p的矩阵，这样不就是特征值与特征向量吗？——u₁为矩阵S对应于λ的单位特征向量。

那么新的重构空间的基就是样本的协方差矩阵的p个单位特征向量u₁,u₂,…u_p。

这真是太巧了，太棒了！

2.2 最小重构距离

样本x_i重构后为：

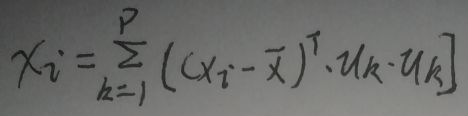
再从p维特征向量中选择q维特征向量（p≥q）后为：

定义N个数据x_i在q个维度上的代价距离为J：

现在要求的就是最小重构距离【min J】，因为重构后的p维空间的一组基为(u₁,u₂,…u_p)，且||u_k||=u_k^Tu_k=1，k=1…p，所以u₁,u₂,…u_p之间是线性无关的，而且两两之间正交，因此可以分别单独求每一个u_k^T·S·u_k的最小值，k=q+1,q+2,…p，最后将每一个最小值相加就是J的最小值。与【2.1 最大投影方差】一节的倒数第二张图片类似，只不过应该将max改为min，通过拉格朗日乘数法得到的结果也是类似的——【S·u_k=λ·u_k】，k=q+1,q+2,…p，在等式两边同左乘u_k^T得到【u_k^T·S·u_k=λ·u_k^T·u_k】，因为||u_k||=u_k^Tu_k=1，所以【u_k^T·S·u_k=λ】。注意到要求的是【每一个u_k^T·S·u_k的最小值】，而λ是协方差矩阵S的特征值，那么取其最小的p-q个特征值求和便是J的最小值。若将p个特征值从大到小排列，就是取从k=q+1到第p个特征值，即最小重构距离min J为：

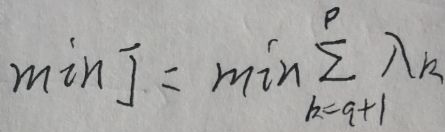
2.3 总结

PCA的步骤：

（1）拿到N个样本x_i后，构建矩阵X = (x₁,x₂,…,x_N)^T，每个样本x_i∈R^p，i=1…N，X为N×p阶矩阵。构造N×1矩阵1_N=(1,1,…,1)^T，Ⅰ_N为N×N单位矩阵。构建矩阵H=Ⅰ_N-1/N·1_N·1_N^T，根据【1.2 样本协方差矩阵】一节最后一行文字可得协方差矩阵（是p×p的哦）为S=1/N·X^T·H·X。求矩阵特征值与特征向量时与系数无关，所以去掉系数1/N，使S=X^T·H·X。因为协方差矩阵为对称矩阵，所以S^T=S。对S做特征分解（也称为谱分解），即S=UΛU^T，其中U为正交矩阵即U^TU=UU^T=Ⅰ_N，Λ是由S的p个特征值λ_i组成的矩阵，即Λ=diag(λ₁,λ₂,…,λ_p)，且λ₁＞λ₂＞…＞λ_p，则U的列向量从左到右依次为S的对应于λ_i的单位特征向量u_i，从这p个特征向量中挑选q个（q≤p），便称为PCA的主成分。

（2）将X中心化后的HX在主成分即q个方向上投影，即可求得对应坐标矩阵为HXV：

其中V是由挑出的q个特征向量组成的p×q矩阵，HXV为N×N×N×p×p×q=N×q的矩阵，而原来的X是N×p的，这里q≤p，这样就达到降维的目的。坐标矩阵HXV的行向量为N个降维后的样本，每个样本被降维为q维向量。

---

3 SVD分解HX

由N个样本x_i构建的矩阵X = (x₁,x₂,…,x_N)^T，为N×p阶矩阵，且每个样本x_i∈R^p，i=1…N。将X中心化后变为：

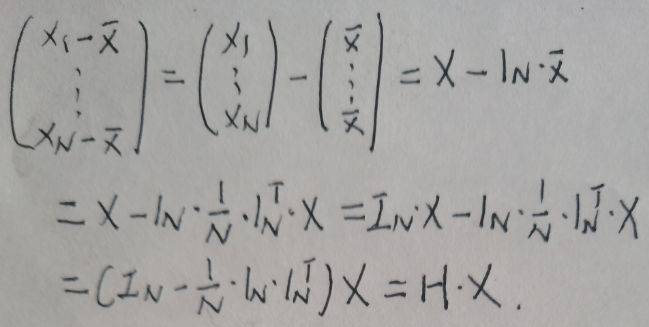
对H·X进行奇异值分解（SVD）得到：H·X=UΣV^T，U为N×N的矩阵，V为p×p的矩阵，U和V均为正交矩阵，即U^TU=UU^T=Ⅰ_N，V^TV=VV^T=Ⅰ_p。令【Δ₁=(H·X)·(H·X)^T，Δ₂=(H·X)^T·(H·X)】，矩阵Δ₁和Δ₂的正特征值的个数与大小均是完全相同的。Σ是N×p的矩阵，该矩阵在a_ii，即行数与列数相同的元素为上述正特征值的正平方根，并且从左到右按从大到小排列着。

对【2.3 总结】一节得到的坐标矩阵HXV=UΣV^TV=UΣ。

因为S=1/N·X^T·H·X，H^T=H，H=H²=H³=…Hⁿ，所以S=1/N·X^T·H^T·H·X。又因为求矩阵特征值与特征向量时与系数无关，所以去掉系数1/N，使S=X^T·H^T·H·X。代入H·X=UΣV^T得：S=(UΣV^T)^TUΣV^T=VΣ^TU^TUΣV^T，因为U^TU=UU^T=Ⅰ_N，所以S=VΣ^TΣV^T，其中Σ^TΣ为p×p的矩阵，除对角线元素外均为0，对角线上的非零元素为矩阵Δ1和Δ2的正特征值。这样就不用专门求协方差矩阵S，通过运算就能得到S：① 对X中心化后变为H·X；② 对H·X进行SVD分解：H·X=UΣV^T；③ S=VΣ^TΣV^T。最后就得到协方差矩阵S了。

---

4 主坐标分析PCoA

主坐标分析（Principal Co-ordinates Analysis，PCoA）是这样的：先构造T=H·X·X^T·H=H·X·X^T·H^T，则T=UΣV^T·(UΣV^T)^T=UΣV^T·VΣ^TU^T=UΣΣ^TU^T，即T=UΣΣ^TU^T，等式两边同右乘UΣ得：TUΣ=UΣΣ^TU^TUΣ=UΣΣ^TΣ，即TUΣ=UΣΣ^TΣ，其中Σ^TΣ是由T的特征值组成的对角矩阵，UΣ由Σ^TΣ的对角线元素即T的特征值对应的特征向量组成。

也就是说，对PCoA构造的T进行特征分解（或称谱分解）可直接得到坐标矩阵UΣ，由T的特征值对应的特征向量组成。

同时，要注意到S是p×p的矩阵，T是N×N的矩阵。当维度p很高时，求S就比较困难，可以转而使用PCoA的T矩阵。

---

5 概率主成分分析PPCA

概率主成分分析PPCA（Probabilitic PCA）是从概率角度出发的PCA。

将原始数据（也称为observed data，即可观测数据）x_i∈R^p降维到z_i∈R^q（z_i称为latent data，即潜数据）。z_i与x_i均为连续型向量。

PPCA有三点假设：① 潜数据z～N(0,Ⅰ_q)，其中0是q×1的向量,Ⅰ_q是q×q的单位矩阵；② 噪声ε～N(0,δ²·Ⅰ_p)，其中0是p×1的向量，δ²·Ⅰ_p是对角线上元素都是δ²的对角矩阵，是p×p的矩阵，注意ε与z相互独立；③ 可观测数据x=w·z+μ+ε，w是p×q的矩阵，μ为常数。因为可观测数据与潜数据之间是线性关系，所以这也是一个线性高斯模型。PPCA的核心问题是要求P(z|x)的大小。分三步：① 求x|z的分布；② 求x的分布；③ 求z|x的分布。下面是PPCA的概率图模型（不懂没关系，因为我也不懂）：

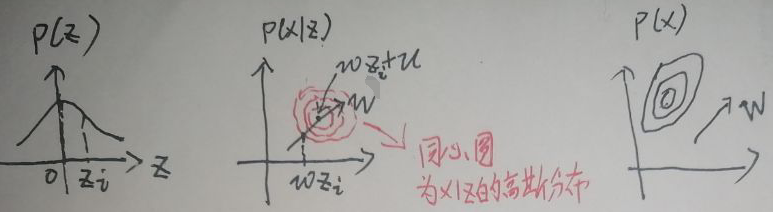
5.1 求x|z的分布

此时视z为常数，z～N(0,Ⅰ_q)，ε～N(0,δ²·Ⅰ_p)，所以期望E(x|z)=E(w·z+μ+ε)=w·z+μ+E(ε)=w·z+μ+0=w·z+μ；方差Var(x|z)=Var(w·z+μ+ε)=Var(ε)=δ²·Ⅰ_p。

因此x|z的分布为x|z～N(E(x|z),Var(x|z))=N(w·z+μ,δ²·Ⅰ_p)。

5.2 求x的分布

此时视z为变量，期望E(x)=E(w·z+μ+ε)=w·E(z)+μ+E(ε)=μ；方差Var(x)=Var(w·z+μ+ε)=wVar(z)w^T+Var(ε)=wⅠ_qw^T+δ²·Ⅰ_p=ww^T+δ²·Ⅰ_p。

因此x的分布为x～N(E(x),Var(x))=N(μ,ww^T+δ²·Ⅰ_p)。

5.3 求z|x的分布

使用可观测数据x与潜数据z去构造(x,z)^T，则(x,z)^T的分布为：

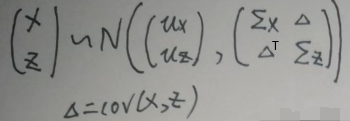
其中μ_x=μ，μ_z=0，Σ_x=ww^T+δ²·Ⅰ_p，Σ_x=Ⅰ_q，现在求Δ=cov(x,z)：

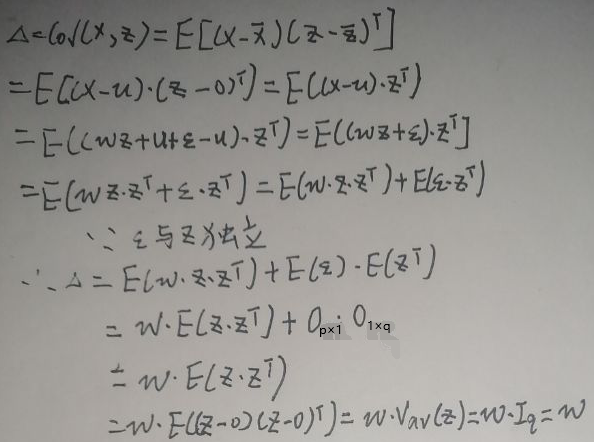
综上所述，构造的(x,z)^T的分布为：

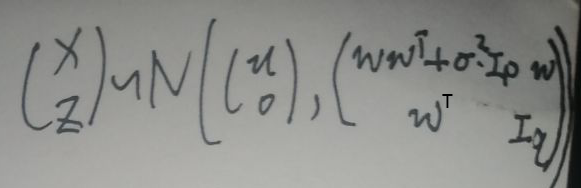
之后会用到机器学习-白板推导-系列（二）笔记：高斯分布与概率中【5 边缘概率与条件概率的求解】一整节的内容，疑惑的时候先去看相关内容。

首先将x看作上面提到的博客那一节的x_a，将z看作x_b，根据最后一张图片的倒数第二行便可以求出z|x的分布，这里就不详细展开了。

---

END