机器学习-白板推导系列笔记（二十六）-sigmoid信念网络

此文章主要是结合哔站shuhuai008大佬的白板推导视频：sigmoid信念网络_92min

全部笔记的汇总贴：机器学习-白板推导系列笔记

对应花书19.5、20.10

一、背景介绍

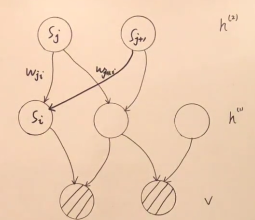
sigmoid信念网络是一种具有特定条件概率分布的有向图模型的简单形式。一般我们将sigmoid信念网络视为具有二值向量的状态$s$，其中状态的每个元素都受其祖先的影响。

s = { s 1 , s 2 , ⋯   , s T } = { v , h } = { v , h ( 1 ) , h ( 2 ) } σ ( x ) = 1 1 + exp ⁡ ( − x ) s=\{s_1,s_2,\cdots,s_T\}=\{v,h\}=\{v,h^{(1)},h^{(2)}\}\\\sigma(x)=\frac1{1+\exp(-x)} s={ s1​,s2​,⋯,sT​}={ v,h}={ v,h(1),h(2)}σ(x)=1+exp(−x)1​$$\begin{gathered} 1-\sigma (x)=\frac{1+\exp (-x)}{1+\exp (-x)}-\frac{1}{1+\exp (-x)} \\ =\frac{\exp (-x)}{1+\exp (-x)}=\frac{1}{1+\exp (x)}=\sigma (-x) \end{gathered}$$
$$\begin{gathered} P(s_i=1|s_{j:j<i})=\sigma (\sum _{j<i}{w}_{ji\cdot s_j}) \\ P(s_i=0|s_{j:j<i})=1-\sigma (\sum _{j<i}{w}_{ji\cdot s_j}) \\ =\sigma (-\sum _{j<i}{w}_{ji\cdot s_j}) \end{gathered}$$
$$\begin{gathered} P(s_i|s_{j:j<i})=\sigma (s_i^{\ast }\sum _{j<i}{w}_{ji}\cdot s_j) \\ {s}_i^{\ast }=2s_i-1 \end{gathered}$$

二、Gradient of log-likelihood

这里为了推导方便，我们没有考虑偏执$b$。

$$P(s)=\prod _{i}P(s_i|s_{j:j<i})=P(v,h)$$

log-likelihood：

$$\sum _{v\in V}logP(v)$$
$$\begin{gathered} \frac{\partial }{\partial w_{ij}}\log P(v)=\frac{1}{P(v)}\frac{\partial }{\partial w_{ij}}P(v) \\ =\frac{1}{P(v)}\frac{\partial {\sum }_{h}P(v,h)}{\partial w_{ij}} \\ =\sum _h\frac{1}{P(v)}\frac{\partial P(v,h)}{\partial w_{ij}} \\ =\sum _h\frac{P(h|v)}{P(h,v)}\frac{\partial P(v,h)}{\partial w_{ij}} \\ =\sum _{h}P(h|v)\frac{1}{P(s)}\frac{\partial P(s)}{\partial w_{ij}} \end{gathered}$$
$$\begin{gathered} \frac{1}{P(s)}\frac{\partial P(s)}{\partial w_{ij}}=\frac{1}{{\prod }_{k}P(s_k|s_{j:j<k})}\frac{{\prod }_{k\ne i}P(s_k|s_{j:j<k})\partial P(s_i|s_{j:j<i})}{\partial w_{ij}} \\ =\frac{1}{P(s_i|s_{j:j<i})}\frac{\partial P(s_i|s_{j:j<i})}{\partial w_{ij}} \\ =\frac{1}{P(s_i|s_{j:j<i})}\frac{\partial \sigma (s_i^{\ast }{\sum }_{j<i}{w}_{ji}\cdot s_j)}{\partial w_{ij}} \\ =\frac{1}{\sigma (s_i^{\ast }{\sum }_{j<i}{w}_{ji}\cdot s_j)}\cdot \sigma (s_i^{\ast }\sum _{j<i}{w}_{ji}\cdot s_j)\cdot \sigma (-s_i^{\ast }\sum _{j<i}{w}_{ji}\cdot s_j)s_i^{\ast }\cdot s_j \\ =\sigma (-s_i^{\ast }\sum _{j<i}{w}_{ji}\cdot s_j)s_i^{\ast }\cdot s_j \end{gathered}$$

所以，

$$\begin{gathered} \frac{\partial }{\partial w_{ij}}\sum _{v\in V}\log P(v)=\sum _{v\in V}\sum _{h}P(h|v)\sigma (-s_i^{\ast }\sum _{j<i}{w}_{ji}\cdot s_j)s_i^{\ast }\cdot s_j \\ =\sum _{v\in V}\sum _{h}P(h,v|v)\sigma (-s_i^{\ast }\sum _{j<i}{w}_{ji}\cdot s_j)s_i^{\ast }\cdot s_j \\ =\sum _{v\in V}\sum _{h}P(s|v)\sigma (-s_i^{\ast }\sum _{j<i}{w}_{ji}\cdot s_j)s_i^{\ast }\cdot s_j \\ =E_{(v,h)\sim P(s|v),v\sim P_{data}}[\sigma (-s_i^{\ast }\sum _{k<i}{w}_{ki}\cdot s_j)s_i^{\ast }\cdot s_j] \end{gathered}$$

精确推断无法求解，所以我们需要进行近似推断，这里需要用到的算法是醒眠算法（花书P398-19.5）。

三、醒眠算法

（一）介绍

学成近似推断是把推断视作一个函数。显式地通过迭代方法（不动点方程、基于梯度的优化）来进行优化通常代价高耗时巨大，我们通过学成一个近似推断来避免这种代价。将优化过程视作将一个输入$v$投影到一个近似分布$q^{\ast }=\underset{q}{\mathrm{argmax}}\Gamma (v,q)$的一个$f$的函数。一旦我们将多步的迭代优化过程看作函数，就可以用一个近似函数为$\hat{f}(v;\theta )$的神经网络来近似它。

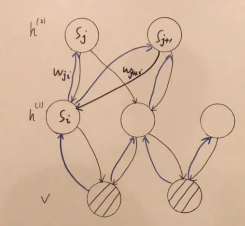
我们将正向的$W$称为Generative Connection，将反向的$W$用$R$来表示，称为Recognition Connection。

醒眠算法属于学成近似推断，是一个迭代算法，每一步分为两个阶段，第一个阶段称为Wake Phase，第二个阶段称为Sleep Phase。醒眠算法并非一个严谨的算法，他是一个启发式算法，是通过引入一个Recognition Connection来近似后验分布。

Wake Phase：

1. Bottom-up 从可见变量$v$出发，激活neuron（获得各层样本）
2. Learning Generative Connection（求$W$）

Sleep Phase：

1. Top-down 从最顶层出发，激活neuron（获得各层样本）
2. Learning Recognition Connection（求$R$）

（二）KL-Divergence

Generative model:$$p_{\theta }(v,h)(\theta =w)$$
Recognition Generative model:$$q_{\varphi }(h|v)\varphi =R$$

$$\log p(v)=ELBO+KL(q||p)$$$$\begin{gathered} ELBO=L=E_{q(h|v)}\left[\log \frac{p(v,h)}{q(h|v)}\right] \\ =E_{q(h|v)}[\log p(v,h)]+H[q] \end{gathered}$$

Wake Phase：（类似于EM算法中的M步）

$$E_{q_{\varphi }(h|v)}[\log p_{\theta }(v,h)]\approx \frac{1}{N}\sum _{i=1}^N\log p_{\theta }(v,h_i)$$
$$\begin{gathered} \hat{\theta }=\underset{\theta }{\mathrm{argmax}}{E}_{q_{\varphi }(h|v)}[\log p_{\theta }(v,h)],with\varphi fixed \\ =\underset{\theta }{\mathrm{argmax}}L(\theta ) \end{gathered}$$

Sleep Phase：（类似于EM算法中的E步）

$$\begin{gathered} \hat{\varphi }=\underset{\varphi }{\mathrm{argmax}}{E}_{p_{\theta }(v,h)}[\log q_{\varphi }(h|v)] \\ =\underset{\varphi }{\mathrm{argmax}}\int p_{\theta }(v,h)\log q_{\varphi }(h|v)dh \\ =\underset{\varphi }{\mathrm{argmax}}\int p_{\theta }(v)p_{\theta }(h|v)\log q_{\varphi }(h|v)dh \\ =\underset{\varphi }{\mathrm{argmax}}\int p_{\theta }(h|v)\log q_{\varphi }(h|v)dh \\ =\underset{\varphi }{\mathrm{argmax}}\int p_{\theta }(h|v)\log (\frac{q_{\varphi }(h|v)dh}{p_{\theta }(h|v)}\cdot p_{\theta }(h|v))dh \\ =\underset{\varphi }{\mathrm{argmax}}\int (p_{\theta }(h|v)\log \frac{q_{\varphi }(h|v)dh}{p_{\theta }(h|v)}+p_{\theta }(h|v)\log p_{\theta }(h|v))dh \\ =\underset{\varphi }{\mathrm{argmax}}\int p_{\theta }(h|v)\log \frac{q_{\varphi }(h|v)dh}{p_{\theta }(h|v)}dh \\ =\underset{\varphi }{\mathrm{argmax}}-KL(p_{\theta }(h|v)||q_{\varphi }(h|v)) \\ =\underset{\varphi }{\mathrm{argmin}}KL(p_{\theta }(h|v)||q_{\varphi }(h|v)) \end{gathered}$$

可以看出得到的KL表达式与Wake Phase所对应的KL并不相同，一个$q$在前$p$在后，另一个则恰好相反。原因是Sleep Phase中采用的样本并不是训练样本，而是全部都是抽样得到的生成样本。

下一章传送门：白板推导系列笔记（二十七）-深度信念网络