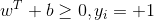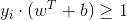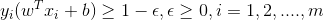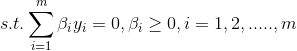svm(support vector machine)是一种二分类算法,它的目标在于寻找一个能将两种点分离的直线或平面或超平面。
如图(来自wiki):

图中的红线将两边数据点分开,这条线就是分割直线,同样的,在三维坐标轴中,将两边数据点分开的平面,称为分割平面;更高维的空间坐标轴,统称为分割超平面。
对于svm来说,找到这个分割超平面的准则或者是思路:使离分割平面较近的点(这种点被称为支持向量),尽可能的原理这个分割平面。
(再简单一些理解,就是如图中的虚线。虚线是穿过较近的一个点,以分割直线为平行线的一条直线。这个虚线距离分割直线的距离越大,效果越好。)
一、SVM的优化目标
既然 支持向量到分割平面的距离越大,模型效果越好,那么我们就可以将这个距离作为优化目标。
假设分割直线为: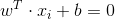
支持向量到分割平面的距离为: 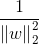
同时,我们还要满足一个条件,那就是样本如何判定正负(也就是如何分为两类)。假设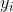
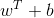
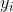
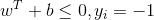
将条件加入优化目标,最终可以优化目标为一个带不等式约束的求最优值问题:
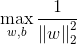
当然,可以将max转化为min,这样就和以前的求最小值看起来很类似的:
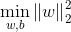
二、KKT条件
如上 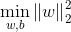
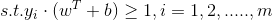
首先引入一个概念,上面这个公式首先是一个二次项的,其次,它带有一个不等式形式的约束条件。
对于这种带有不等式约束的优化问题,我们可以使用KKT条件转化。
KKT条件转化是拉格朗日乘子法在不等式约束上的扩展(这里不再展开叙述),其作用是能够将不等式约束以一种形式融合到优化目标的公式中,使其成为一个完整的公式。
那么我们的优化目标就能转化为:
![L(w,b,\beta ) = \frac{1}{2}\left \| w \right \|^2_2+\sum^m_{i=1}[1-y_i(w^T+b)],\beta _i\geq 0](https://img-blog.csdnimg.cn/20181224131158266)
三、优化目标求解
附上,从最初的优化目标到最终最简函数。(这一步并不能得到最终解,因为目前有三类变量需要确定,这一步最终使得三类变量化为一类。)


四、软间隔SVM
之前描述的svm对错误的训练样本完全没有容忍程度,但是现实中的数据集很少有完全干净的,那么为了让svm对错误的样本有一个容忍能力,提高svm泛化能力,我们引入一个参数ε,这样的svm称为软间隔SVM,之前的称为硬间隔SVM。
在图像坐标中表现为:
(ε越大,容忍能力越强)
最初的优化目标改写成: 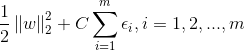
按照之前的推导过程,最后可以得到:
到此,也就得到了一个只关于β的损失函数,怎么求解,在第六部分的SMO讲解。
五、非线性SVM
之前讨论的无论是软间隔还是硬间隔的SVM,都只是在线性可分的角度去考虑,那么如果是一个线性不可分的问题呢?如下图(图来自wiki):

直线无法分割,需要这样的曲线才能分开。但是在svm中我们不去找这样的曲线,而是将目标投向高维空间。
低维空间线性不可分的数据,在更高维的某一空间,可能会转化为线性可分的数据。
那么如何将数据映射到高维空间?
很简单,比如原来是一个二维数据,拥有数据特征x1,x2,借助线性回归中学习的多项式扩展可以将其转化为(x1,x2,x1x2,x1的平方,x2的平方)这样的五维数据,svm就是采用这样的方式,但是直接去多项式扩展有个致命的问题:
当原始数据的维数本就很大,而且多项式扩展的次数还很高的时候,其计算使用的资源是指数级上升的。必须想一种办法能够得到一样的效果,还可以不用那么大的计算量。
于是核函数就出现了。
核函数(kernel function)
将样本x和z经过一个k(x,z)的映射,能够计算出和(x,z,xz,x的平方,z的平方,x的三次方……)一样的结果,我们就称这个k(x,z)为核函数。
常见的核函数有:
线性核函数虽然叫做核函数,但是和原先没有区别……
多项式核函数就是多项式展开了,可以看到里面的参数d就代表了多项式的次数(是次数,不是展开的维数)。
而高斯核函数才是真正的最优的,可以模拟高维空间,而且计算量并不大的核函数。为什么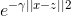
证明结果如下:

六、SMO(Sequencial Minimal Optimization)
上述得到的优化结果为:
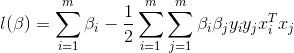
只剩下了一类需要求解的变量β,但是β并不是一个,而是每个样本对应一个βi,这样常规的计算又很麻烦了。
没关系,大佬提出了SMO算法,专门解决这个问题。
SMO算法基本思想:先确定其中的两个参数βi(确定方法为寻找违反KKT条件最大的βi),只更新这两个,别的不管。更新完成后,再来找一对βi进行更新,如此迭代,直到所有的βi都符合条件。
小问题1:为什么每次迭代更新两个参数?一个可以吗?
答:不可以,因为有如下约束条件,只改变一个βi会导致约束等式不成立:

小问题2:每一次更新,按照什么准则选择两个参数βi?
答:更新两个是因为不得已必须更新两个。那么第一个要选择的βi自然是我们最想解决的那个,也就是违反我们目标条件最大的那个。目标条件由推导过程得到,是βi与yig*(x)i的关系,如下:

SMO笔记