转载自:https://blog.csdn.net/whereisherofrom/article/details/79631703
Burnside引理
笔者第一次看到Burnside引理那个公式的时候一头雾水,找了本组合数学的书一看,全是概念。后来慢慢从Polya定理开始,做了一些题总算理解了。本文将从最简单的例子出发,解释Burnside引理和Polya定理。然后提供一些自己做过的和上述定理相关的题目和解题报告。
Burnside引理是为了解决m种颜色给n个对象染色的计数问题。
【例题1】如图1所示,2×2方格中每个格子可以选择染上2种颜色(红色或白色)。那么总共是2^4=16种情况。现在要问,如果旋转0度、90度、180度、270度后状态不变的方案算成同一种方案,问总共有多少种不同的方案。
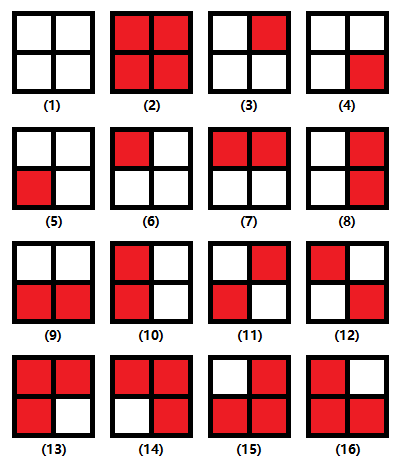
图1
将每种旋转认为是一种"置换",定义为gi,则上述问题总共有4种置换,分别描述为:

图2
用D(gi)表示在gi这种"置换"的作用下没有改变状态的方案集合,则根据图2易得:

图3
用|D(gi)|代表集合D(gi)中元素的个数,则有Burnside引理表示如图4所示:
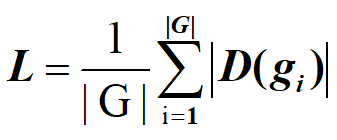
图4
L代表m种颜色给n个对象染色的总方案数,|G|代表置换个数,|D(gi)|代表在gi这种置换作用下没有改变状态的方案个数。
上文中的例子套用Burnside引理就是 L = (16+2+4+2)/4 = 6。
这道题几乎是所有解释Burnside引理的文章都会提到的一个例子,因为它看起来很直观,然而当染色数或对象数逐渐增多时,方案数呈指数级增长,再来举个例子。
【例题2】一个3×3的方格,用10种颜色给每个格子染色,旋转0度、90度、180度、270度后相同的算成相同,问总共有多少种方案。

图5
给每个格子编个号,每个格子有10种颜色,总共9个格子,总情况数10^9,已经没办法枚举出来了。继续从Burnside引理的定义出发,|D(gi)|代表在gi这种置换作用下没有改变状态的方案个数,置换总共四种,那么我们将这四种置换都列出来:
1)旋转0度:也就是我们将这个3×3的方格旋转0度后,有多少种方案是没有改变状态的,答案很显然,就是10^9。也就是说,无论你哪个格子染成什么颜色都没关系,旋转0度前后状态不变(这是显然的)。
2)旋转90度:①③⑦⑨循环变换、②④⑥⑧循环变换,⑤永远不变。表示成置换群的乘积就是(1379)(2468)(5)。那么我们发现,只要在同一个循环中的格子颜色一致,则在这种置换下状态永远不会改变。所以(1379)可以取10种颜色、(2468)可以取10种颜色、(5)可以取10种颜色,总方案数10^3。
3)旋转180度:置换群为(19)(28)(37)(46)(5),总方案数10^5。
4)旋转270度:类似旋转90度的,方案数10^3。
所以根据Burnside引理,总方案数就是(10^9 + 10^3 + 10^5 + 10^3)/4。
根据这个例子,就可以很好的理解Polya定理了。
Polya定理
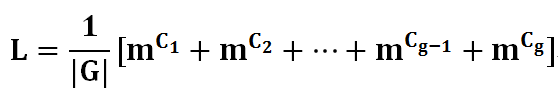
图6
m种颜色给n个对象染色的方案数如图所示。G代表变换(置换)的种类,其中Ci代表每种置换下的循环节。