快乐地打牢基础（12）——Burnside引理和 Polya计数公式

前置知识

1.群的定义

给定一个集合 $G = \{a,,b,c,...\}$ 和集合 $G$ 上的二元运算 $"*"$ ，并满足以下四个条件：

封闭性： $\forall a,b\in G,\exists c \in G,a*b=c$ 。
结合律： $\forall a,b,c\in G,(a*b)*c=a*(b*c)$ 。
单位元： $\exists \ e\in G,\forall a \in G a*e=e* a = a$ 。
逆元： $\forall a\in G,\exists b \in G,a*b=b*a=e,记\ b=a^{-1}$ 。

则称 $G$ 在运算 $“*”$ 下十一个群，简称 $G$ 是一个群，一般 $a*b$ 简写为 $ab$ .。 $“*”$ 可以是任何运算，如果 $“*”$ 是 $“+”$ ，就称为加法群，是 $“\times”$ ，就称为乘法群。如果群 $G$ 中的元素是有限的，就称为有限群，否则称为无限群，有限群中的元素个数称为有限群的阶。

2.群的运算

对于 $g\in G$ ，对于 $G$ 的子集 $H$ ，定义 $g*H=\{gh|g\in H\}$ ，简写为 $gH;H*g=\{hg|h \in H\}$ ,简写为 $Hg$ 。

对于 $G$ 的子集 $A,B$ ，定义 $A*B=\{ab|a\in A,b\in B\}$ ，简写为 $AB$ 。
对于 $G$ 的子集 $H$ ，记 $H^{-1}=\{h^{-1}|h\in H\}$
定理1：若 $(G,*)$ 是群，则对于任一 $g\in G,gG= Gg=G$ 。
定理2：若 $(G,*)$ 是群， $H$ 是 $G$ 的非空子集，并且 $(H,*)$ 也是群，那么称 $H$ 为 $G$ 的子群。

根据定理2 可以判断子集是否为一个子群： $HH=H,且H^{-1}=H$ 等价于 $H$ 是 $G$ 的子群。

3.置换

$n$ 个元素 $1,2,...n$ 之间的一个置换
$\left( \begin{matrix} 1 & 2 & ...&n \\ a_1 & a_2 &...& a_n \end{matrix} \right)$
表示 $1$ 被 $1$ 到 $n$ 中的某个数 $a_1$ 取代， $2$ 被 $1$ 到 $n$ 中的某个数 $a_2$ 取代，…，直到 $n$ 被 $1$ 到 $n$ 中的某个数 $a_n$ 取代，且 $a_1,a_2,...,a_n$ 互不相同。

4.置换群

置换群的元素是置换，运算是置换的连接。例如：
$\left( \begin{matrix} 1 & 2 & 3 & 4 \\ 3 & 1 & 2 & 4 \end{matrix} \right) \left( \begin{matrix} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \end{matrix} \right)= \left( \begin{matrix} 1 & 2 & 3 & 4 \\ 3 & 1 & 2 & 4 \end{matrix} \right) \left( \begin{matrix} 3 & 1 & 2 & 4 \\ 2 & 4 & 3 & 1 \end{matrix} \right)= \left( \begin{matrix} 1 & 2 & 3 & 4 \\ 2 & 4 & 3 & 1 \end{matrix} \right)$
可以验证置换群满足群的 4 个条件。

下面举个题目的例子：

He‘s Circles（SGU294）

题意： 有一个长度为N的环，上面写着’X’和’E’，问本质不同的环有多少种。(N不超过200000)。
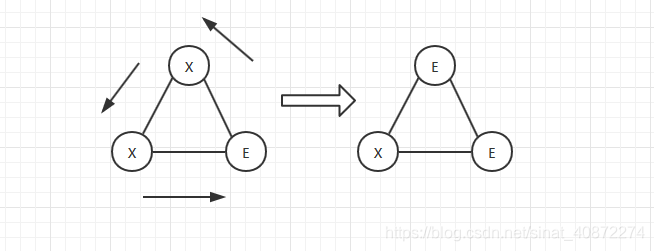
在这里插入图片描述
SGU已经挂掉了，所以不再用这题作为例题。

主要是用来练习找一下本题中的置换群 $G =$ {转0格，转1格，转2格,…,转n-1格}
转 0 格：
$\left( \begin{matrix} 1 & 2 & ...& n \\ 1 & 2 & ... & n \end{matrix} \right)$
转 1 格：
$\left( \begin{matrix} 1 & 2 & ...& n \\ 2 & 3 & ... & 1 \end{matrix} \right)$
转 2 格：
$\left( \begin{matrix} 1 & 2 & ...& n \\ 3 & 4 & ... & 2 \end{matrix} \right)$
$....$
转 n-1 格：
$\left( \begin{matrix} 1 & 2 & ...& n \\ n & 1 & ... & n-1 \end{matrix} \right)$

5.循环

先介绍一个循环的概念：
$\left( \begin{matrix} a_1 & a_2 & ... & a_n \\ \end{matrix} \right)= \left( \begin{matrix} a_1 & a_2 &... & a_n \\ a_2 & a_3 & a_n & a_1 \end{matrix} \right)$
称为 $n$ 阶循环。每个置换都可以写若干互不相交的循环的乘积，两个循环 $(a_1a_2...a_n)$ 和 $(b_1b_2...b_n)$ 互不相交是指 $a_i \not =b_j,i,j=1,2,...,n$ 。例如：
$\left( \begin{matrix} 1 & 2 &3 & 4&5 \\ 3 & 5 & 1 & 4&2 \end{matrix} \right)= (13)(25)(4)$
置换的循环节数是上述表示中循环的个数。例如 $(13)(25)(4)$ 的循环节数为 3。

BurnSide 引理

BurnSide 引理是群论中的一个重要结论，在组合数学中可用于计算等价类的个数，常用于Polya计数。

1.主要内容:

用 $D(a_j)$ 表示在置换 $a_j$ 下不变的元素的个数（不动点数）。 $L$ 表示本质不同的方案数（等价类的个数）， $|G|$ 是置换群中置换的个数。
$\displaystyle L = \frac{1}{|G|}\sum_{j = 1}D(a_j)$

对于上述 He‘s Circles（SGU294） 例子中 $N = 4$ 的情况，一共有4个置换：
$\left( \begin{matrix} 1 & 2 & 3 & 4 \\ 1 & 2 & 3 & 4 \end{matrix} \right) \left( \begin{matrix} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \end{matrix} \right) \left( \begin{matrix} 1 & 2 & 3 & 4 \\ 3 & 4 & 1 & 2 \end{matrix} \right) \left( \begin{matrix} 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \end{matrix} \right)$
因为每个点只有两个状态"X"和"E",所以一共有 $2^4=16$ 种情况。

所有方案在置换 $a_1$ 下都不变， $D(a_1) = 16$
XXXX 和 EEEE 在置换 $a_2$ 下不变， $D(a_2) = 2$
XXXX 和 EEEE 及 XEXE 和 EXEX 在置换 $a_3$ 下不变， $D(a_3) = 4$
XXXX 和 EEEE 在置换 $a_4$ 下不变， $D(a_4) = 2$

综上， $L = \frac{1}{4}(16 + 2 + 4 + 2)＝6$

下面主要介绍一个经典的案例：方阵着色问题
对于 $2*2$ 的方阵用黑白两种颜色涂色，问能得到多少种不同的图像？经过旋转使之吻合的两种方案，算是同一种方案。(图片来自百度百科)
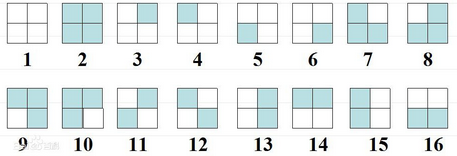
在这里插入图片描述
从图中我们可以发现案例3，案例4，案例5，案例6 可以通过旋转变为一种，我们就可以把（3,4,5,6）称为等价类（具体概念之后会有）。
那么一共有多少等价类呢？

1
2
3,4,5,6
7,8,9,10
11,12
13,14,15,16

所以我们可以知道等价类数目就是6，仔细想一想，我们可以发现这个例子就和我们上面 SGU例子中,N = 4 是一样的。

对于四个置换{逆时针旋转0°,逆时针旋转90°,逆时针旋转180°,逆时针旋转270°}，其不动点数分别为16, 2, 4, 2。所以等价类数目为(16+2+4+2)/4 = 6。

2.补充的两个概念

$E_k$ 等价类：设 $k$ 是 $1,2,...,n$ 中的某个元素， $k$ 在置换群 $G$ 作用下的轨迹上所有元素的集合

举个例子：

在方阵着色问题中，

方案 1 在{逆时针旋转0°,逆时针旋转90°,逆时针旋转180°,逆时针旋转270°}的四个置换下的都是方案1，所以 $E_1=\{1\}$
方案 3 ,在{逆时针旋转0°,逆时针旋转90°,逆时针旋转180°,逆时针旋转270°}的四个置换下分别是方案3,4,5,6所以 $E_3=\{3,4,5,6\}$ 。

$Z_k,k$ 不动置换类：** 设 $k$ 是 $1,2,...,n$ 中的某个元素，在置换群 $G$ 作用下使 $k$ 的位置保持不变的置换的全体。

举个例子：

对于上图的方案 11，{逆时针旋转0°,逆时针旋转90°,逆时针旋转180°,逆时针旋转270°}的四个置换下分别变成了方案11 ，方案12，方案11，方案12。所以只有第一个置换和第三个置换保证了位置不变
$Z_{11}=\{a_1,a_3\}$ 。

公式

总结一下：
BurnSide引理就是非等价着色数等于置换群中保持不变的着色的平均数，

等价类 = 各个置换下不动点个数的和 / 置换群中的置换个数。

Polya定理

Polay定理实际上是BurnSide引理的具体化，因为BurnSide中 $D(a_j)$ 并不是很好计算，搜索的话要大量的时间，所以Polya 定理提供了计算不动点的具体方法，达到快速求出 $D(a_j)$ 的目的。

假设一个置换有 $k$ 个循环，易知每个循环对应的所有位置颜色需一致，而任意两个循环之间选什么颜色互不影响。因此，如果有m种可选颜色，则该置换对应的不动点个数为 $m^k$ 。用其替换BurnSide引理中的 $D(a_j)$ ，得到等价类数目为：
　　
$L =\frac{1}{|G|}(m^{c(g_1)}+m^{c(g_2)}+...+m^{c(g_2)})$

$m^{c(g_i)}$ 为第 $i$ 个置换的循环个数。

总结一下：

Polya定理就是用（染色颜色^循环节数）求和来替代 Burnside中的不动点个数

各个置换下不动点个数的和 = 染色颜色^循环节数的和

所以我们解决求等价类个数的问题就转化成了两个主要问题：

构造置换群
计算置换群中每个置换的循环节数并求和。

下面是一道经典例题：
POJ 1286 Necklace of Beads

题意

给出三种颜色红绿蓝，对一串n个小球的环染色，环可以旋转和翻转，问最终可能有多少不同的染色方案。

思路

按照我们上面描述的那样，我们先解决第一个问题：构造我们的置换群。

分析题目，我们可以有 n个小球，3种颜色，我们可以通过旋转来找到本质相同的染色方案，但这样就结束了吗？并没有，我们来看下面这个例子：

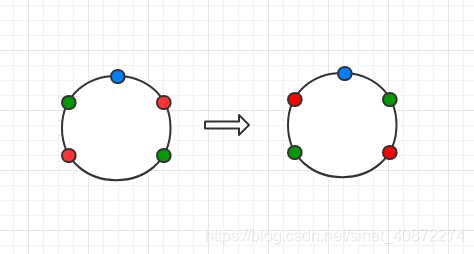
在这里插入图片描述
面对图中的情况，我们通过旋转是没有办法找到两个本质相同的方案，所以还需要考虑翻转的问题。

到此我们知道，可以把我们的置换主要分为两类：

旋转：旋转 $i$ 个小球的距离，那么会得到 $0～n-1$ 的置换方案，共有 $n$ 种。旋转 $i$ 个小球，我们的第 $j$ 个小球就转到了第 lab[j] 个位置。lab[j] = (i + j) % n + 1;
翻转：其实就是将对称的位置交换，第 j 个位置第 n + 1 - j 个位置交换。

解决了置换群的构造问题，那么下一步就是计算出循环节数的问题。
首先使用一种朴素的计算循环节数的方法，就是直接模拟我们手算循环节数的过程。

朴素循环节求法：

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <cmath>
#define ll long long 
using namespace std;

const int N = 30;
int lab[N];
bool vis[N] = {0};
int n;

//快速幂
ll qpow(ll a, ll b){
	ll res = 1;
	while(b){
		if(b & 1){
			res *= a;
		}
		a *= a;
		b >>= 1;
	}
	return res;
}
//计算循环节数
ll get_loop(){
	ll cnt = 0;
	memset(vis,0,sizeof(vis));
	for(int i = 1; i <= n; i++){
		if(vis[i]) continue;
		cnt++;
		int j = i;
		do{
			vis[j] = true;
			j = lab[j];	
		}while(!vis[j]);
	}
	return cnt;
} 
int main(){
	while(cin>>n){
		//printf("No smoking!");
		if(n == -1) break; 
		ll ans = 0;  
		if(n < 1){
			puts("0");
			continue;
		}
		for(int i = 0; i < n; i++){
			//旋转
			for(int j = 1; j <= n; j++) lab[j] = (i + j) % n + 1;
			ans += qpow(3,get_loop());
			//翻转
			for(int j = 1; j <= n / 2; j++) swap(lab[j],lab[n + 1 - j]);
			ans += qpow(3,get_loop());
		}
		printf("%lld\n",ans/(n*2));
	}
	return 0;
}

前人总结了一些关于循环节的一些结论：

①旋转。有n种置换，分别是1次旋转1个珠子，2个，3个…n个。对于1次旋转i个珠子，我们要求出循环节数可以先求出循环长度，一个位置置换x次之后回到原位，所以x=ny/i，要使x尽量小且为整数那么ny只能是lcm(n,i)，于是循环长度为lcm(n,i)/i，那么循环节数为总长除以循环长度，n/(lcm(n,i)/i)=gcd(n,i)【n*i/gcd(n,i)=lcm(n,i)】。所以1次旋转i个珠子的循环节数为gcd(n,i)。

②翻转。对于奇偶性分类讨论。

（1）n为奇数。对于每个点作为对称轴左右翻转，则共n个置换，循环节数(n+1)/2。

（2）n为偶数。

a.对于对称的两个点作为对称轴左右翻转。n/2个置换，循环节数(n+2)/2。

b.对于两个点中间的空格作为对称轴左右反转，n/2个置换，循环节数n/2。

则共n个置换。

所以不论奇偶总置换数为2n，答案为sum/2n。
.
———— 以上结论来自博客https://www.cnblogs.com/Sakits/p/6985058.html

下面给出一些简要证明：

①旋转

设当前的位置是 $p$ ，我们一次旋转 $x$ 个位置，假设我们旋转了 $k$ 次到了原位置。

那么我们就有
$p+kx\equiv p(mod \ n)$
两边同时减去 $p$ ，可以得到
$kx\equiv 0(mod \ n)$
可以知道 $n\ |\ kx$ ，又因为 $x\ |\ kx$ ，但是我们求的是循环节长度，即 $k$ 需要最小，又因为 $x$ 是常量，那么我们当然取 $n$ 和 $x$ 的最小公倍数了。
$kx = lcm(n,x)$
又因为 $\displaystyle lcm(n,x)=\frac{nx}{gcd(n,x)}$
可以得到 $\displaystyle kx = lcm(n,x)=\frac{nx}{gcd(n,x)}\\\ \\\\k = \frac{n}{gcd(n,x)}$
因为循环节的长度为 $\displaystyle \frac{n}{gcd(n,x)}$ ，又一共有 $n$ 个元素，且这 $n$ 个元素对称，那么显然循环节个数就是 $gcd(n,x)$ 。

②翻转

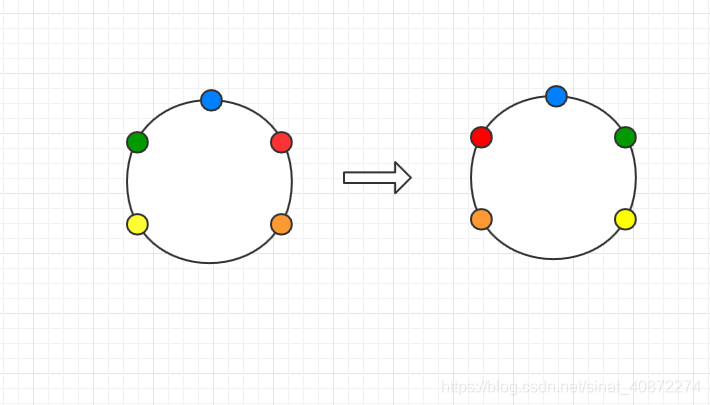
(1)奇数个点

奇数个点，对称轴肯定是经过某一个点，(下图的蓝点)，那么，每一对对称的点就形成了一个循环节。

以下图为例，蓝色点为对称的点，绿点和红点是一个循环节，黄色和橙色是一个循环节，蓝色是不动点本身是一个循环节。所以一共是 $\displaystyle\frac{n-1}{2}+1=\frac{n+1}{2}$ 个循环节。
在这里插入图片描述
(2)偶数个点
偶素有两种对称的可能

对称轴过其中两点
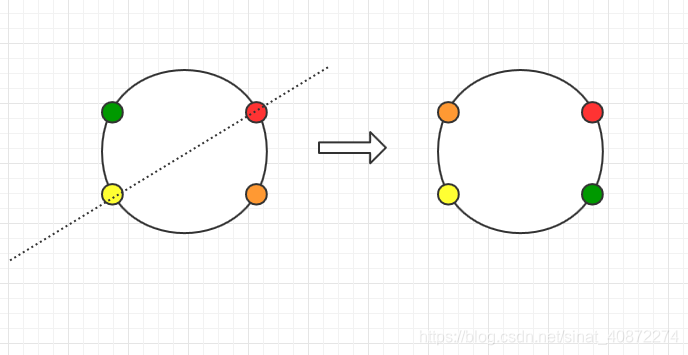有 $2$ 个不动点，剩下的 $n-2$ 每两个点成一个循环节，共 $\displaystyle\frac{n-2}{2}+2=\frac{n+2}{2}$ 个。
对称轴在两点间的空格
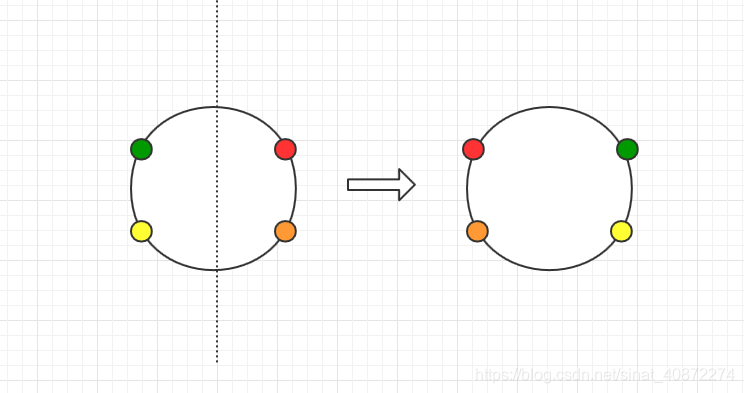每两个点成一个循环节，共 $\displaystyle\frac{n}{2}$ 个。

下面是运用结论求法

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <cmath>
#define ll long long 
using namespace std;

const int N = 30;
int lab[N];
bool vis[N] = {0};
int n;
//最大共约数
ll gcd(ll a, ll b){
	return b == 0 ? a : gcd(b,a % b);
} 

//快速幂 
ll qpow(ll a, ll b){
	ll res = 1;
	while(b){
		if(b & 1){
			res *= a;
		}
		a *= a;
		b >>= 1;
	}
	return res;
}
int main(){
	while(cin>>n){
		//printf("No smoking!");
		if(n == -1) break; 
		ll ans = 0;  
		if(n < 1){
			puts("0");
			continue;
		}
		//旋转置换 
		for(int i = 1; i <= n; i++)
			ans += qpow(3,gcd(i,n));
		//对称置换 
		if(n&1) {
            ans+=qpow(3,n/2+1)*n;
        } else {
            ans+=qpow(3,n/2+1)*(n/2);
            ans+=qpow(3,n/2)*(n/2);
        }
		printf("%lld\n",ans/(n*2));
	}
	return 0;
}

Miserable_ccf

发布了141 篇原创文章 · 获赞 71 · 访问量 6万+

私信关注