先来简单介绍一下置换运算:
置换就是把n个元素中某些元素换个顺序,形成排列。置换之间可以定义乘法运算,置换的乘法仍然是置换。比如a,b是两个置换,那么ab的含义就为先进行b置换,在进行a置换,一般资料上的运算顺序都是从右向左。
我们定义一个新的概念叫做置换群,它的所有成员都是置换,可以类比于集合。
置换群有一些性质,可以适当了解一下,如果不了解也没有关系。
(1)封闭性,对于置换群中的置换进行乘法运算,所得的结果仍然在置换群中。
(2)置换的乘法满足结合律,但并不满足交换律。
(3)单位元,存在一个置换,与其他任意置换做乘法运算不改变原来的置换。
(4)逆元,对于任意置换来说,存在一个置换,它们做乘法等于单位元。
读到这里,可能对于置换的运算还是比较陌生,那我们接下来看一个置换运算的例子:
从右向左运算,可以简单的得到结果。
为了处理方便,我们可以把置换分解成循环的乘积,比如 =(1 3)(2 5)(4),它的循环节是3。后面这个东西是什么意思呢,它代表我们把1换成3,3换成1;2换成5;5换成2。再一般些,比如(a b c),就代表a->b,b->c,c->a。不难发现,所有的置换都可以分解成若干个这样的循环节。
下面开始介绍置换的运用:
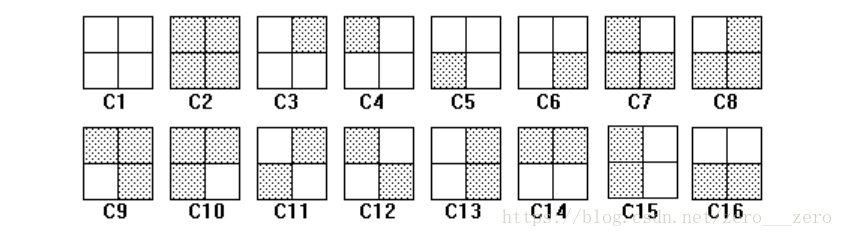
等价计数类问题:有这样一个经典问题,给一个2*2的方格中涂上黑白两色,规定如果一种涂色方案经过旋转得到另一种涂色方案,那么称这两种涂色方案是等价的,问一共有多少种不同的涂色方案?
原本应该是上面的16种方案,但是去掉等价的方案以后,得到的答案应该是6种。
如何解决这个问题。我们定义一个置换群G={逆时针旋转0°,逆时针旋转90°,逆时针旋转180°,逆时针旋转270°}。如果对于一个置换f来说,某一个着色方案s经过置换f以后不变,则称s是f的不动点。把f的不动点数目记作C(f),那么所求答案是所有C(f)的平均值,此结论称为Burnside定理,具体证明略。
例如在本题中,逆时针旋转0°有16个不动点(任何一个方案不旋转,都不会变),逆时针旋转90°和270°都只有C1,C2两个不动点,逆时针旋转180°有C1,C2,C11,C12这4个不动点,所以等价方案有(16+2+2+4)/4=6。
具体如何求C(f)呢,我们先把2*2的方格按照从上到下,从左到右的顺序编号成1,2,3,4。
比如对于逆时针旋转180°来说,就是对角线上的编号互换了,写成循环乘积形式就是(1 3)(2 4),所以这种置换必须是对角线的小方格颜色相同才会有不动点,着色方案就是2*2=4种。
一般的,如果置换f分解成m(f)个循环的乘积,那么每个循环节内格子的颜色必须相同,假设涂k种颜色,则C(f)=k^(m(f)),带入Burnside引理的表达式后得出Polya定理,等价类的个数等于所有置换f的k^(m(f))的平均数。