【背包问题】01 背包

一、题目描述

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。第 i 件物品的价值是 $v_i$，种类是 $w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。返回最大价值。

二、题解

方法一：暴力递归

问题中的参数个数就是我们解决该问题所要满足的约束条件，对于 01 背包，我们有两个约束条件，分别是：

• 从 n 个物品取；
• 物品的总容量不大于 m。

问题可抽象定义为 $F(n, m)$：表示考虑把 n 个物品放进容量为 m 的背包，使得价值最大。

public int knapsack01(int[] v, int[] w, int i, int C) {
  int n = v.length;
  return dfs(v, w, n-1, C);
}

private int dfs(int[] v, int[] w, int i, int C) {
  if (i < 0 || C <= 0)  return 0;
  //第一种策略：直接不选
  int res = dfs(v, w, i - 1, C);
  if (C >= w[i])
    res = Math.max(res, dfs(v, w, i - 1, C - w[i]));
  return res;
}

复杂度分析

• 时间复杂度： $O(2^n × m)$，
• 空间复杂度： $O(n)$，

是否可用贪心来做？优先放入平均价值 $\cfrac{v_i}{w_i}$ 最大的物品？答案是否定的，反例如下：

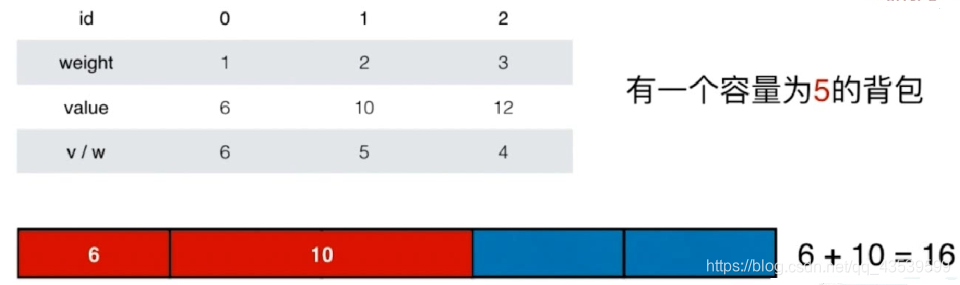
我们浪费了背包的两个容量，其实我们可以放入第 1 个物品( $v_1 = 10$) 和第 2 个物品( $v_2=12$) 使得背包价值最大 (22)，而不是 16。

---

方法二：记忆化搜索

当每次选择物品时，暴力递归的代码存在许多重复的计算。memo 数组就是把相同的计算结果存储起来，共后序选择物品时取。

private int dfswWithMemo(int[] v, int[] w, int i, int C) {
  if (i < 0 || C <= 0) return 0;
  if (memo[i][C] != 0) return memo[i][C];
  
  int res = dfswWithMemo(v, w, i-1, C);
  if (C >= w[i]) {
    res = Math.max(res, dfswWithMemo(v, w, i - 1, C - w[i]));
  }
  return res;
}
int[][] memo = null;
public int knapsack01(int[] v, int[] w, int i, int C) {
  memo = new int[i][C+1];
  int n = v.length;
  return dfswWithMemo(v, w, n-1, C);
}

复杂度分析

• 时间复杂度： $O(n × m)$，
• 空间复杂度： $O(n × m)$，

---

方法二：dp

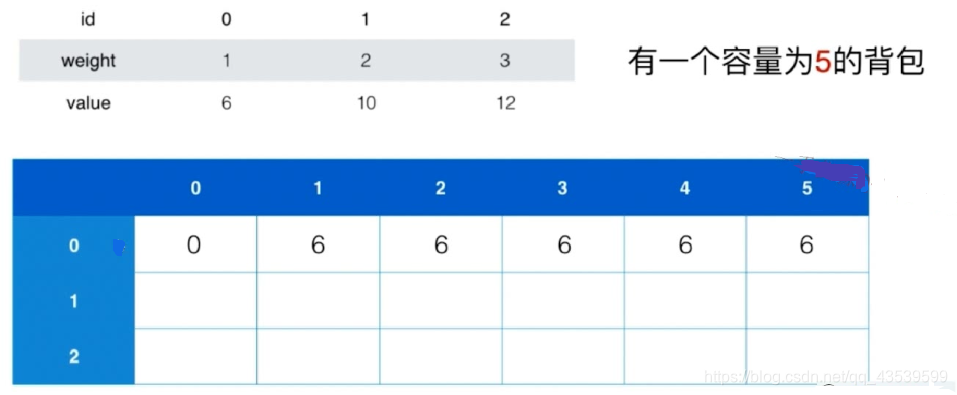
有容量为 5 的背包，当放入第 0 个物品时，我们一定会把第 0 个物品放进容量为 $>=1$ 时背包中：表示放入第 0 个物品所能获得的最大价值。

当再考虑放第 1 个物品时，意味着我们考虑第 0 和 第 1 个物品时，背包的最大价值的变化。所以，放入第 1 个物品是基于放入第 0 个物品后的结果得到临时最大价值，所以当重量为 0/1 时，我们还不能把第 1 个物品 $(w_i = 1)$放在重量状态为 1 时的背包，

当背包体积状态为 3 时，有两种选择：

• 放入第 0 和 1 号物品，dp[1][3] = dp[0][3-w[0]] + v[1] = 6 + 10 = 16
• 不放入 1 号物品时，dp[1][3] = dp[0][3] = 6；
  • 显然选择放入第 1 件物品会得到临时最大价值。

背包容量为 3 时，可第 2 件物品放入背包，放入后，背包剩余空间为 0，

• 但获得的价值是 10；
• 放入第 2 件物品可得原价值 16。
  

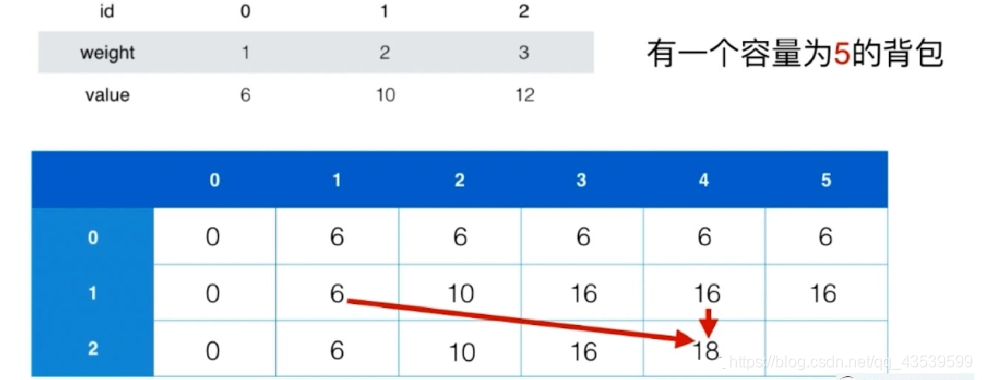
容量状态为 4 时的背包，可放入第 2 件物品，放入后，背包剩余空间为 1。

• 再放入第 1 件后，得到总价值为 18。
• 仅仅放入第 2 件物品得到的价值是 12.

最后，背包容量状态为 5，可放入第 2 件物品，放入后，背包容量剩余 2：

• 再把第 1 件物品放入背包，得到价值 22。
• 仅把第 2 件物品放入背包，进得到价值 12.

最后，我们总结出 01 背包的几点：

• 定义初始状态：dp[0][0...C] = j >= w[i] ? v[0] : 0，考虑第 0 号物品，尝试放入当重量状态为 [0…C] 时的背包。
• 定义状态方程 $f[i][j]$：表示所有选法集合中，只从前 i 个物品中选，并且总体积 $<=j$ 的选法的集合，它的值是这个集合中每一个选法的最大值。这个子结构有两种情况导致：
  • 当 $j<w[i]$，即前背包容量不够 ，此时的最优解为前 $i-1$ 个物品最优解。
    • $f[i][j] = f[i-1][j]$。
  • 当 $j>=w[i]$，当前背包容量够，比较选完的总价值与不选第 i 个物品时的总价值。
    • $f[i][j] = max(f[i-1][j-w[i]] + v[i]，f[i-1][j])$

/**
 * @param C 背包容积
 * @param V 各物品的价值
 * @param W 各物品的体积
 * @return
 */
public static int knapsack01(int C, int[] V, int[] W) {

  int n = V.length;
  if (n == 0) return 0;
  int[][] dp = new int[n][C + 1];

  for (int j = 0; j <= C; j++) {
    dp[0][j] = j >= W[j] ? V[j] : 0;  //只放入第0号物品
  }

  for (int i = 1; i < n; i++)
  for (int j = 0; j <= C; j++) {
    if (j < W[i])
      dp[i][j] = dp[i-1][j];
    else
      dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-W[i]] + V[i]);  //if可以去掉
  }
  return dp[n-1][C];
}

复杂度分析

• 时间复杂度： $O(n × C)$，n 是物品总数，C 为背包容积。
• 空间复杂度： $O(n × C)$，

附：空间压缩（一）

通过第一版代码分析，可发现第 i 行元素只依赖第 i-1 行，理论上只需保存 2 行状态。可将空间复杂度从 O(n × C) 降到 $O(2 × C) = O(C)$。

public static int knapsack01_1(int C, int[] V, int[] W) {
    
  int n = V.length;
  if (n == 0)  return 0;
  int[][] dp = new int[2][C + 1];
  
  for (int j = 0; j <= C; j++) {
    dp[0][j] = j > W[j] ? V[j] : 0;
  }

  for (int i = 1; i < n; i++)
  for (int j = 0; j <= C; j++) {
    if (j < W[j])
      dp[i%2][j] = dp[(i-1)%2][j]; 
    else 
      dp[i%2][j] = Math.max(dp[(i-1)%2][j-W[i]] + V[i], dp[(i-1)%2][j]);
  }
  return dp[(n-1)%2][C];
}

复杂度分析

• 时间复杂度： $O(n × C)$，
• 空间复杂度： $O(C)$，

---

附：空间压缩（二）

其实还可以使用逆向枚举背包容量代替模 2 运算。

先初始化第 0 行元素，即只考虑第 0 个物品时的最大价值。

然后，我们对每一个物品 i 逆向枚举背包重量 C。先考虑背包为 5 容量状态，可放入第 1 件物品，背包剩余空间为 3：

• 放入第 1 和 0 件物品，总价值为 16.
• 不放入第 1 件，总价值为 6.

当枚举容量为 4 时的背包，放入第 1 个物品，那么容量只剩 2，可再放入 0 号物品，此时背包总价值为 16.

依次类推，知道背包容量 j 不能放入第 i 号物品时（即，j < w[i]），枚举下一个物品。

public static int knapsack01_2(int C, int[] V, int[] W) {
    
  int n = V.length;
  if (n == 0) return 0;
  int[] dp = new int[C+1];

  for (int i = 0; i < n; i++) {
    dp[i] = i > W[i] ? V[i] : 0;
  }

  for (int i = 1; i < n; i++) {
    for (int j = C; j >= W[i]; j--)
      dp[j] = Math.max(dp[j - W[i]] + V[i], dp[j]);
  }
  return dp[C];
}