机器人学之运动学（一）：运动学描述基础

1.刚体运动状态描述

1. 平面

• 首先在平面上定义世界坐标系(world frame)，一个平面上有三个自由度来描述刚体，即2个移动自由度（沿x轴水平移动和沿y轴上下移动）和1个旋转自由度（沿刚体质心顺/逆时针转动）。

2. 空间

• 建立三维空间直角坐标系，一个空间内有6个自由度解释刚体的运动，即3个移动自由度（沿x,y,z轴移动）和3个转动自由度（沿x,y,z轴旋转）

3. 整合刚体的状态

• 在刚体上建立坐标系(body frame)，常建立在质心上
• 移动：由body frame的原始位置决定，即刚体质心相对世界坐标系原点的位置
• 转动：由body frame的姿态决定，即3个坐标轴相对世界坐标系的姿态

4. 刚体运动状态的描述

• 记录不同时间点刚体质心的轨迹，已知轨迹的位置，求得轨迹对时间的微分，就是质心的速度，再次微分，就是质心运动的加速度。
• 已知刚体转动的姿态，由微分和二次微分，可求得刚体转动的角速度和角加速度。
• 借由刚体在平面上的三个自由度和空间上的六个自由度的微分和二次微分，可以知道刚体的移动和转动状态。

2.移动

• 移动：以向量 $\vec P$描述建立在刚体上的坐标系{B}的原点相对世界坐标系{A}的状态。
• 将刚体质心相对于{A}的位置映射为向量，与世界坐标做连接。
• 假设质心P坐标可以表示为：
  $\vec P= \left[ \begin{matrix} P_x \\ P_y \\ P_z \end{matrix} \right] \tag{1}$
  $P_x,P_y,P_z$是P坐标在空间的三个分量，向量本身代替一个方向。
• 描述body frame的原点（相对于世界坐标）： $\vec P= \left[ \begin{matrix} P_x \\ P_y \\ P_z \end{matrix} \right] =^AP_B\tag{2}$
• 向量表达body frame上坐标轴的方向： $\vec X_B,\vec Y_B,\vec Z_B$

3.转动

• 转动：描述{B}相对{A}的姿态。
• 表达方式：旋转矩阵(功能一)如下，
  $^A_B R= \left[ \begin{matrix} | & | & | \\ P_x & P_y & P_z\\ | & | & | \end{matrix} \right] \tag{3}$
  其中， $^A_B R$表示B相对于A的状态，A为基准，矩阵的三行表示
  body frame的三个坐标轴所指向的方向。
• {B}在{A}上投影：
  $^A_B R= \left[ \begin{matrix} | & | & | \\ ^A\vec X_B &^A\vec Y_B &^A\vec Z_B\\ | & | & | \end{matrix} \right] = \left[ \begin{matrix} {\vec X_ B}{\vec X_A} &{\vec Y_B}{\vec X_A} & {\vec Z_B}{\vec X_A} \\ {\vec X_B}{\vec Y_A }&{\vec Y_B}{\vec Y_A} &{\vec Z_B}{\vec Y_A}\\ {\vec X_B}{\vec Z_A }&{\vec Y_B}{\vec Z_A} & {\vec Z_B}{\vec Z_A} \end{matrix} \right] \tag{4}$

4.选择矩阵

• 旋转矩阵特性一：
  $^A_B R= \left[ \begin{matrix} | & | & | \\ ^A\vec X_B &^A\vec Y_B &^A\vec Z_B\\ | & | & | \end{matrix} \right] = \left[ \begin{matrix} {\vec X_ B}{\vec X_A} &{\vec Y_B}{\vec X_A} & {\vec Z_B}{\vec X_A} \\ {\vec X_B}{\vec Y_A }&{\vec Y_B}{\vec Y_A} &{\vec Z_B}{\vec Y_A}\\ {\vec X_B}{\vec Z_A }&{\vec Y_B}{\vec Z_A} & {\vec Z_B}{\vec Z_A} \end{matrix} \right] \tag{4}$
  前后向量互换
  $=\left[ \begin{matrix} {\vec X_A} {\vec X_ B}&{\vec X_A}{\vec Y_B} & {{\vec X_A} \vec Z_B}\\ {\vec Y_A } {\vec X_B}&{\vec Y_A}{\vec Y_B} &{\vec Y_A}{\vec Z_B}\\ {\vec Z_A } {\vec X_B}&{\vec Z_A}{\vec Y_B} &{\vec Z_A} {\vec Z_B} \end{matrix} \right] = \left[ \begin{matrix} — & ^B\vec X_A^T & — \\ — &^B\vec Y_A ^T&—\\ — & ^B\vec Z_A^T & — \end{matrix} \right] \tag{5}$
  等价于
  $= \left[ \begin{matrix} | & | & | \\ ^B\vec X_A &^B\vec Y_A &^B\vec Z_A\\ | & | & | \end{matrix} \right] ^T =^B_A R^T \tag{6}$
  意思就是说，{B}对{A}的旋转矩阵与{A}对{B}的旋转矩阵是互为转置矩阵的关系。

  • 旋转矩阵特性二
    ${^A_B R^T}^A_B R= \left[ \begin{matrix} | & | & | \\ ^A\vec X_B &^A\vec Y_B &^A\vec Z_B\\ | & | & | \end{matrix} \right] ^T \left[ \begin{matrix} | & | & | \\ ^A\vec X_B &^A\vec Y_B &^A\vec Z_B\\ | & | & | \end{matrix} \right] \tag{7}$
    $= \left[ \begin{matrix} — & ^A\vec X_B^T & — \\ — &^A\vec Y_B ^T&—\\ — & ^A\vec Z_B^T & — \end{matrix} \right] \tag{8} \left[ \begin{matrix} | & | & | \\ ^A\vec X_B &^A\vec Y_B &^A\vec Z_B\\ | & | & | \end{matrix} \right]$
    $= \left[ \begin{matrix} 1 & 0 & 0 \\ 0 &1&0\\ 0 & 0 & 1 \end{matrix} \right] =I_3 \tag{9}$
    结果是3X3的单位矩阵。
    由此，可以推导出：
    $^A_B R^T=^A_B R^{-1}=^B_A R\tag{10}$

• 旋转矩阵：可用于转换向量坐标（功能二）

• 原始坐标： $^BP={^BP_x}{\vec X_B}+{^BP_y}{\vec Y_B}+{^BP_z}{\vec Z_B}$

• 新坐标： $^AP={^AP_x}{\vec X_A}+{^AP_y}{\vec Y_A}+{^AP_z}{\vec Z_A}$

• 坐标分量如下：
  $^AP_X={^BP}{\vec X_A}={\vec X_B}{\vec X_A}{^BP_x}+{\vec Y_B}{\vec X_A}{^BP_y}+{\vec Z_B}{\vec X_A}{^BP_z}$
  $^AP_y={^BP}{\vec Y_A}={\vec X_B}{\vec Y_A}{^BP_x}+{\vec Y_B}{\vec Y_A}{^BP_y}+{\vec Z_B}{\vec Y_A}{^BP_z}$
  $^AP_z={^BP}{\vec Z_A}={\vec X_B}{\vec Z_A}{^BP_x}+{\vec Y_B}{\vec Z_A}{^BP_y}+{\vec Z_B}{\vec Z_A}{^BP_z}$

• 表示成矩阵即为：
  $^AP= ^A \left[ \begin{matrix} P_x \\ P_y \\ P_z \end{matrix} \right] =\left[ \begin{matrix} {\vec X_ B}{\vec X_A} &{\vec Y_B}{\vec X_A} & {\vec Z_B}{\vec X_A} \\ {\vec X_B}{\vec Y_A }&{\vec Y_B}{\vec Y_A} &{\vec Z_B}{\vec Y_A}\\ {\vec X_B}{\vec Z_A }&{\vec Y_B}{\vec Z_A} & {\vec Z_B}{\vec Z_A} \end{matrix} \right] ^B \left[ \begin{matrix} P_x \\ P_y \\ P_z \end{matrix} \right] ={^A_BR}{^BP} \tag{11}$

  • 旋转矩阵：进一步描述问题转动的状态。
  • 以三个坐标轴为旋转轴，旋转角为 $\theta$。
    
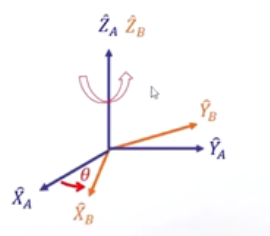
  • 以Z轴为旋转轴，旋转矩阵为：
    $R_{\vec Z_A}= \left[\begin{matrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta &0\\ 0& 0 & 1 \end{matrix} \right] \tag{12}$
  • 以X轴为旋转轴，旋转矩阵为：
    $R_{\vec X_A}= \left[\begin{matrix} 1 & 0 & 0 \\ 0 & cos\theta &-sin\theta\\ 0& sin\theta & cos\theta \end{matrix} \right] \tag{13}$
  • 以Y轴为旋转轴，旋转矩阵为：
    $R_{\vec Y_A}= \left[\begin{matrix} cos\theta & 0 & sin\theta \\ 0 & 1 &0\\ -sin\theta& 0 & cos\theta \end{matrix} \right] \tag{14}$

• 本质上就是旋转后的坐标轴在原坐标轴上的投影向量。