机器人学笔记(2)正运动学

机器人学笔记(2)正运动学

改进DH描述(MDH)

一般而言，机器人均采用仅有一个自由度的连杆，在极少数情况下，会采用自由度为n的连杆，在此时，可以将之视为n个自由度为1，长度为0的连杆相连接而成，所以以下针对自由度为1的连杆的讨论可以在不失一般性的前提下完成。

首先从操作臂的基座开始，将其命名为连杆0，第一个可动连杆为连杆1，最后一个可动连杆为连杆n。为了使末端执行器顺利到达位置，机械臂一般需要最少6个关节（这是显然的，因为空间中的一个位置描述需要六个参数）。

那么，如何确定一个连杆的运动情况呢？答：只需要确定连接该连杆的两个关节轴的相对位置关系就可以了！如图：

在三维空间之中，最一般的情况下，可以将两个轴视作两条异面直线，在空间中，确认两条异面直线之间的关系只需要两个参数（可以参考在平面中，确定两条直线之间的关系仅需要知道它们之间的夹角）。

但如果有多个连杆的话，仅仅知道每个轴的位置关系是不够的，还需要知道连杆之间的相对位置关系，我们定义两相邻连杆公共轴线方向间的距离为连杆偏距，连杆偏距为$d_i$，用另一个参数表示连杆沿公共轴线的夹角，为${\theta }_i$，如下图。

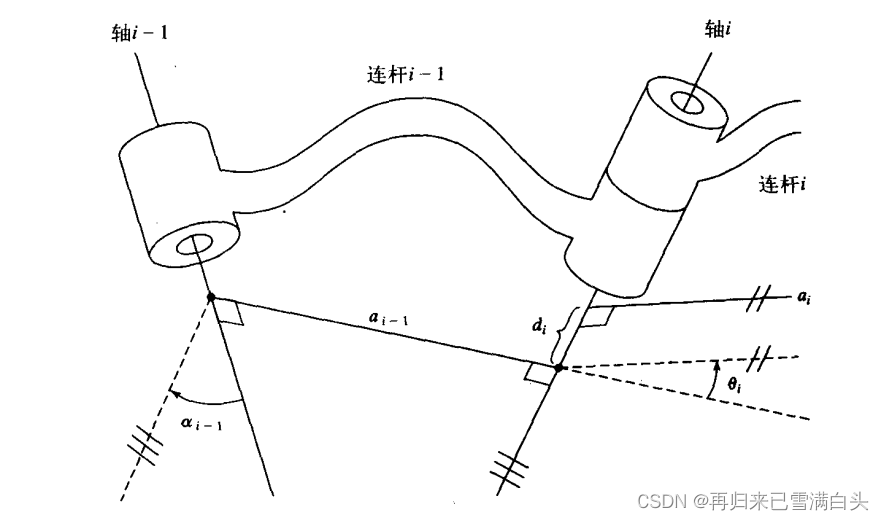
当然，对于初始连杆和末端连杆这样的特殊情况，如果关节1为转动关节，则${\theta }_1$的零位可以任取，并且此时$d_1=0$，如果关节1是移动关节，$d_1$的零位可以任取，而${\theta }_1=0$，这样的设置和关节n相同。

连杆附加坐标系的建立

为了描述连杆间相对的位置关系，需要在每个连杆上固定坐标系，我们将固连在连杆i上的坐标系称为坐标系i。

对于中间连杆，将坐标系i的$Z$轴称为$Z_i$，并且$Z_i$轴与轴线$i$方向重合。原点位于轴线$i$和中垂线的交点处，$X_i$沿$a_i$方向有关节i指向关节i+1。

当$a_i=0$时，$X_i$垂直于$Z_i$和$Z_{i+1}$所在的平面。按右手定则绕$X_i$轴的转角为${\alpha }_i$，由于$X_i$轴的取向有两轴，所以转角${\alpha }_i$的符号也可以去两种。

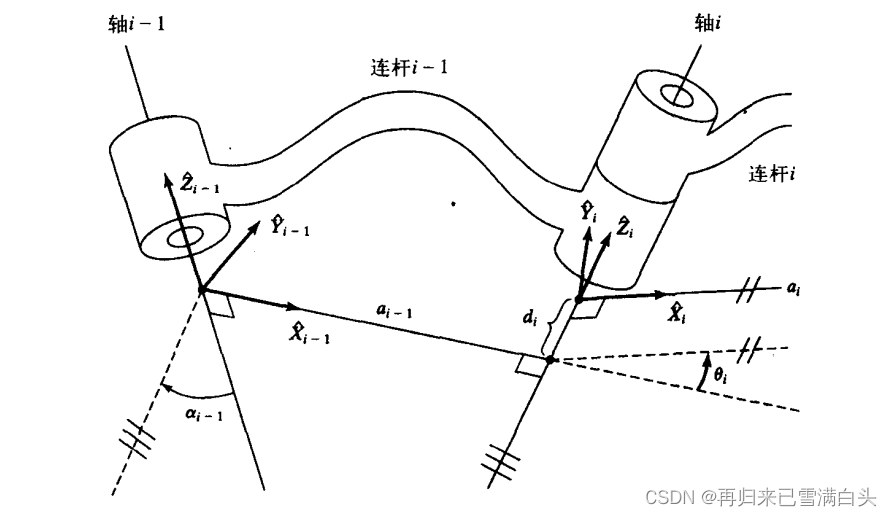
固连于机械臂基座上的坐标系为坐标系0，这个坐标系一般而言是不动的，一般可以把这个当成基座来研究，被称为参考坐标系。参考坐标系的坐标轴可以任意设定，通常将轴1的方向(只有连杆0，没有轴0)设为$\widehat{Z_0}$，当关节变量1为0时，坐标系0与坐标系1相重合，按照这个规定的话，则恒有：$a_0=0,{\alpha }_0=0$，当关节1为移动关节时，有${\theta }_0=0$，当关节1为转动关节时，有$d_0=0$。

对于转动关节n(即最后一个link)，设定${\theta }_n=0$。此时$\widehat{X_N}$轴与$\widehat{X_{N-1}}$轴方向一致，原点设置使得$d_n=0$，对于移动关节n，设定$\widehat{X_N}$轴方向使之与$\widehat{X_{N-1}}$轴方向一致。

这样设定坐标系的好处是：

操作臂正运动学

接下来，我们想要建立从连杆0到连杆n位置的推导，对于任意机器人系统来说，上述4个参数只有一个是变量，另外三个参数是由机械系统所决定的。通过为每一个连杆建立坐标系，我们将整个问题分解为n个子问题，即${}_i^{i-1}T$，首先，我们为连杆定义三个中间坐标系：P,Q,R。

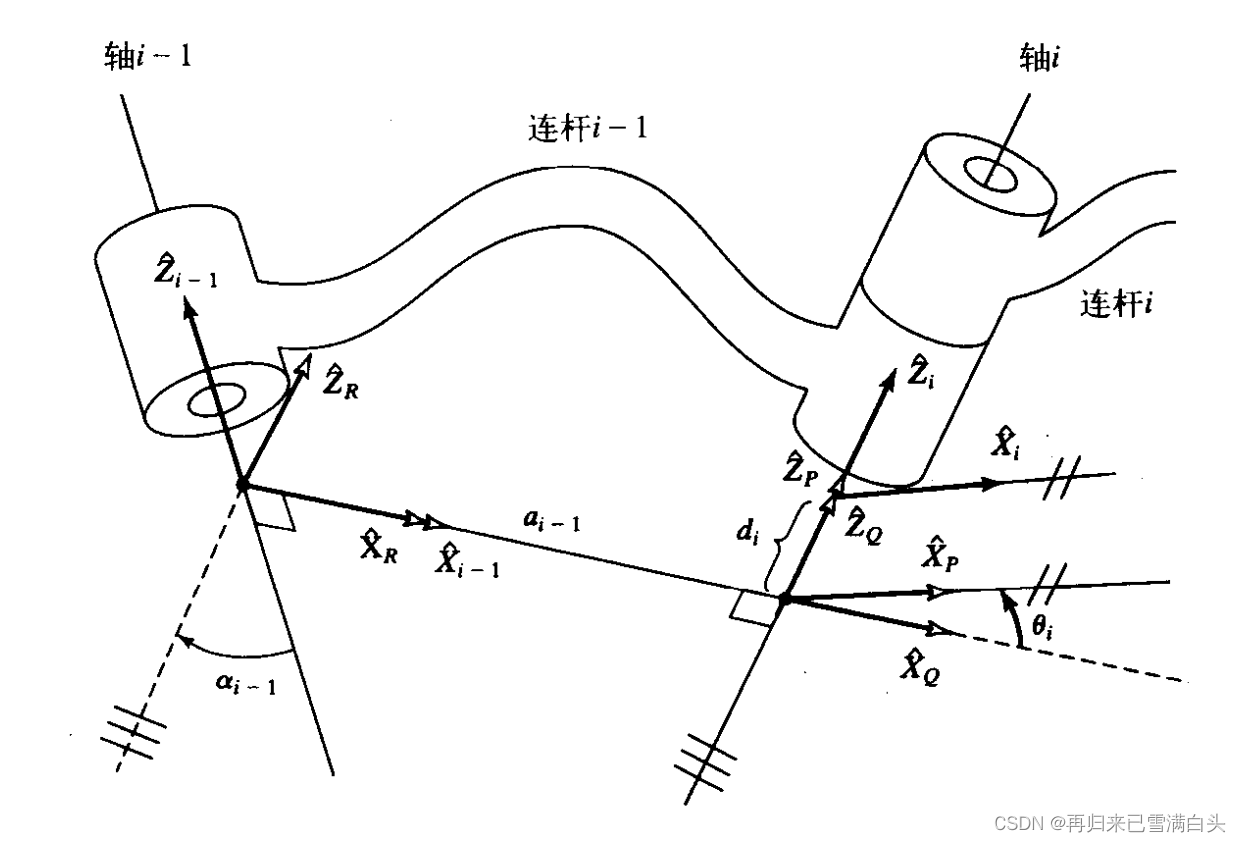
如上图，R坐标系与坐标系i-1的区别在于旋转了${\alpha }_{i-1}$，Q坐标系和R坐标系的区别在于位移$a_{i-1}$，Q坐标系与P坐标系的区别在于旋转了${\theta }_i$，P坐标系与i坐标系的区别在于平移了$d_i$。如果要把在坐标系i中定义的矢量转换为在坐标系i-1上定义的矢量，这样的变换矩阵可以写成：
$${}^{i-1}P{=}_R^{i-1}{T}_Q^{R}T{\cdot }_P^{Q}T{\cdot }_i^{P}T{\cdot }^{i}P$$
即：
$$\begin{gathered} {}^{i-1}P{=}_i^{i-1}T{\cdot }^{i}P{ \\ }_i^{i-1}T{=}_R^{i-1}{T}_Q^{R}T{\cdot }_P^{Q}T{\cdot }_i^{P}T \end{gathered}$$
考虑每个变换矩阵，有：
$${}_i^{i-1}T=R_X({\alpha }_{i-1})D_X(a_{i-1})R_Z({\theta }_i)D_z(d_i)$$
连乘后，有：
$${}_i^{i-1}T=\left(\begin{array}{cccc}cos{\theta }_i& -sin{\theta }_i& 0& a_{i-1}\\ sin{\theta }_{i}cos{\alpha }_{i-1}& cos{\theta }_{i}cos{\alpha }_{i-1}& -sin{\alpha }_{i-1}& -sin{\alpha }_{i-1}{d}_i\\ sin{\theta }_{i}sin{\alpha }_{i-1}& cos{\theta }_{i}sin{\alpha }_{i-1}& cos{\alpha }_{i-1}& cos{\alpha }_{i-1}{d}_i\\ 0& 0& 0& 1\end{array}\right)$$

经典DH描述（SDH）

机器人学导论这本书讲的是改进DH描述，然而接下来要使用的UR16e机械臂使用的是经典DH参数表。

标准DH参数和改进DH参数的区别主要在于坐标系的建立上，标准坐标系建立在link末端，$Z_i$轴沿关节轴i+1的轴向，原点$O_i$是$Z_{i-1}$轴与$Z_i$轴的交线或公垂线和关节轴$Z_i$轴的交点。$X_i$轴沿$Z_{i-1}$轴的轴线方向$Z_i$轴的公垂线方向，由关节轴i指向关节轴i+1。

由此得到的旋转矩阵为：
$${}_i^{i-1}T=\left(\begin{array}{cccc}cos{\theta }_i& -sin{\theta }_{i}cos{\alpha }_i& 0& a_{i-1}\\ sin{\theta }_i& cos{\theta }_{i}cos{\alpha }_i& -sin{\alpha }_{i}cos{\theta }_i& sin{\theta }_i{a}_i\\ 0& sin{\alpha }_i& cos{\alpha }_i& c{d}_i\\ 0& 0& 0& 1\end{array}\right)$$