运筹学Operations Research--线性规划

运筹学的核心思想：最优化；
运筹学的系统观，即全局最优化；

---

线性规划(Linear Programming)

L.P.数学模型：

• 三要素 ：决策变量、目标要求、约束条件
• 一般地，
  $Max~z=CX \\ s.t.\left\{\begin{matrix} AX\leqslant b\\ X\geqslant 0 \end{matrix}\right.$
  其中， $X$是决策变量向量，C称为价格系数向量（一般是效益等的，这里用价格）， $A$称为技术系数矩阵， $b$称为资源限制向量。
  技术系数，又称“条件约束系数”、“单耗”，来源于：A中的元素一般是资源的单耗量，各个工厂的技术不同，对应的资源单耗量也不同，所以称为技术系数。
  $s.t.$是subject to的缩写，意为约束条件。
  标准型及其转化
  
  转化需要注意：
  1. 要求目标函数用 $max$,否则对目标函数整体加负号，这样就把最小值问题转化成了最大值；
  2. 要求约束方程为等式。否则,引入松弛变量将不等式转化为等式约束。如果是 $\leq$，则在左边加入非负松弛变量；如果是 $\geq$，则在左边引入负的松弛变量。示例如下：
     标准化前：
     $max ~ z=70x_{1}+30x_{2}\\ s.t.\left\{\begin{matrix} 3x_{1}+9x_{2}\leqslant 540\\ 5x_{1}+5x_{2}\leqslant 450\\ 9x_{1}+3x_{2}\leqslant720\\ x_{1},x_{2}\geqslant0 \end{matrix}\right.$
     标准化之后：
     
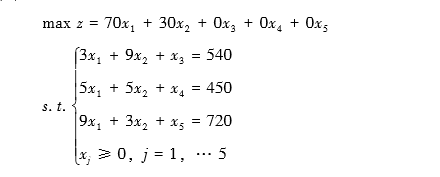
  3. 要求约束方程右边常数是非负的，否则在两边同时乘以“-1”使得约束方程右边常数变为非负。
  4. 要求所有变量非负。若 $x_{k}$为无约束变量（即可正可负），则令 $x_{k}={x}'_{k}-{x}''_{k}$，其中 ${x}'_{k},{x}''_{k}>0$即可。
  5. 例题
     
     标准化之后：
     

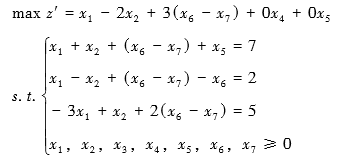
线性规划解的名称：
可行解：凡满足所有约束条件的所有解称为可行解，对应着可行方案；
可行解域：所有可行解的集合。可行解域中的任何一点，即可行点；
最优解：使得目标函数值达到最优的可行解；
基本解：所有约束条件直线的交点对应的解；
基本可行解：基本解&&可行解；

求解方法：
4. 图解法
利用数模中防护曾式的几何图形来直接找到最优解；
该方法简单直观，但只适用于两个变量；
两个变量线性规划的性质：
1. 两个变量的线性规划问题的可行域（如果存在的话）是个凸多边形（可能有界，也可能无界）；
2. 如果两个变量的线性规划问题有最优解，则最优解顶可以在可行域的某个顶点处取得。
5. 单纯形法
线性规划的通用方法。适用于多个变量，但比较抽象。

---

参考资料：爱课程·资源共享课程《运筹学》天津大学，主讲老师：杜纲*
一、单纯形法的预备知识


二、单纯形法步骤和原理


注：计算检验比向量 $\theta$时，如果有某个分量 $\theta_{i}<0$，那么就不计算这个分量，接着计算下一个分量；而，如果检验比向量中所有分量都小于零，即 $\theta<0$时，那么该LP问题就是无界解。
这一点，在下面的这道例题中有所体现：

三、单纯形表

四、大M法

它是众多人工变量法的一种。其中， $M$称为罚因子，作用是迫使所有人工变量 $X_{人}$出基（在初始时，人工变量就是基向量）。
那么，

• M为什么能做到这一点呢？
  M可以视为一个很大的数，而添加的人工变量都是非负的，那么很容易看出人工变量是阻碍原标准型的目标函数 $Max~z=CX-MX_{人}$达成目标的（目标是最大），于是，在单纯形法的迭代过程中，经过逐层优化，会使得人工变量不断地出基。

• 为什么要让人工变量出基呢？
  需要注意到，原目标 $Max~z=CX$是不包含人工变量的，要想在新模型中做到这一点，只能令 $X_{人}=0$，而非基变量在最优解中是取0的，所以只需要让人工变量出基即可。

• 人工变量构造出了单纯形法需要的单位阵 $I$，所以接下来只需要原单纯形法即可。
  

• 计算单纯性表时，注意：人工变量出基后，不会再进基，故其出基后的系数列不必再参加迭代运算，也就不用再算了。

• 

• 人工变量与松弛变量的区别：
  松弛变量是为了把不等式化成等式时加的，有实际意义–表示对应原材料的剩余量；
  而，人工变量是在等式上加的，只是为了凑出初始基矩阵 $I$（单位阵），并无实际意义。
  但二者都是非负的，满足非负约束条件。

1.2 单纯形法名词术语
结构变量――structure variable
人工变量――artificial variable
自由变量――free variable
松弛变量――slack variable
剩余变量――surplus variable
图解法――diagram method
可行域――feasible region
凸多面体――convex polyhedron
顶点（角点）――corner-point
单纯形法――Simplex method
单纯形表――simplex tableau
基――basic matrix
初始基――initial basis
可行基――feasible basis
最优基――optimal basis
基变量――basic variable
非基变量――nonbasic variable
可行解――feasible solution
基本解――basic solution
基本可行解――basic feasible solution
初始基本可行解――initial basic feasible solution
非退化基本可行解――nondegenerate basic feasible solution
最优解――optimal solution
检验数――test number
进基变量――entering basic variable
出基变量――leaving basic variable
主元――pivot number
换基迭代――basis iteration
多个最优解――multiple optimal solutions
无解――no solutions
无界――unbounded
矩阵形式――matrix form
字典序法――dictionary ordered method
布兰德法则――Bland rule
大M法――big M method
两阶段单纯形法――two-phase simplex method

---

对单纯形法的另一种表达和理解方式：

由于 $X_{B}=B^{-1}b-B^{-1}NX_{N}$(用分块矩阵表示线性规划问题的约束条件，再化简即可得到该式)。

经过对基变量进行高斯消元，从而把该线性规划问题用一种新的形式表现出来，即proper form
此时，目标函数非基变量对应的系数就是各自的检验数，

基本可行解的最优性检验：
下面所提到的式子（1.10）和（1.11）在上上张图中可以看到。

如果目标函数是min，则非基变量检验数 $\sigma_{m+k}$大于等于0变成了是我们需要的。而在目标函数max情况下，它是要出基的，也就是不需要。
单纯性表：