【运筹学】线性规划问题的解 ( 可行解 | 可行域 | 最优解 | 秩的概念 | 极大线性无关组 | 向量秩 | 矩阵秩 | 基 | 基变量 | 非基变量 | 基解 | 基可行解 | 可行基 )

I . 线性规划问题解

---

下面是一个 线性规划 数学模型 的 标准形式 :

• 1. 决策变量个数 : 线性规划数学模型中 有 $n$ 个 决策变量 ;
• 2. 约束方程个数 : 该模型中有 $m$ 个约束方程 ;

$\begin{array}{lcl} max Z = \sum_{j = 1}^n c_j x_j && ① 目标函数 \\ \\ s.t \begin{cases} \sum_{j = 1}^n a_{ij} x_j = b_i ( i = 1, 2, \cdots , m ) && ② 约束方程 \\ \\ x_j \geq 0 , j = 1 , 2 , \cdots , n && ③ 变量约束 \end{cases} \\ \end{array}$

线性规划的解 : 满足约束条件 ② 和 ③ 有很多解 , 这些解中肯定有一个或多个解 , 使 ① 目标函数 有最大值 ;

II . 可行解 与 可行域

---

可行解 : 满足 约束方程 , 变量约束 的解是可行解 ;

可行域 : 所有的可行解集合 是可行域 ;

III . 最优解

---

首先 这个解必须是可行解 , 在可行解的基础上 , 使目标函数达到最大值的解 是 最优解 ;

IV . 秩 的 概念

---

1. 向量 概念 :

• ① 数学 概念 : 空间中的箭头 , 二维 或 三维 , 由方向 和 长度 两种属性 ;
• ② 计算机 概念 : 有序的数字列表 , 这里使用的就是这种概念 , $n$ 维向量有 $n$ 个数字组成 ;

2. 向量组 : 由多个向量组成的结构 , 下面的 $\alpha_1$ 就是一个 $n$ 维向量 , 该向量由 $n$ 个数字组成 ( $n > 0$ ) ; 多个这种向量组成向量组 ;

3. 极大线性无关组 : 向量组 $T$ 中 , 如果有 一部分组 $\alpha_1 , \alpha_2 , \cdots , \alpha_3$ 满足下面两个条件 :

• ① 部分组线性无关 : $\alpha_1 , \alpha_2 , \cdots , \alpha_3$ 是线性无关的 ;
• ② 部分组线性表示 : $T$ 中的每个向量都可以由 $\alpha_1 , \alpha_2 , \cdots , \alpha_3$ 此部分组 中的一个或多个 线性表示 ; ( 如 向量组 $\beta = 2\alpha_1 + \alpha_2$ )

$\alpha_1 , \alpha_2 , \cdots , \alpha_3$ 称为向量 $T$ 的极大无关组 ;

4. 向量的秩 : 一个向量组的极大线性无关组所包含的向量个数 , 是向量组的秩 ;

• ① 如果向量组中的向量都是 $0$ 向量 , 那么其秩为 $0$ ;
• ② 向量组 $\alpha_1 , \alpha_2 , \cdots , \alpha_n$ 的秩记为 $rank \{ \alpha_1 , \alpha_2 , \cdots , \alpha_3 \}$

5. 矩阵的秩 :

• ① 方阵的秩 : 方阵是 行数 和 列数 相等的矩阵 , 其 列秩 和 行秩 是相等的 , 其 行数 = 列数 = 秩 ;
• ② 矩阵的秩 : $m \times n$ 矩阵的秩 最大取值 是 $m$ 和 $n$ 中较小的那个值 , 即 $min(m , n)$ ;
• ③ 满秩 : 如果矩阵的秩 等于 $min(m , n)$ , 那么该矩阵被称为 有满秩 , 是满秩矩阵 ;
• ④ 欠秩 : 反之 如果矩阵的秩 小于 $min(m , n)$ , 那么该矩阵 称为 秩不足 ( 欠秩 ) ;

V . 基 的概念

---

系数矩阵 : 约束方程的 系数 可以组成一个 $m \times n$ 阶 矩阵 , 即 $m$ 行 , $n$ 列 , 代表 有 $m$ 个约束方程 , 每个约束方程有 $n$ 个变量 ;

基 :

• ① 矩阵秩 : 设 $A$ 为上述 $m \times n$ 阶系数矩阵 $( m < n )$ , 其秩 为 $m$ ; ( 该矩阵的秩的最大取值是 $min(m , n)$ )
• ② 满秩矩阵 : 矩阵 $B$ 是矩阵 $A$ 的 $m$ 阶满秩子矩阵 , 其中 $|B| \not=0$ ,
  $B= \begin{bmatrix} & a_{11} & \cdots & a_{1m} \\ \\ &\vdots &\vdots &\vdots \\ \\ & a_{m1} & \cdots & a_{mm} \end{bmatrix} = ( p_1 \cdots p_m )$
• ③ 基引入 : 则称 $B$ 是线性规划问题的 一个基 ;

矩阵的阶数 : $m$ 行 $n$ 列 矩阵称为 $m \times n$ 阶矩阵 ; $m$ 行 $m$ 列方阵 , 称为 $m$ 阶矩阵 ;

$m$ 阶满秩子矩阵 :

• ① $m$ 阶 : 是指矩阵是 $m \times m$ 阶矩阵 , 其实一个 $m$ 行 $m$ 列的方阵 ;
• ② 满秩 : 该矩阵的最大秩是 $min(m , m)$ , 其秩为 $m$ 时 , 是满秩矩阵 ;
• ③ 子矩阵 : 该矩阵 $B$ ( $m \times$ m 阶矩阵 ) 是 矩阵 $A$ ( $m \times$ n 阶矩阵 ) 的子矩阵 ;

VI . 基变量 与 非基变量

---

基向量 : 设有以下系数矩阵 :

$B= \begin{bmatrix} & a_{11} & \cdots & a_{1m} \\ \\ &\vdots &\vdots &\vdots \\ \\ & a_{m1} & \cdots & a_{mm} \end{bmatrix} = ( p_1 \cdots p_m )$

称 矩阵 $B$ 中的每个列向量 $P_j ( j = 1, 2 , \cdots , m )$ 为基向量 ;

基变量 : 与 基向量 $P_j$ 对应的变量 $x_j$ 称为基变量 ;

非基变量 : 基变量之外的其它变量 , 称为 非基变量 ;

VII . 基解

---

基解 :

• ① 确定基 : 确定一个基 $B$ , 该矩阵是系数矩阵 $A$ 的满秩子矩阵 , 即一个 $m \times m$ 阶矩阵 ;
• ② 处理非基变量 : 将非基变量 设置成 $0$ ;
• ③ 解出基解 : 将 基 代入约束方程 , 解出对应的变量值 , 即基解 ;
• ④ 基解个数 : 基解中变量取值 非 $0$ 个数 , 小于等于 约束方程个数 $m$ , 基解的总数 不超过 $C_n^m$

排列组合 说明 :
$n > m$ , 从 $n$ 个变量中取 $m$ 个 , 这是集合的组合问题 , 从 $n$ 元集 中取 $m$ 个元素的个数 , 即 $C(n, m) = C_n^m =\frac{P( n, m )}{m!}=\frac{n!}{(n-m)!m!}$ , 如果要求顺序 , 就是排列问题 $P( n, m ) = \frac{n!}{(n-m)!}$ ;

$m$ 阶满秩子矩阵 : 基是满秩子矩阵

• ① $m$ 阶 : 是指矩阵是 $m \times m$ 阶矩阵 , 其实一个 $m$ 行 $m$ 列的方阵 ;
• ② 满秩 : 该矩阵的最大秩是 $min(m , m)$ , 其秩为 $m$ 时 , 是满秩矩阵 ;
• ③ 子矩阵 : 该矩阵 $B$ ( $m \times$ m 阶矩阵 ) 是 矩阵 $A$ ( $m \times$ n 阶矩阵 ) 的子矩阵 ;

VIII . 基可行解 与 可行基

---

基可行解 : 解出的基解 , 有一部分满足 变量的 非负 约束 , 即解大于等于 $0$ , 这些解称为基可行解 ;

有些解小于 $0$ 的 , 显然不满足大于等于 $0$ 的条件 , 这些基解不是可行解 , 没有用处 ;

可行基 : 基可行解 对应的基 , 称为 可行基 ;

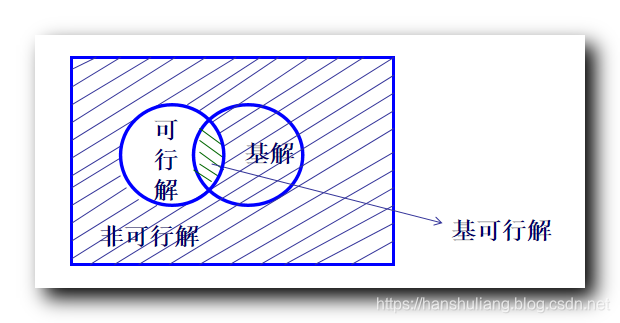
下面的文氏图 描述的是 非可行解 , 基解 , 可行解的 集合关系 ;
总体分为 可行解 与 非可行解 , 基解中一部分是可行解 , 一部分是非可行解

IX . 示例 求基矩阵

---

求下列线性规划问题的 基矩阵 :

$\begin{array}{lcl} max Z = 4x_1 - 2x_2 - x_3 \\\\ \begin{cases} 5x_1 + x_2 - x_3 + x_4 = 3 \\\\ -10 x_1 + 6x_2 + 2x_3 +x_5 = 2 \\\\ x_j \geq 0 , j = 1 , \cdots , 5 \end{cases} \end{array}$

解 :

该约束方程 , 共有 $x_1 , x_2 , x_3 , x_4 , x_5$ , 五个变量 ;

将约束方程补全变量为 :
$\begin{cases} 5x_1 + x_2 - x_3 + x_4 + 0x_5= 3 \\\\ -10 x_1 + 6x_2 + 2x_3 + 0x_4 +x_5 = 2 \end{cases}$

其系数矩阵为 :
$A=\begin{bmatrix} 5 & 1 & -1 & 1 & 0 \\\\ -10 & 6 & 2 & 0 & 1 \end{bmatrix}$

该系数矩阵的秩为 $min(2, 5) = 2$ , 矩阵的基为 2阶满秩子矩阵 ;
每一列都是一个 向量 , 共有 5 个向量 , 选择其中 2 个 , 该问题是 从 5 元集 中选取 2 个的 组合问题 ;
其基的组合方式有 $C(5 , 2)$ 种 :
$C(5 , 2) = \frac{5!}{2! ( 5 - 2 )!} = \frac{5 \times 4 \times 3 \times 2}{2\times 3\times 2} = 10$

2阶子矩阵有 $10$ 种 选取方式 ; 基的要求还需要 满秩 , 2阶的满秩子矩阵 才是基 , 满秩 即 其列向量 线性无关 , 两列 向量 不能使用线性表示 ;

① 子矩阵 1 : ( 不是基矩阵 )
$B_1 = \begin{bmatrix} 5 &-1 \\ -10 & 2\end{bmatrix}$
注意 该矩阵 第一列 与 第二列 存在线性关系 , 第一列向量 乘以 $-5$ 即可得到第二列向量 ;
$B_{11} = \begin{bmatrix} 5 \\ -10\end{bmatrix} B_{12} = \begin{bmatrix} -1 \\ 2\end{bmatrix}$
$B_{12} = -5 \times B_{11}$

该矩阵的秩为 $1$ , 不是满秩的 , 满秩秩为 $min(2 , 2) = 2$ , 因此该矩阵不是基矩阵 ;

② 子矩阵 $2 \cdots 9$ : 其它矩阵 列向量 之间没有线性关系 , 都是满秩的 , 且都为 $2$ 阶满秩子矩阵
$B_2 = \begin{bmatrix} 5 &1 \\ -10 & 6\end{bmatrix}$
$B_3 = \begin{bmatrix} 5 &0 \\ -10 & 1\end{bmatrix}$
$B_4 = \begin{bmatrix} 5 &1 \\ -10 & 0\end{bmatrix}$
$B_5 = \begin{bmatrix} 1 &-1 \\ 6 & 2\end{bmatrix}$
$B_6 = \begin{bmatrix} 1 &1 \\ 6 & 0\end{bmatrix}$
$B_7 = \begin{bmatrix} 1 & 0 \\ 6 & 1\end{bmatrix}$
$B_8 = \begin{bmatrix} -1 &1 \\ 2 & 0\end{bmatrix}$
$B_9 = \begin{bmatrix} -1 &0 \\ 2 & 1\end{bmatrix}$
$B_{10} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$

该矩阵 $B_2 \cdots B_{10}$ 是系数矩阵的 2阶满秩子矩阵 ;