1.问题提出
- 软件行业中客户总是在变更需求
银行对我们公司开发的乘法模块还不满意。他们的真实想法并不是实现两个矩阵的乘法,而是是能一次够实现多个矩阵按照算法运算法则的乘法,因此要求我们进一步改进我们的系统,实现多个矩阵的连乘功能,并且需要看到我们设计的程序能够满足他们的运行效率要求时才付二期款。
2.关键计算问题
- 给定n个矩阵{
,
,。。。
}, 其中
与
是可乘的,i=1,2,…n-1。 考察这n个矩阵的连乘积
… - 由于矩阵乘法满足结合律,所以计算矩阵的连乘可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定
- 若一个矩阵连乘积的计算次序完全确定,也就是说该连乘积已完全加括号,则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积
3.完全加括号的矩阵连乘积
-
设有四个矩阵 A,B,C,D, 它们的维数分别是:
A=5010 ,B =1040 ,C = 4030 D = 305 -
总共有五中完全加括号的方式,及相应的乘法次数如下
(A((BC)D))------------16000
(A(B(CD))) ------------10500
((AB)(CD))-----------36000
(((AB)C)D) ------------87500
((A(BC))D)--------------34500 -
对于 pXq 矩阵 A 和一个 qXr 矩阵 B, AB 需要 ? 标准乘法计算。
标准乘法次数是:pqr,即:A的行乘以B的行乘以B的列这么多次
理解:用A的一行乘以B的所有列,总共是pr次,但是A有q个行,所以最终是pr*q

//java编写
matrixMultiply(int [][]a,int [][]c, int ra,int ca,int rb,int cb)
{
if (ca!=rb)
Throw new IllegalArgumentException(“矩阵不可乘” );
for(int i=0;i<ra;i++)//ra是矩阵A的行
{
for(int j=0;j<cb;j++)//cb是矩阵B的列
{
int sum=a[i][0]*b[0][j];
for(int k=1;k<rb;k++)//rb是B的行
{
Sum+=a[i][k]*b[k][j];
c[i][j]=sum;
}
}
}
}
- eg:如果 A1, A2, and A3 是 20X100, 100X10, 和 10X50 矩阵,A1XA2XA3乘积运算次数是多少?

4.矩阵连乘问题
-
给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2 ,…,n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。
-
穷举法求解思路
穷举法:列举出所有可能的计算次序, 并计算出每一种计算次序相应需要的数乘次数,从中找出一种数乘次数最少的计算次序。
算法复杂度分析:
对于n个矩阵的连乘积,设其不同的计算次序为P(n)。
由于每种加括号方式都可以分解为两个子矩阵的加括号问题:
((A1…Ak)(Ak+1…An))可以得到关于P(n)的递推式如下,k可以取1到n
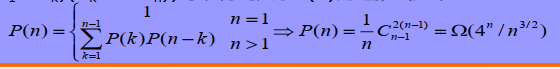
Catalan 数 P(n) = C(n-1)
5.用动态规划思想求解问题?
-
(1)分析最优解的结构
将矩阵连乘积 AiAi+1…Aj简记为A[i:j] ,这里i≤j。考察计算A[i:j]的最优计算次序。
设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开, i≤k<j,则其相应完全加括号方式为(AiAi+1…Ak )(Ak+1Ak+2…Aj )
所以:总计算量=A[i:k]的计算量加上A[k+1:j]的计算量,再加上A[i:k]和A[k+1:j]相乘的计算量 -
(2)分析最优解的子问题结构
特征:计算A[i:j]的最优次序所包含的计算矩阵子链 A[i:k]和A[k+1:j]的次序也是最优的。
但是子问题不独立,适合动态规划算法设计,因为eg:假设计算A[1:4],其可被分解为A[1:2]和A[2:4],但是同时都覆盖了矩阵A[2]
矩阵连乘计算次序问题的最优解包含着其子问题的最优解,这种性质称为最优子结构性质。 -
(3)建立递推关系
递推关系式是通过最优值来构建的!!不是通过最优解构建的!!
设计算A[i:j], 1≤k≤j≤n,所需要的最少数乘次数m[i,j],则原问题的最优值为m[1,n]
当i=j时,A[i:j]= ,so,m[i:j]=0,i=1,2,。。。,n
当i<j时,m[i,j]= {m[i,k]+m[k+1,j]+pi-1 * },这里 的维数为pi-1 * pi
可以递归地定义m[i,j]为: -
以自底向上的方式计算出最优值到底是干嘛?
子问题规模最小的地方就是底,沿着反的递归方向往上合并的过程,逐个让子问题的规模变大,形成大问题的解,最终合成最终原来的解
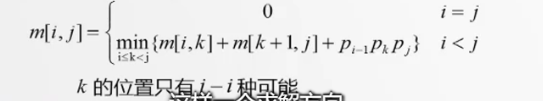
-
(4)建立递归算法
根据上面的递归式与前面的分治递归部分学到的算法设计知识,建立递归算法 -
(5)实际子问题数目
首先分析一下递归算法消耗指数计算的时间
对于1≤k≤j≤n,不同的有序对(i,j)对应于不同的子问题。因此,不同子问题的个数最多有:
,因为要形成两个矩阵的乘法过程(Ai)*(Aj),相当于每次在n个这样的数当中选出2个数,来把它分开的过程就是问题个数,还要加上n个单独Ai矩阵的乘法
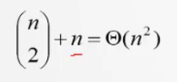
由此可见,在递归算法中,有许多的子问题被重复计算多次。 这也是该问题可用动态规划算法求解的又一显著特征。
用动态规划算法求解此问题, 可以依据其递归式以自底向上的方式进行计算。在计算过程中,保存已解决的子问题答案,每个子问题只计算一次, 而在后面需要时只要简单查一下,从而避免大量的重复计算,最终得到多项式时间的算法。
递归是从上至下的,从上面的大问题逐个分解成最小规模的子问题,动态规划问题是从下至上,不断合并子问题
-
动态规划求最优解
public static matrixChain(int [] p,int [][] m,int [][] s)
{
int n=p.length-1;
for (int i=1;i<=n;i++)//首先求解最小子问题的答案,i=j时,后面可以查表获取答案
m[i][i]=0;
//下面是m[i,i+r]的子问题,让i到j之间的距离,逐个从2增加到n,逐个扩大子问题的规模
//>=3个矩阵开始
for (int r=2;r<=n;r++)//复杂度为n
{
for(int i=1;i<=n-r+1;i++)//复杂度为n
{
//因为要计算min,所以这里计算了一个参考值
//i=1,j=2,两个矩阵相乘
int j=i+r-1;
m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];
s[i][j]=i;
for (int k=i+1;k<j;k++)//复杂度为k
{
int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];//最优的m[i,j]
if (t<m[i][j])
{
m[i][j]=t;//形成最小,最优的m[i][j]
s[i][j]=k;//存储了计算过程中的最优值的形成过程,通过s[i][j]可以反向获取最优解
}
}
}
}
}
算法的复杂度分析:
算法的主要计算量取决于算法中对r,i和k的3重循环。循环体内的计算量为O(1),而三重循环的总次数为
O(n^3),因此算法的计算时间上界是O(n^3),算法所占用的空间为O(n^2),因为是二维的矩阵
- eg说明:下表6个矩阵连乘问题

说明:
A2*(A3A4A5),此时k=2;
(A2A3)*(A4A5),此时k=3
(A2A3A4)*A5,此时k=4
若k=2进行断开,在计算m[2][5]之前,肯定计算了m[2][2]和m[3][5],其值存在了(b)表中,
所以计算m[2][2]完全可以通过查表来获得,s[i][j]标识了m[3][5]加括号的最优解,
是在3的位置进行了一个分段,所以m[3][5]的乘法过程是A3*(A4A5),而A4*A5是5*20,
A3*(A4A5)是15*20,最终还要乘以A2,就为35*15*20
若k=3进行断开,查表可以得到m[2][3],m[4][5],后面的值:A2*A3=35*5,A4*A5=5*20,所以最终
是35*5*20
min[2][5]=min{13000,7125,11375}
算完m[2][5],还可以算m[2][6]
所以最优值是m[1][6]
