信号与系统公式笔记（4）

截图基本上都是来自b站av5868266，齐开悦博士的讲义。
之前的笔记（第二章）重要的是两点：微分方程和卷积（微分方程要理解好，卷积熟练会用就行）。

这次主要是关于连续信号的傅里叶分析（教材里面有三大变换：傅里叶、拉普拉斯、Z，拉普拉斯其实是连续傅里叶的推广，Z其实是离散傅里叶变换的推广。重点还是三大变换）。

重点内容：

连续时间周期信号的傅里叶级数
连续时间建立傅里叶变换
傅里叶级数与傅里叶变换之间的关系
傅里叶变换的性质
系统的频率响应及系统的频域分析
采样（抽样）及采样（抽样）处理
计算傅里叶系数的公式

这一章要解决的问题：对非周期信号应该如何进行分解、什么是非周期信号的频谱表示

傅里叶变换的思想：
1. 周期信号都可以表示为成谐波关系的正弦信号的加权和
2. 非周期信号都可以用正弦信号的加权积分来表示

成谐波关系的复指数信号集： $\phi_k(t) = \mathrm{e}^{jk\omega_0t}$ ，这些信号的公共周期是 $\frac{2\pi}{|\omega_0|}$ 。
将所有信号线性组合（类似上面的思想）：

x (t) = \sum_{k = - \infty}^{\infty} a_{k} e^{j k ω_{0} t}

$x(t) = \sum_{k = -\infty}^{\infty}a_k\mathrm{e}^{\mathrm{j}k\omega_0t}$

其实上面这个就是傅里叶级数， $a_k$ 就是傅里叶级数的系数。
可以总结成：连续时间周期信号可以分解成无数多个复指数的谐波分量。

傅里叶级数的系数 $a_k$ 就是信号分量的幅度，所以可以用这些幅度画成频谱。
频谱图：

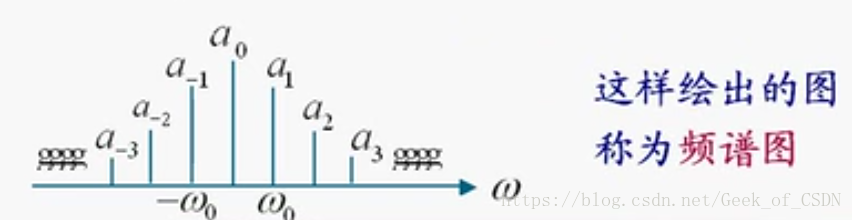
补充个欧拉公式：

e^{j ω t} = \cos ω t + j \sin ω t

$\mathrm{e}^{\mathrm{j}\omega t} = \cos{\omega t} + \mathrm{j}\sin{\omega t}$

经常用这个公式在复指数和三角函数之间转换，所以必须要记。

三角函数集：
$\cos(n\omega_1t), \sin(n\omega_1t)$ 是完备的正交函数集，具体的证明可以看教材，其实就是几个三角函数相乘，然后在一个周期内积分的证明（因为是正交的，所以积分结果为0）。

完备正交函数集指的是除了花括号里面括起来的那一对以外，集合里面没有别的函数能与这一对正交（ $n$ 可以取任意整数）。

在满足狄氏条件的前提下可以将指数级数展开成三角形式（记公式）。
公式：

f (t) = a_{0} + \sum_{n = 1}^{\infty} [a_{n} \cos (n ω_{1} t) + b_{n} \sin (n ω_{1} t)]

$f(t) = a_0 + \sum_{n = 1}^{\infty}[a_n\cos(n\omega_1 t) + b_n\sin{(n\omega_1t)}]$
上面的系数用下面的公式求出来
直流分量

a_{0} = \frac{1}{T} \int_{t_{0}}^{t_{0} + T} f (t) d t

$a_0 = \frac{1}{T}\int_{t_0}^{t_0 + T}f(t)\mathrm{d}t$
余弦分量的幅度

a_{n} = \frac{2}{T} \int_{t_{0}}^{t_{0} + T} f (t) \cos (n ω_{1} t) d t

$a_n = \frac{2}{T}\int_{t_0}^{t_0+T}f(t)\cos(n\omega_1t)\mathrm{d}t$
正弦分量的幅度

b_{n} = \frac{2}{T} \int_{t_{0}}^{t_{0} + T} f (t) \sin (n ω_{1} t) d t

$b_n = \frac{2}{T}\int_{t_0}^{t_0+T}f(t)\sin(n\omega_1t)\mathrm{d}t$
补充一下，上面式子里面的

\frac{2}{T}

$\frac{2}{T}$ 其实就是

\int_{t}^{t + T} \sin m ω_{1} \sin n ω_{1} t d t = \frac{T}{2}, m = n \neq 0

$\int_{t}^{t + T}\sin{m\omega_1}\sin{n\omega_1 t}\mathrm{d}t = \frac{T}{2}, \quad m = n\neq0$ ，下面的复指数公式里面出现的

\frac{1}{T}

$\frac{1}{T}$ 其实也差不多
例题：齐开悦博士第三章课件例1

其他形式：
用公式直接转化成只有正弦或者余弦表达的形式
用到的公式
余弦形式：

f (t) = c_{0} + \sum_{n = 1}^{\infty} c_{n} \cos (n ω_{1} t + φ_{n})

$f(t) = c_0 + \sum_{n = 1}^{\infty}c_n\cos(n\omega_1 t + \varphi_n)$
里面的系数可以用下面公式求

c_{0} = a_{0} c_{n} = \sqrt{a_{n}^{2} + b_{n}^{2}} φ_{n} = \arctan (\frac{- b_{n}}{a_{n}})

$c_0 = a_0\quad c_n = \sqrt{a_n^2 + b_n^2}\quad \varphi_n = \arctan(\frac{-b_n}{a_n})$
可以联想成三角形来记
反过来

a_{n} = c_{n} \cos φ_{n} b_{n} = - c_{n} \sin φ_{n}

$a_n = c_n\cos\varphi_n \quad b_n = -c_n\sin\varphi_n$

正弦形式

f (t) = d_{0} + \sum_{n = 1}^{\infty} d_{n} \sin (n ω_{1} t + θ_{n})

$f(t) = d_0 + \sum_{n = 1}^{\infty}d_n\sin(n\omega_1t + \theta_n)$
系数

d_{0}

$d_0$ 、

d_{n}

$d_n$ 和余弦的差不多，其他可以用下面的公式来求：

θ_{n} = \arctan (\frac{b_{n}}{a_{n}})

$\theta_n = \arctan(\frac{b_n}{a_n})$
反过来

a_{n} = d_{n} \sin (θ_{n}) b_{n} = d_{n} \cos (θ_{n})

$a_n = d_n\sin(\theta_n) \quad b_n = d_n\cos(\theta_n)$

其实上面用的还是三角函数合并用到的公式，实在记不得也可以推导出来，只是记得的话方便一点。

这样就可以把周期信号分解成直流、基波（ $\omega_1$ ）和各次谐波（ $n\omega_1$ ：基波角频率的整数倍）的线性组合。

然后用 $c_n ~ \omega$ 关系画成幅度频谱图
$\varphi_n ~ \omega$ 关系画成相位频谱图（这些符号代表的意思上面的公式里面都有）

周期信号频谱具有离散性、谐波性、收敛性。

指数形式的傅里叶级数

复指数正交函数集 ${\mathrm{e}^{\mathrm{j}n\omega_1 t}}\quad n = 0, \pm1, \pm2\cdots$
级数形式：

f (t) = \sum_{n = - \infty}^{\infty} F (n ω_{1}) e^{j n ω_{1} t}

$f(t) = \sum_{n = -\infty}^{\infty}F(n\omega_1)\mathrm{e}^{\mathrm{j}n\omega_1t}$
上面公式里面的

F (n ω_{1})

$F(n\omega_1)$ 系数用下面这个公式来确定：

F (n ω_{1}) = \frac{\int_{0}^{T_{1}} f (t) e^{- j n ω_{1} t} d t}{\int_{0}^{T_{1}} e^{j n ω_{1} t} e^{- j n ω_{1} t} d t} = \frac{1}{T} \int_{0}^{T_{1}} f (t) e^{- j n ω_{1} t} d t

$F(n\omega_1) = \frac{\int_{0}^{T_1}f(t)\mathrm{e}^{-\mathrm{j}n\omega_1t}\mathrm{d}t}{\int_{0}^{T_1}\mathrm{e}^{\mathrm{j}n\omega_1t}\mathrm{e}^{-\mathrm{j}n\omega_1t}\mathrm{d}t} = \frac{1}{T}{\int_{0}^{T_1}f(t)\mathrm{e}^{-\mathrm{j}n\omega_1t}\mathrm{d}t}$
其实

F (n ω_{1})

$F(n\omega_1)$ 也可以写成

F_{n}

$F_n$ 。

上面复指数和三角函数之间可以直接用欧拉公式进行转换。

上面公式里面出现了 $-1$ 是因为 $\mathrm{j} * \mathrm{j} = -1$ ， $\sin$ 部分多了个 $\mathrm{j}$ 。
欧拉公式：

e^{j ω t} = \cos ω t + j \sin ω t

$\mathrm{e}^{\mathrm{j}\omega t} = \cos{\omega t} +\mathrm{j} \sin{\omega t}$

了解就行。

上面几个系数之间的关系

上图中奇偶函数的定法可以直接看原公式得出。

总结
周期信号 $f(t)$ 胡傅里叶级数两种形式：
三角形式：

f (t) = a_{0} + \sum_{n = 1}^{\infty} [a_{n} \cos (n ω_{1} t) + b_{n} \sin (n ω_{1} t)] = c_{0} + \sum_{n = 1}^{\infty} c_{n} \cos (n ω_{1} t + φ_{n})

$f(t) = a_0 + \sum_{n = 1}^{\infty}[a_n\cos(n\omega_1t) + b_n \sin(n\omega_1 t)] = c_0 + \sum_{n = 1}^{\infty}c_n\cos(n\omega_1t + \varphi_n)$
其实最后面也可以转成

\sin

$\sin$ 的形式

指数形式：

f (t) = \sum_{n = - \infty}^{\infty} F (n ω_{1}) e^{j n ω_{1} t}

$f(t) = \sum_{n = -\infty}^{\infty}F(n\omega_1)\mathrm{e}^{\mathrm{j}n\omega_1t}$

两种频谱图的关系

注意画频谱图的时候用的是 $c_n ~ \omega$ ，不是 $d_n$ ，所以要吧 $\sin$ 的部分转成 $\cos$ 。

基本上就是套上面的公式。

指数形式频谱里面出现的负频率的存在只是为了使公式有数学意义，其实没有物理意义，是用来保证 $f(t)$ 的实函数性质。

傅里叶级数有三个性质
收敛性（ $n\uparrow, |F(n\omega_1)| \downarrow$ ）
谐波性/离散性
唯一性（ $f(t)$ 谱线唯一）

补充：冲激函数序列的频谱不满足收敛性。

信号与系统公式笔记（4）

猜你喜欢