连续周期信号
f
(
t
)
f(t)
f ( t )
T
T
T
f
(
t
)
=
f
(
t
+
m
T
)
,
m
=
0
,
±
1
,
±
2
,
…
f(t) = f(t + mT), \ m = 0, \pm 1, \pm 2, \dots
f ( t ) = f ( t + m T ) , m = 0 , ± 1 , ± 2 , …
典型周期连续信号: 余弦信号
cos
ω
t
\cos \omega t
cos ω t
T
=
2
π
ω
(
s
)
T = \frac{2\pi}{\omega}(s)
T = ω 2 π ( s )
离散周期信号
f
(
k
)
f(k)
f ( k )
N
N
N
f
(
k
)
=
f
(
k
+
m
N
)
,
m
=
0
,
±
1
,
±
2
,
…
f(k) = f(k +mN), \ m = 0, \pm 1, \pm 2, \dots
f ( k ) = f ( k + m N ) , m = 0 , ± 1 , ± 2 , …
连续信号
f
(
t
)
=
5
e
−
0.8
t
sin
(
π
t
)
,
0
<
t
<
5
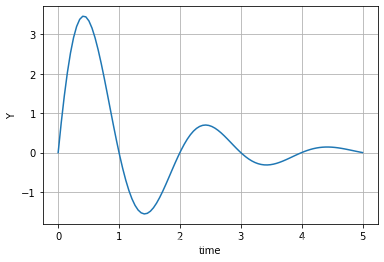
f(t) = 5 e^{-0.8t} \sin(\pi t), \, 0<t<5
f ( t ) = 5 e − 0 . 8 t sin ( π t ) , 0 < t < 5
import numpy as np
import matplotlib. pyplot as plt
import scipy. signal as sg
a, b = 0.8 , 5
t = np. linspace( 0 , 5 , 100 )
y = b* np. exp( - a* t) * np. sin( np. pi* t)
plt. xlabel( 'time' )
plt. ylabel( 'Y' )
plt. plot( t, y)
plt. grid( True )
plt. show( )
将信号
f
(
t
)
f(t)
f ( t )
1
Ω
1 \Omega
1 Ω
∣
f
(
t
)
∣
2
\lvert f(t) \rvert ^2
∣ f ( t ) ∣ 2
(
−
∞
,
∞
)
( -\infty, \infty)
( − ∞ , ∞ ) 能量 和平均功率 定义为
E
=
d
e
f
∫
−
∞
∞
∣
f
(
t
)
∣
2
d
t
E \overset{def}{=} \int_{-\infty}^\infty \lvert f(t) \rvert ^2 dt
E = d e f ∫ − ∞ ∞ ∣ f ( t ) ∣ 2 d t
P
=
d
e
f
lim
T
→
∞
1
T
∫
−
T
/
2
T
/
2
∣
f
(
t
)
∣
2
d
t
P \overset{def}{=} \lim_{T \to \infty} \frac{1}{T} \int_{-T/2}^{T/2} \lvert f(t) \rvert ^2 dt
P = d e f T → ∞ lim T 1 ∫ − T / 2 T / 2 ∣ f ( t ) ∣ 2 d t
能量有限信号 : 信号的能量
E
<
∞
E < \infty
E < ∞ 能量信号 , 此时
P
=
0
P = 0
P = 0
离散:
E
=
∑
k
=
−
∞
∞
∣
f
(
k
)
∣
2
<
∞
E = \displaystyle\sum_{k=-\infty}^{\infty} \lvert f(k) \rvert ^2 < \infty
E = k = − ∞ ∑ ∞ ∣ f ( k ) ∣ 2 < ∞
功率有限信号 : 信号的功率
P
<
∞
P < \infty
P < ∞ 功率信号 , 此时
E
=
∞
E = \infty
E = ∞
离散:
P
=
lim
N
→
∞
1
N
∑
k
=
−
N
/
2
N
/
2
∣
f
(
k
)
∣
2
<
∞
P = \displaystyle \lim_{N \to \infty} \frac{1}{N} \sum_{k=-N/2}^{N/2} \lvert f(k) \rvert ^2 < \infty
P = N → ∞ lim N 1 k = − N / 2 ∑ N / 2 ∣ f ( k ) ∣ 2 < ∞
因果信号 :
t
<
0
,
f
(
t
)
=
0
t <0, \ f(t) = 0
t < 0 , f ( t ) = 0
反因果信号 :
t
≤
0
,
f
(
t
)
=
0
t \leq 0, \ f(t) = 0
t ≤ 0 , f ( t ) = 0
一维信号, 多维信号; 实信号,复信号; 左信号, 右信号。。。。。。
1.2.6. Remark
时限信号为能量信号
周期信号为功率信号
非周期信号 可能为能量也可能为功率信号
f
(
t
)
=
e
t
f(t) = e^t
f ( t ) = e t
δ
(
x
)
=
d
e
f
{
0
,
x
≠
0
1
,
x
=
0
\begin{aligned} \delta (x) \overset{def}{=} {\begin{cases} 0 , & x\neq 0 \\ 1 , & x = 0 \end{cases}} \end{aligned}
δ ( x ) = d e f { 0 , 1 , x = 0 x = 0
单位冲激函数 : 奇异函数, 强度极大, 作用时间极短的物理量的理想化模型
{
δ
(
x
)
=
0
,
x
≠
0
∫
−
∞
∞
δ
(
x
)
d
x
=
1
\begin{aligned} {\begin{cases} \delta (x) = 0 , & x\neq 0 \\ \int_{-\infty}^{\infty} \delta(x) dx = 1 \end{cases}} \end{aligned}
{ δ ( x ) = 0 , ∫ − ∞ ∞ δ ( x ) d x = 1 x = 0
aka Dirac delta function
高度无穷大, 宽度无穷小, 面积为 1 的对称窄脉冲
阶跃函数 :
ε
(
t
)
=
d
e
f
{
0
,
t
<
0
1
,
t
>
0
\varepsilon(t) \overset{def}{=} {\begin{cases} 0, & t<0 \\ 1, & t>0 \end{cases}}
ε ( t ) = d e f { 0 , 1 , t < 0 t > 0
积分:
∫
−
∞
t
ε
(
τ
)
d
τ
=
t
⋅
ε
(
t
)
\int_{-\infty}^{t} \varepsilon(\tau)d\tau = t \cdot \varepsilon(t)
∫ − ∞ t ε ( τ ) d τ = t ⋅ ε ( t )
与 冲激函数 关联:
δ
(
t
)
=
d
ε
(
t
)
d
t
\delta(t) = \frac{d \varepsilon(t)}{dt}
δ ( t ) = d t d ε ( t )
ε
(
t
)
=
∫
−
∞
t
δ
(
τ
)
d
τ
\varepsilon(t) = \int_{-\infty}^{t} \delta(\tau) d\tau
ε ( t ) = ∫ − ∞ t δ ( τ ) d τ
Dirac Delta function 广义函数定义 :
∫
−
∞
∞
δ
(
t
)
φ
(
t
)
d
t
=
φ
(
0
)
\int_{-\infty}^{\infty} \delta(t) \varphi(t)dt = \varphi(0)
∫ − ∞ ∞ δ ( t ) φ ( t ) d t = φ ( 0 )
冲激函数
δ
(
t
)
\delta (t)
δ ( t )
φ
(
t
)
\varphi (t)
φ ( t )
φ
(
0
)
\varphi (0)
φ ( 0 )
例如:
高斯函数
δ
(
t
)
=
lim
b
→
∞
b
e
−
π
(
b
⋅
t
)
2
\delta(t) = \lim_{b\to \infty} b e^{-\pi(b\cdot t)^2}
δ ( t ) = lim b → ∞ b e − π ( b ⋅ t ) 2
取样函数
δ
(
t
)
=
lim
b
→
∞
sin
(
b
t
)
π
t
\delta(t) = \lim_{b\to \infty} \frac{\sin(bt)}{\pi t}
δ ( t ) = lim b → ∞ π t sin ( b t )
Dirac Delta function 取样性质 :
f
(
t
)
δ
(
t
−
a
)
=
f
(
a
)
δ
(
t
−
a
)
⟶
f
(
t
)
δ
(
t
)
=
f
(
0
)
δ
(
t
)
f(t) \delta(t-a) = f(a) \delta(t-a) \longrightarrow f(t) \delta(t) = f(0) \delta(t)
f ( t ) δ ( t − a ) = f ( a ) δ ( t − a ) ⟶ f ( t ) δ ( t ) = f ( 0 ) δ ( t )
∫
−
∞
∞
f
(
t
)
δ
(
t
−
a
)
d
t
=
f
(
a
)
⟶
∫
−
∞
∞
f
(
t
)
δ
(
t
)
d
t
=
f
(
0
)
\int_{-\infty}^{\infty} f(t) \delta(t-a) dt = f(a) \longrightarrow \int_{-\infty}^{\infty} f(t) \delta(t) dt = f(0)
∫ − ∞ ∞ f ( t ) δ ( t − a ) d t = f ( a ) ⟶ ∫ − ∞ ∞ f ( t ) δ ( t ) d t = f ( 0 )
Notice: 积分区间要包含
t
=
a
t=a
t = a
Dirac Delta function 导数 :
冲激偶
δ
′
(
t
)
\delta^\prime (t)
δ ′ ( t )
f
(
t
)
δ
′
(
t
)
=
f
(
0
)
δ
′
(
t
)
−
f
′
(
0
)
δ
(
t
)
f(t) \delta^\prime (t) = f(0)\delta^\prime(t) - f^\prime(0)\delta(t)
f ( t ) δ ′ ( t ) = f ( 0 ) δ ′ ( t ) − f ′ ( 0 ) δ ( t )
∫
−
∞
∞
f
(
t
)
δ
′
(
t
)
d
t
=
−
f
′
(
0
)
\int_{-\infty}^{\infty} f(t) \delta^\prime(t) dt = - f^\prime(0)
∫ − ∞ ∞ f ( t ) δ ′ ( t ) d t = − f ′ ( 0 )
∫
−
∞
∞
f
(
t
)
δ
′
(
t
−
a
)
d
t
=
−
f
′
(
a
)
\int_{-\infty}^{\infty} f(t) \delta^\prime(t-a) dt = - f^\prime(a)
∫ − ∞ ∞ f ( t ) δ ′ ( t − a ) d t = − f ′ ( a )
∫
−
∞
∞
f
(
t
)
δ
(
n
)
(
t
)
d
t
=
(
−
1
)
n
f
(
n
)
(
0
)
\int_{-\infty}^{\infty} f(t) \delta^{(n)}(t) dt = (-1)^nf^{(n)}(0)
∫ − ∞ ∞ f ( t ) δ ( n ) ( t ) d t = ( − 1 ) n f ( n ) ( 0 )
Dirac Delta function 尺度变化 :
δ
(
a
t
)
=
1
∣
a
∣
δ
(
t
)
\delta(at) = \frac{1}{\lvert a \rvert} \delta(t)
δ ( a t ) = ∣ a ∣ 1 δ ( t )
δ
(
n
)
(
a
t
)
=
1
∣
a
∣
1
a
n
δ
(
n
)
(
t
)
\delta^{(n)} (at) = \frac{1}{\lvert a \rvert} \frac{1}{a^n} \delta^{(n)}(t)
δ ( n ) ( a t ) = ∣ a ∣ 1 a n 1 δ ( n ) ( t )
f
(
t
)
→
LTI (linear time-invariant systems)
→
y
(
t
)
f(t) \to \text{LTI (linear time-invariant systems)} \to y(t)
f ( t ) → LTI (linear time-invariant systems) → y ( t )
y
(
n
)
(
t
)
+
a
n
−
1
y
(
n
−
1
)
(
t
)
+
⋯
+
a
1
y
(
1
)
(
t
)
+
a
0
y
(
t
)
=
b
m
f
(
m
)
(
t
)
+
b
m
−
1
f
(
m
−
1
)
(
t
)
+
⋯
+
b
1
f
(
1
)
(
t
)
+
b
0
f
(
t
)
y^{(n)}(t) + a_{n-1}y^{(n-1)}(t)+\dots + a_1y^{(1)}(t) + a_0y(t) \\ = b_mf^{(m)}(t)+b_{m-1}f^{(m-1)}(t) + \dots + b_1f^{(1)}(t) +b_0f(t)
y ( n ) ( t ) + a n − 1 y ( n − 1 ) ( t ) + ⋯ + a 1 y ( 1 ) ( t ) + a 0 y ( t ) = b m f ( m ) ( t ) + b m − 1 f ( m − 1 ) ( t ) + ⋯ + b 1 f ( 1 ) ( t ) + b 0 f ( t )
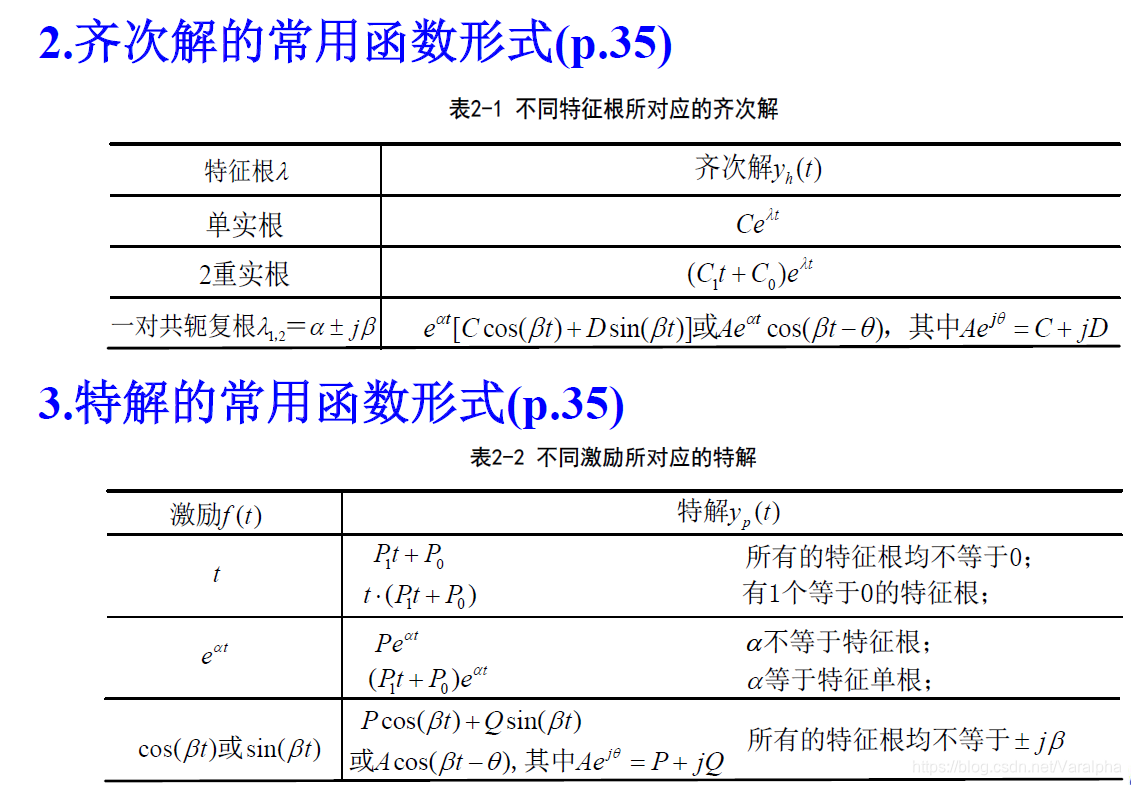
经典解法 :
y
(
t
)
=
y
h
(
t
)
+
y
p
(
t
)
y(t) = y_h(t) + y_p(t)
y ( t ) = y h ( t ) + y p ( t )
y
(
t
)
y(t)
y ( t ) 完全解
y
h
(
t
)
y_h(t)
y h ( t ) 齐次解 homogeneous solution
y
p
(
t
)
y_p(t)
y p ( t ) 特解
特征根 : eigenvalue 特征值
λ
n
+
a
n
−
1
λ
n
−
1
+
⋯
+
a
0
=
0
→
λ
i
(
i
=
1
,
2
,
…
,
n
)
\lambda^n + a_{n-1}\lambda^{n-1} + \dots + a_0 = 0\, \to\, \lambda_i(i=1,2,\dots, n)
λ n + a n − 1 λ n − 1 + ⋯ + a 0 = 0 → λ i ( i = 1 , 2 , … , n )
初始值 : 是n阶系统在
t
=
0
t=0
t = 0
t
=
0
+
t=0_+
t = 0 +
y
(
j
)
(
0
+
)
(
j
=
0
,
1
,
2
,
…
,
n
−
1
)
y^{(j)}(0_+) \, (j=0,1,2,\dots,{n-1})
y ( j ) ( 0 + ) ( j = 0 , 1 , 2 , … , n − 1 )
初始状态 : 是系统在激励尚未接入的
t
=
0
−
t=0_-
t = 0 −
y
(
j
)
(
0
−
)
y^{(j)}(0_-)
y ( j ) ( 0 − )
y
(
t
)
=
y
z
i
(
t
)
+
y
z
s
(
t
)
y(t) = y_{zi}(t) + y_{zs}(t)
y ( t ) = y z i ( t ) + y z s ( t )
系统的微分方程为
77
y
(
t
)
+
2
d
d
t
y
(
t
)
+
d
2
d
t
2
y
(
t
)
=
f
(
t
)
77 y{\left(t \right)} + 2 \frac{d}{d t} y{\left(t \right)} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = f(t)
7 7 y ( t ) + 2 d t d y ( t ) + d t 2 d 2 y ( t ) = f ( t )
在
t
≥
0
t\geq0
t ≥ 0
f
(
t
)
=
10
sin
(
2
π
t
)
f(t)=10\sin(2\pi t)
f ( t ) = 1 0 sin ( 2 π t )
可得
y
′
′
(
t
)
=
−
77
y
(
t
)
−
2
y
′
(
t
)
+
f
(
t
)
,
t
≥
0
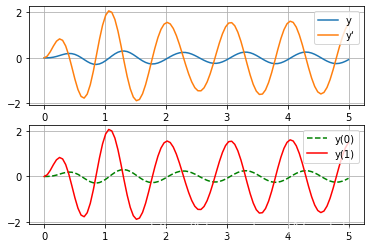
y^{\prime\prime}{\left(t \right)} = - 77 y{\left(t \right)} - 2 y^{\prime}{\left(t \right)} + f(t) , \, t\geq0
y ′ ′ ( t ) = − 7 7 y ( t ) − 2 y ′ ( t ) + f ( t ) , t ≥ 0
from scipy. integrate import odeint, solve_bvp, solve_ivp
def fvdp ( t, y) :
'''
来源:https://www.jianshu.com/p/ab57b600b854?utm_campaign=shakespeare
要把y看出一个向量,y = [dy0,dy1,dy2,...]分别表示y的n阶导
对于二阶微分方程,肯定是由0阶和1阶函数组合而成的,所以下面把y看成向量的话,y0表示最初始的函数,也就是我们要求解的函数,y1表示一阶导,对于高阶微分方程也可以以此类推
'''
y0, y1 = y
ft = 10 * np. sin( 2 * np. pi* t)
y2 = - 2 * y1- 77 * y0+ ft
return [ y1, y2]
y0 = [ 0 , 0 ]
t = np. linspace( 0 , 5 , 100 )
y = odeint( fvdp, y0, t, tfirst= True )
y_ = solve_ivp( fvdp, t_span= ( 0 , 5 ) , y0= y0, t_eval= t)
plt. subplot( 211 )
y1, = plt. plot( t, y[ : , 0 ] , label= 'y' )
y1_, = plt. plot( t, y[ : , 1 ] , label= 'y‘' )
plt. legend( handles= [ y1, y1_] , loc= 'upper right' )
plt. grid( True )
plt. subplot( 212 )
y2, = plt. plot( y_. t, y_. y[ 0 , : ] , 'g--' , label= 'y(0)' )
y2_, = plt. plot( y_. t, y_. y[ 1 , : ] , 'r-' , label= 'y(1)' )
plt. legend( handles= [ y2, y2_] , loc= 'upper right' )
plt. grid( True )
plt. show( )
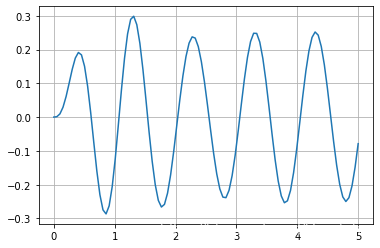
sys = sg. lti( [ 1 ] , [ 1 , 2 , 77 ] )
ft = 10 * np. sin( 2 * np. pi* t)
_, y, _ = sg. lsim( sys, ft, T= t)
plt. plot( t, y, label= 'simple way' )
plt. grid( True )
plt. show( )
由单位冲激函数
δ
(
t
)
\delta(t)
δ ( t )
h
(
t
)
h(t)
h ( t )
δ
(
t
)
→
LTI
→
h
(
t
)
\delta(t) \to \text{LTI} \to h(t)
δ ( t ) → LTI → h ( t ) 隐含条件:
f
(
t
)
=
δ
(
t
)
f(t) = \delta(t)
f ( t ) = δ ( t )
h
(
0
−
)
=
h
′
(
0
−
)
=
0
h(0_-) = h^\prime(0_-) = 0
h ( 0 − ) = h ′ ( 0 − ) = 0
由单位阶跃函数
ε
(
t
)
\varepsilon(t)
ε ( t )
g
(
t
)
g(t)
g ( t )
ε
(
t
)
→
LTI
→
g
(
t
)
\varepsilon(t) \to \text{LTI} \to g(t)
ε ( t ) → LTI → g ( t ) 隐含条件:
f
(
t
)
=
ε
(
t
)
f(t) = \varepsilon(t)
f ( t ) = ε ( t )
g
(
0
−
)
=
g
′
(
0
−
)
=
0
g(0_-)=g^\prime(0_-)=0
g ( 0 − ) = g ′ ( 0 − ) = 0
关联:
g
(
t
)
=
∫
−
∞
t
h
(
τ
)
d
τ
g(t) = \int^t_{-\infty} h(\tau) d\tau
g ( t ) = ∫ − ∞ t h ( τ ) d τ
h
(
t
)
=
d
d
t
g
(
t
)
h(t) = \frac{d }{d t}g(t)
h ( t ) = d t d g ( t )
求以下系统的冲激响应和阶跃响应:
7
y
′
′
(
t
)
+
4
y
′
(
t
)
+
6
y
(
t
)
=
f
′
(
t
)
+
f
(
t
)
7y^{\prime\prime}(t) + 4y^{\prime}(t) + 6y(t) = f^\prime(t) + f(t)
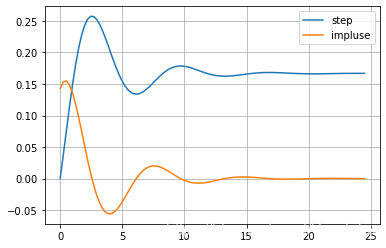
7 y ′ ′ ( t ) + 4 y ′ ( t ) + 6 y ( t ) = f ′ ( t ) + f ( t )
sys = sg. lti( [ 1 , 1 ] , [ 7 , 4 , 6 ] )
st, sy = sg. step2( sys)
it, iy = sg. impulse2( sys)
sy1, = plt. plot( st, sy, label= 'step' )
iy1, = plt. plot( it, iy, label= 'impluse' )
plt. legend( handles= [ sy1, iy1] , loc= 'upper right' )
plt. grid( True )
plt. show( )
来源
f
^
(
t
)
=
∑
n
=
−
∞
∞
f
(
n
Δ
)
Δ
p
(
t
−
n
Δ
)
\hat{f}(t) = \displaystyle\sum_{n=-\infty}^{\infty} f(n\Delta)\Delta p(t-n\Delta)
f ^ ( t ) = n = − ∞ ∑ ∞ f ( n Δ ) Δ p ( t − n Δ )
lim
Δ
→
0
f
^
(
t
)
=
f
(
t
)
=
∫
−
∞
∞
f
(
τ
)
δ
(
t
−
τ
)
d
τ
\lim_{\Delta\to0} \hat{f}(t) = f(t) = \int_{-\infty}^{\infty} f(\tau)\delta(t-\tau)d\tau
Δ → 0 lim f ^ ( t ) = f ( t ) = ∫ − ∞ ∞ f ( τ ) δ ( t − τ ) d τ
由
∫
−
∞
∞
f
(
τ
)
δ
(
t
−
τ
)
d
τ
⟶
∫
−
∞
∞
f
(
τ
)
h
(
t
−
τ
)
d
τ
\int_{-\infty}^{\infty} f(\tau)\delta(t-\tau)d\tau \longrightarrow \int_{-\infty}^{\infty} f(\tau)h(t-\tau)d\tau
∫ − ∞ ∞ f ( τ ) δ ( t − τ ) d τ ⟶ ∫ − ∞ ∞ f ( τ ) h ( t − τ ) d τ
f
(
t
)
→
LTI
→
y
z
s
(
t
)
f(t) \to \text{LTI} \to y_{zs}(t)
f ( t ) → LTI → y z s ( t )
卷积积分
y
z
s
=
∫
−
∞
∞
f
(
τ
)
h
(
t
−
τ
)
d
τ
y_{zs}= \int_{-\infty}^{\infty} f(\tau)h(t-\tau)d\tau
y z s = ∫ − ∞ ∞ f ( τ ) h ( t − τ ) d τ
定义:
f
1
f_1
f 1
f
2
f_2
f 2
f
(
t
)
=
∫
−
∞
∞
f
1
(
τ
)
f
2
(
t
−
τ
)
d
τ
f(t) = \int_{-\infty}^{\infty} f_1(\tau)f_2(t-\tau)d\tau
f ( t ) = ∫ − ∞ ∞ f 1 ( τ ) f 2 ( t − τ ) d τ 记为
f
(
t
)
=
f
1
(
t
)
⋆
f
2
(
t
)
f(t) = f_1(t) \star f_2(t)
f ( t ) = f 1 ( t ) ⋆ f 2 ( t )
代数性质:
三定律:
交换律:
f
1
⋆
f
2
=
f
2
⋆
f
1
f_1 \star f_2 = f_2 \star f_1
f 1 ⋆ f 2 = f 2 ⋆ f 1
分配律:
f
1
⋆
[
f
2
+
f
3
]
=
f
1
⋆
f
2
+
f
1
⋆
f
3
f_1 \star [f_2 + f_3] = f_1\star f_2 + f_1 \star f_3
f 1 ⋆ [ f 2 + f 3 ] = f 1 ⋆ f 2 + f 1 ⋆ f 3
结合律:
[
f
1
⋆
f
2
]
⋆
f
3
=
f
1
⋆
[
f
2
⋆
f
3
]
[f_1\star f_2]\star f_3 = f_1\star [f_2 \star f_3]
[ f 1 ⋆ f 2 ] ⋆ f 3 = f 1 ⋆ [ f 2 ⋆ f 3 ]
特性:
f
(
t
)
⋆
δ
(
t
−
t
0
)
=
δ
(
t
−
t
0
)
⋆
f
(
t
)
=
f
(
t
−
t
0
)
f(t)\star\delta(t-t_0) = \delta(t-t_0) \star f(t) = f(t-t_0)
f ( t ) ⋆ δ ( t − t 0 ) = δ ( t − t 0 ) ⋆ f ( t ) = f ( t − t 0 )
f
(
t
)
⋆
δ
(
n
)
(
t
)
=
f
(
n
)
(
t
)
f(t)\star \delta^{(n)}(t) = f^{(n)}(t)
f ( t ) ⋆ δ ( n ) ( t ) = f ( n ) ( t )
f
(
t
)
⋆
ε
(
t
)
=
∫
−
∞
t
f
(
τ
)
d
τ
f(t) \star \varepsilon(t) = \int_{-\infty}^{t} f(\tau)d\tau
f ( t ) ⋆ ε ( t ) = ∫ − ∞ t f ( τ ) d τ
ε
(
t
)
⋆
ε
(
t
)
=
t
⋅
ε
(
t
)
\varepsilon(t) \star \varepsilon(t) = t \cdot \varepsilon(t)
ε ( t ) ⋆ ε ( t ) = t ⋅ ε ( t ) 衍生:
f
(
t
)
=
f
1
(
t
)
⋆
f
2
(
t
)
f(t) = f_1(t)\star f_2(t)
f ( t ) = f 1 ( t ) ⋆ f 2 ( t )
f
(
t
−
t
1
−
t
2
)
=
f
1
(
t
−
t
1
)
⋆
f
2
(
t
−
t
2
)
=
f
1
(
t
−
t
1
−
t
2
)
⋆
f
2
(
t
)
=
f
1
⋆
f
2
(
t
−
t
1
−
t
2
)
f(t-t_1-t_2) = f_1(t-t_1)\star f_2(t-t_2) = f_1(t-t_1-t_2)\star f_2(t) = f_1 \star f_2(t-t_1-t_2)
f ( t − t 1 − t 2 ) = f 1 ( t − t 1 ) ⋆ f 2 ( t − t 2 ) = f 1 ( t − t 1 − t 2 ) ⋆ f 2 ( t ) = f 1 ⋆ f 2 ( t − t 1 − t 2 )
微分特性:
d
n
d
t
n
[
f
1
(
t
)
⋆
f
2
(
t
)
]
=
f
1
(
n
)
(
t
)
⋆
f
2
(
t
)
=
f
1
(
t
)
⋆
f
2
(
n
)
(
t
)
\frac{d^n}{d t^n}[f_1(t) \star f_2(t)] = f_1^{(n)}(t) \star f_2(t) = f_1(t) \star f_2^{(n)}(t)
d t n d n [ f 1 ( t ) ⋆ f 2 ( t ) ] = f 1 ( n ) ( t ) ⋆ f 2 ( t ) = f 1 ( t ) ⋆ f 2 ( n ) ( t )
∫
−
∞
t
[
f
1
(
τ
)
⋆
f
2
(
τ
)
]
d
τ
=
[
∫
−
∞
t
f
1
(
τ
)
d
τ
]
⋆
f
2
(
t
)
=
f
1
(
t
)
⋆
[
∫
−
∞
t
f
2
(
τ
)
d
τ
]
\int_{-\infty}^{t}[f_1(\tau) \star f_2(\tau)]d\tau = [\int_{-\infty}^{t}f_1(\tau)d\tau]\star f_2(t) = f_1(t) \star [\int_{-\infty}^{t}f_2(\tau)d\tau]
∫ − ∞ t [ f 1 ( τ ) ⋆ f 2 ( τ ) ] d τ = [ ∫ − ∞ t f 1 ( τ ) d τ ] ⋆ f 2 ( t ) = f 1 ( t ) ⋆ [ ∫ − ∞ t f 2 ( τ ) d τ ] if
f
1
(
−
∞
)
=
0
or
f
2
(
−
1
)
(
∞
)
=
0
,
then
f
1
(
t
)
⋆
f
2
(
t
)
=
f
1
′
(
t
)
⋆
f
2
(
−
1
)
(
t
)
f_1(-\infty) = 0 \, \text{or} \, f_2^{(-1)}(\infty)=0, \, \text{then} \, f_1(t)\star f_2(t) = f_1^\prime(t) \star f_2^{(-1)}(t)
f 1 ( − ∞ ) = 0 or f 2 ( − 1 ) ( ∞ ) = 0 , then f 1 ( t ) ⋆ f 2 ( t ) = f 1 ′ ( t ) ⋆ f 2 ( − 1 ) ( t )
常用公式汇总:
K
⋆
f
(
t
)
=
K
⋅
[
f
(
t
)
净面积
]
K \star f(t) = K \cdot [f(t) \text{净面积}]
K ⋆ f ( t ) = K ⋅ [ f ( t ) 净面积 ]
f
(
t
)
⋆
δ
(
t
)
=
f
(
t
)
f(t) \star \delta(t) = f(t)
f ( t ) ⋆ δ ( t ) = f ( t )
f
(
t
)
⋆
δ
′
(
t
)
=
f
′
(
t
)
⋆
δ
(
t
)
=
f
′
(
t
)
f(t) \star \delta^\prime(t) = f^\prime(t) \star \delta(t) = f^\prime(t)
f ( t ) ⋆ δ ′ ( t ) = f ′ ( t ) ⋆ δ ( t ) = f ′ ( t )
f
(
t
)
⋆
ε
(
t
)
=
f
(
t
)
⋆
δ
(
−
1
)
(
t
)
=
f
(
−
1
)
(
t
)
⋆
δ
(
t
)
=
f
(
−
1
)
(
t
)
f(t) \star \varepsilon(t) = f(t) \star \delta^{(-1)} (t) = f^{(-1)}(t) \star \delta(t) = f^{(-1)}(t)
f ( t ) ⋆ ε ( t ) = f ( t ) ⋆ δ ( − 1 ) ( t ) = f ( − 1 ) ( t ) ⋆ δ ( t ) = f ( − 1 ) ( t )
ε
(
t
)
⋆
ε
(
t
)
=
t
⋅
ε
(
t
)
\varepsilon(t) \star \varepsilon(t) = t \cdot \varepsilon(t)
ε ( t ) ⋆ ε ( t ) = t ⋅ ε ( t )
e
−
α
t
ε
(
t
)
⋆
e
−
α
t
ε
(
t
)
=
t
⋅
e
−
α
t
ε
(
t
)
e^{-\alpha t}\varepsilon(t) \star e^{-\alpha t}\varepsilon(t) = t\cdot e^{-\alpha t}\varepsilon(t)
e − α t ε ( t ) ⋆ e − α t ε ( t ) = t ⋅ e − α t ε ( t )
e
−
α
1
t
ε
(
t
)
⋆
e
−
α
2
t
ε
(
t
)
=
1
α
2
−
α
1
(
e
−
α
1
t
−
e
−
α
2
t
)
ε
(
t
)
(
α
1
≠
α
2
)
e^{-\alpha_1 t}\varepsilon(t) \star e^{-\alpha_2 t}\varepsilon(t) =\displaystyle\frac{1}{\alpha_2 - \alpha_1}(e^{-\alpha_1 t} - e^{-\alpha_2 t})\varepsilon(t) \, (\alpha_1 \neq \alpha_2)
e − α 1 t ε ( t ) ⋆ e − α 2 t ε ( t ) = α 2 − α 1 1 ( e − α 1 t − e − α 2 t ) ε ( t ) ( α 1 = α 2 )
ε
(
t
)
⋆
e
−
α
t
ε
(
t
)
=
1
α
(
1
−
e
−
α
t
)
ε
(
t
)
\varepsilon(t) \star e^{-\alpha t}\varepsilon(t) = \frac{1}{\alpha} (1-e^{-\alpha t})\varepsilon(t)
ε ( t ) ⋆ e − α t ε ( t ) = α 1 ( 1 − e − α t ) ε ( t )
f
(
t
)
⋆
δ
T
(
t
)
=
f
(
t
)
⋆
∑
m
=
−
∞
∞
δ
(
t
−
m
T
)
=
∑
m
=
−
∞
∞
f
(
t
−
m
T
)
f(t) \star \delta_T (t) = f(t) \star \displaystyle \sum^{\infty}_{m=-\infty} \delta(t-mT) = \sum^{\infty}_{m=-\infty} f(t-mT)
f ( t ) ⋆ δ T ( t ) = f ( t ) ⋆ m = − ∞ ∑ ∞ δ ( t − m T ) = m = − ∞ ∑ ∞ f ( t − m T )
周期为
T
T
T
δ
T
(
t
)
=
∑
m
=
−
∞
∞
δ
(
t
−
m
T
)
\delta_T(t) = \sum^\infty_{m=-\infty} \delta(t-mT)
δ T ( t ) = ∑ m = − ∞ ∞ δ ( t − m T ) 梳状 comb 函数 。
相关函数:
雷达卷积函数:
R
12
(
t
)
=
f
1
(
t
)
⋆
f
2
(
−
t
)
=
∫
−
∞
∞
f
1
(
τ
)
f
2
(
τ
−
t
)
d
τ
=
∫
−
∞
∞
f
1
(
τ
+
t
)
f
2
(
τ
)
d
τ
=
R
21
(
−
t
)
R_{12} (t) = f_1(t) \star f_2(-t) = \int_{-\infty}^{\infty}f_1(\tau)f_2(\tau-t)d\tau = \int_{-\infty}^{\infty}f_1(\tau+t)f_2(\tau)d\tau = R_{21}(-t)
R 1 2 ( t ) = f 1 ( t ) ⋆ f 2 ( − t ) = ∫ − ∞ ∞ f 1 ( τ ) f 2 ( τ − t ) d τ = ∫ − ∞ ∞ f 1 ( τ + t ) f 2 ( τ ) d τ = R 2 1 ( − t )
R
21
(
t
)
=
f
1
(
−
t
)
⋆
f
2
(
t
)
=
∫
−
∞
∞
f
1
(
τ
)
f
2
(
τ
+
t
)
d
τ
=
∫
−
∞
∞
f
1
(
τ
−
t
)
f
2
(
τ
)
d
τ
=
R
12
(
−
t
)
R_{21} (t) = f_1(-t) \star f_2(t) = \int_{-\infty}^{\infty}f_1(\tau)f_2(\tau+t)d\tau = \int_{-\infty}^{\infty}f_1(\tau-t)f_2(\tau)d\tau = R_{12}(-t)
R 2 1 ( t ) = f 1 ( − t ) ⋆ f 2 ( t ) = ∫ − ∞ ∞ f 1 ( τ ) f 2 ( τ + t ) d τ = ∫ − ∞ ∞ f 1 ( τ − t ) f 2 ( τ ) d τ = R 1 2 ( − t )
Normally
R
12
(
τ
)
≠
R
21
(
τ
)
R_{12}(\tau) \neq R_{21}(\tau)
R 1 2 ( τ ) = R 2 1 ( τ )
自相关函数:
R
(
t
)
=
f
(
t
)
⋆
f
(
−
t
)
=
∫
−
∞
∞
f
(
τ
)
f
(
τ
−
t
)
d
τ
=
∫
−
∞
∞
f
(
τ
+
t
)
f
(
τ
)
d
τ
=
R
(
−
t
)
R (t) = f(t) \star f(-t) = \int_{-\infty}^{\infty}f(\tau)f(\tau-t)d\tau = \int_{-\infty}^{\infty}f(\tau+t)f(\tau)d\tau = R(-t)
R ( t ) = f ( t ) ⋆ f ( − t ) = ∫ − ∞ ∞ f ( τ ) f ( τ − t ) d τ = ∫ − ∞ ∞ f ( τ + t ) f ( τ ) d τ = R ( − t )
其他:
多径传输中存在失真问题, 发射机经某些物体反射产生回波 现象,就算是反射信号也被采集。逆系统 进行补偿。
e
(
t
)
→
回波系统
h
(
t
)
→
r
(
t
)
→
逆系统
h
i
(
t
)
→
e
(
t
)
e(t) \to \text{回波系统} h(t) \to r(t) \to \text{逆系统} h_i (t) \to e(t)
e ( t ) → 回波系统 h ( t ) → r ( t ) → 逆系统 h i ( t ) → e ( t )
e
(
t
)
=
e
(
t
)
⋆
δ
(
t
)
e(t) = e(t) \star \delta (t)
e ( t ) = e ( t ) ⋆ δ ( t )
h
(
t
)
⋆
h
i
(
t
)
=
δ
(
t
)
h(t) \star h_i(t) = \delta(t)
h ( t ) ⋆ h i ( t ) = δ ( t )
h
i
(
t
)
h_i(t)
h i ( t ) 解卷积 或 反卷积
自适应滤波器 AF (Adaptive Filter ) 可以根据误差信号调整系数 去对消 噪声信号,使得输出信号趋近于真实信号。
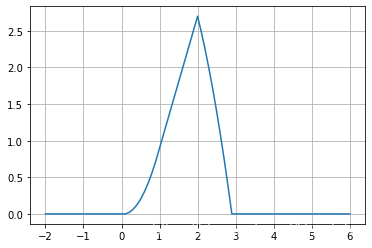
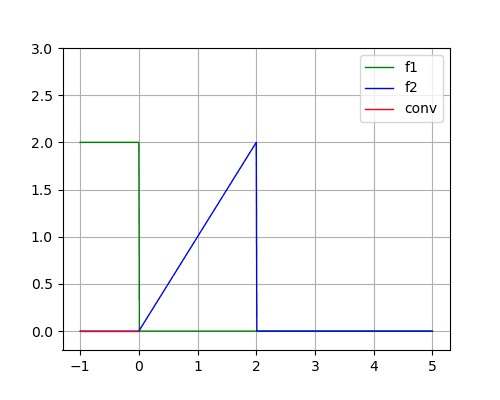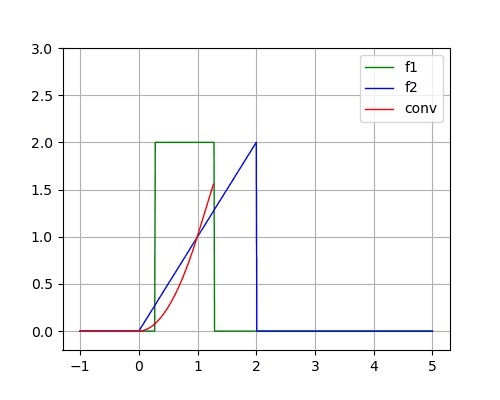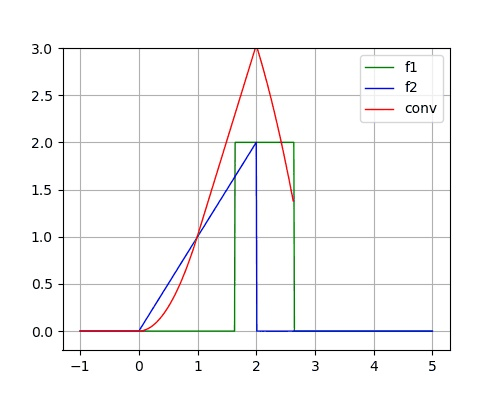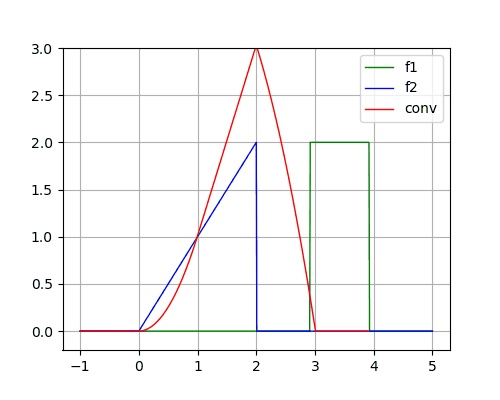
已知两个连续时间信号为:
f
1
(
t
)
=
{
2
,
0
<
t
<
1
0
,
else
f
2
(
t
)
=
{
t
,
0
<
t
<
2
0
,
else
f_1(t) = \begin{cases} 2, \, & 0<t<1 \\ 0, \, & \text{else} \end{cases} \hspace{3em} f_2(t) = \begin{cases} t, \, & 0<t<2 \\ 0, \, & \text{else} \end{cases}
f 1 ( t ) = { 2 , 0 , 0 < t < 1 else f 2 ( t ) = { t , 0 , 0 < t < 2 else
t1 = np. array( [ t* 0.1 for t in range ( - 10 , 31 ) ] )
f1t = np. array( [ 2 if 0 < t< 10 else 0 for t in range ( - 10 , 31 ) ] )
t2 = np. array( [ t* 0.1 for t in range ( - 10 , 31 ) ] )
f2t = np. array( [ t* 0.1 if 0 < t< 20 else 0 for t in range ( - 10 , 31 ) ] )
yt = sg. convolve( f1t, f2t, 'full' ) * 0.1
t3 = np. array( [ t* 0.1 for t in range ( - 20 , 61 ) ] )
plt. plot( t3, yt, label= 'conv' )
plt. grid( True )
plt. show( )
微分算子:
P
=
d
d
t
P = \frac{d}{dt}
P = d t d
P
(
n
)
=
d
n
d
t
n
P^{(n)} = \frac{d^n}{dt^n}
P ( n ) = d t n d n
积分算子:
P
−
1
=
∫
−
∞
t
(
⋅
)
d
τ
P^{-1} = \int^{t}_{-\infty} (\cdot) d\tau
P − 1 = ∫ − ∞ t ( ⋅ ) d τ
性质:
P
P
P 正幂 多项式可以因式分解设
A
(
P
)
,
B
(
P
)
A(P), B(P)
A ( P ) , B ( P )
P
P
P 正幂 多项式,则
A
(
P
)
B
(
P
)
=
B
(
P
)
A
(
P
)
A(P)B(P) = B(P)A(P)
A ( P ) B ( P ) = B ( P ) A ( P )
微分算子方程公因子 不能随意 消去
设
A
(
P
)
,
B
(
P
)
,
D
(
P
)
A(P), B(P), D(P)
A ( P ) , B ( P ) , D ( P )
P
P
P 正幂 多项式,
D
(
P
)
⋅
[
A
(
P
)
D
(
P
)
⋅
B
(
P
)
]
f
(
t
)
=
A
(
P
)
B
(
P
)
f
(
t
)
\displaystyle D(P) \cdot [\frac{A(P)}{D(P)\cdot B(P)}]f(t) = \frac{A(P)}{B(P)}f(t)
D ( P ) ⋅ [ D ( P ) ⋅ B ( P ) A ( P ) ] f ( t ) = B ( P ) A ( P ) f ( t )
A
(
P
)
D
(
P
)
⋅
B
(
P
)
[
D
(
p
)
f
(
t
)
]
≠
A
(
P
)
B
(
P
)
f
(
t
)
\displaystyle\frac{A(P)}{D(P)\cdot B(P)}[D(p)f(t)] \neq \frac{A(P)}{B(P)}f(t)
D ( P ) ⋅ B ( P ) A ( P ) [ D ( p ) f ( t ) ] = B ( P ) A ( P ) f ( t )
传输算子 :
H
(
P
)
=
B
(
P
)
A
(
P
)
=
b
m
P
m
+
b
m
−
1
P
m
−
1
+
⋯
+
b
0
P
n
+
a
n
−
1
P
n
−
1
+
⋯
+
a
0
H(P) = \displaystyle \frac{B(P)}{A(P)} = \frac{b_m P^m+ b_{m-1} P^{m-1} + \dots + b_0}{P^n + a_{n-1}P^{n-1} + \dots + a_0}
H ( P ) = A ( P ) B ( P ) = P n + a n − 1 P n − 1 + ⋯ + a 0 b m P m + b m − 1 P m − 1 + ⋯ + b 0
一阶差分:
一阶前向差分
Δ
f
(
k
)
Δ
k
=
f
(
k
+
1
)
−
f
(
k
)
(
k
+
1
)
−
k
⟶
Δ
f
(
k
)
=
f
(
k
+
1
)
−
f
(
k
)
\text{一阶前向差分}\, \displaystyle \frac{\Delta f(k)}{\Delta k} = \frac{f(k+1)-f(k)}{(k+1)-k} \\ \longrightarrow \Delta f(k) = f(k+1) - f(k)
一阶前向差分 Δ k Δ f ( k ) = ( k + 1 ) − k f ( k + 1 ) − f ( k ) ⟶ Δ f ( k ) = f ( k + 1 ) − f ( k )
一阶后向差分
∇
f
(
k
)
∇
k
=
f
(
k
)
−
f
(
k
−
1
)
k
−
(
k
−
1
)
⟶
∇
f
(
k
)
=
f
(
k
)
−
f
(
k
−
1
)
\text{一阶后向差分}\, \displaystyle \frac{\nabla f(k)}{\nabla k} = \frac{f(k)-f(k-1)}{k-(k-1)} \\ \longrightarrow \nabla f(k) = f(k) - f(k-1)
一阶后向差分 ∇ k ∇ f ( k ) = k − ( k − 1 ) f ( k ) − f ( k − 1 ) ⟶ ∇ f ( k ) = f ( k ) − f ( k − 1 )
线性性质:
∇
[
α
f
1
(
k
)
+
b
f
2
(
k
)
]
=
α
∇
f
1
(
k
)
+
b
∇
f
2
(
k
)
\nabla[\alpha f_1(k) + bf_2(k)] = \alpha \nabla f_1(k) + b\nabla f_2(k)
∇ [ α f 1 ( k ) + b f 2 ( k ) ] = α ∇ f 1 ( k ) + b ∇ f 2 ( k )
二阶差分:
∇
2
f
(
k
)
=
∇
[
∇
f
(
k
)
]
=
f
(
k
)
−
2
f
(
k
−
1
)
+
f
(
k
−
2
)
\nabla^2 f(k) = \nabla[\nabla f(k)] = f(k) - 2f(k-1) + f(k-2)
∇ 2 f ( k ) = ∇ [ ∇ f ( k ) ] = f ( k ) − 2 f ( k − 1 ) + f ( k − 2 )
m阶差分:
∇
m
f
(
k
)
=
f
(
k
)
+
b
1
f
(
k
−
1
)
+
⋯
+
b
m
f
(
k
−
m
)
\nabla^{m} f(k) = f(k) + b_1f(k-1) + \dots + b_mf(k-m)
∇ m f ( k ) = f ( k ) + b 1 f ( k − 1 ) + ⋯ + b m f ( k − m )
差分方程 本质上是 递推的代数方程 , 若已知初始条件和激励, 利用迭代法 可求其数值解。
y
(
k
)
+
a
n
−
1
y
(
k
−
1
)
+
⋯
+
a
0
y
(
k
−
n
)
=
b
m
f
(
k
)
+
b
m
−
1
f
(
k
−
1
)
+
⋯
+
b
0
f
(
k
−
m
)
y(k) + a_{n-1}y(k-1)+\dots + a_0y(k-n) \\ = b_mf(k)+b_{m-1}f^(k-1) + \dots + b_0f(k-m)
y ( k ) + a n − 1 y ( k − 1 ) + ⋯ + a 0 y ( k − n ) = b m f ( k ) + b m − 1 f ( k − 1 ) + ⋯ + b 0 f ( k − m )
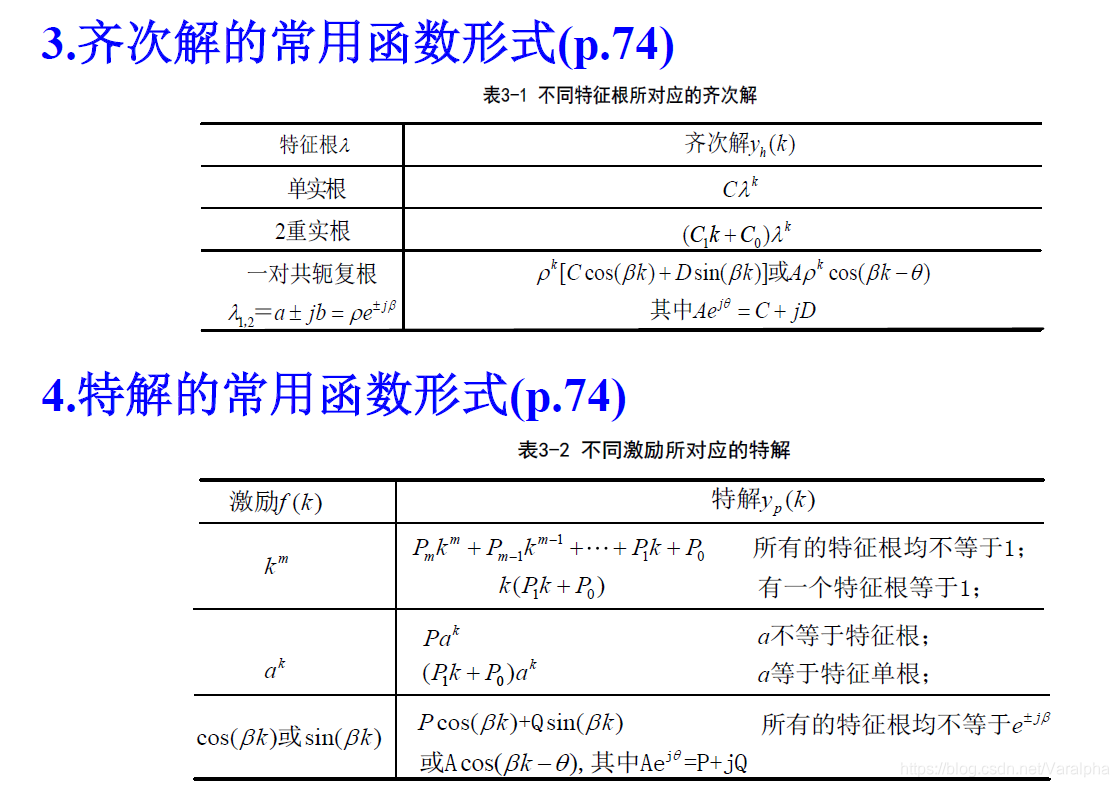
经典解法 :
y
(
k
)
=
y
h
(
k
)
+
y
p
(
k
)
y(k) = y_h(k) + y_p(k)
y ( k ) = y h ( k ) + y p ( k )
y
(
k
)
y(k)
y ( k ) 完全解
y
h
(
k
)
y_h(k)
y h ( k ) 齐次解 homogeneous solution
y
(
k
)
+
a
n
−
1
y
(
k
−
1
)
+
⋯
+
a
0
y
(
k
−
n
)
=
0
y(k) + a_{n-1}y(k-1)+\dots + a_0y(k-n) = 0
y ( k ) + a n − 1 y ( k − 1 ) + ⋯ + a 0 y ( k − n ) = 0
y
p
(
k
)
y_p(k)
y p ( k ) 特解
特征根 : eigenvalue 特征值
1
+
a
n
−
1
λ
−
1
+
⋯
+
a
0
λ
−
n
=
0
→
λ
i
(
i
=
1
,
2
,
…
,
n
)
1 + a_{n-1}\lambda^{-1} + \dots + a_0\lambda^{-n} = 0\, \to\, \lambda_i(i=1,2,\dots, n)
1 + a n − 1 λ − 1 + ⋯ + a 0 λ − n = 0 → λ i ( i = 1 , 2 , … , n )
初始状态 : 用
y
(
−
1
)
,
y
(
−
2
)
,
…
,
y
(
−
n
)
y(-1), y(-2), \dots, y(-n)
y ( − 1 ) , y ( − 2 ) , … , y ( − n )
y
(
−
l
)
=
y
z
i
(
−
l
)
+
y
z
s
(
−
l
)
y(-l) = y_{zi}(-l) + y_{zs}(-l)
y ( − l ) = y z i ( − l ) + y z s ( − l )
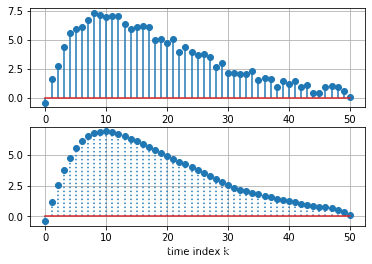
输入信号
f
(
k
)
=
s
(
k
)
+
d
(
k
)
f(k) = s(k) + d(k)
f ( k ) = s ( k ) + d ( k )
s
(
k
)
=
(
2
k
)
0.
9
k
,
d
(
k
)
s(k)= (2k)0.9^k, \, d(k)
s ( k ) = ( 2 k ) 0 . 9 k , d ( k )
M
=
5
M=5
M = 5
y
(
k
)
=
1
M
∑
n
=
0
M
−
1
f
(
k
−
n
)
y(k) = \displaystyle \frac{1}{M}\sum^{M-1}_{n=0}f(k-n)
y ( k ) = M 1 n = 0 ∑ M − 1 f ( k − n )
d = np. random. rand( 1 , 51 ) - 0.5
k = np. array( [ k for k in range ( 0 , 51 ) ] )
s = 2 * k* np. power( 0.9 , k)
f = s+ d[ 0 ]
plt. subplot( 211 )
plt. stem( k, f, '-' , use_line_collection= True )
plt. grid( True )
M = 5
a = 1
b = np. ones( 5 ) / 5
plt. subplot( 212 )
y = sg. filtfilt( b, a, f)
plt. stem( k, y, ':' , use_line_collection= True )
plt. grid( True )
plt. xlabel( 'time index k' )
plt. show( )
单位脉冲序列 (单位样值序列/单位取样序列)
δ
(
k
)
=
{
1
k
=
0
0
k
≠
0
\begin{aligned}\delta(k) = \begin{cases} 1 & k = 0 \\ 0 & k \neq 0\end{cases}\end{aligned}
δ ( k ) = { 1 0 k = 0 k = 0
位移:
δ
(
k
−
k
0
)
=
{
1
k
=
k
0
0
k
≠
k
0
\begin{aligned}\delta(k-k_0) = \begin{cases} 1 & k = k_0 \\ 0 & k \neq k_0\end{cases}\end{aligned}
δ ( k − k 0 ) = { 1 0 k = k 0 k = k 0
加:
δ
(
k
)
+
2
δ
(
k
)
=
3
δ
(
k
)
\delta(k) + 2\delta(k) = 3\delta(k)
δ ( k ) + 2 δ ( k ) = 3 δ ( k )
乘:
δ
(
k
)
⋅
δ
(
k
)
=
δ
(
k
)
\delta(k) \cdot \delta(k) = \delta(k)
δ ( k ) ⋅ δ ( k ) = δ ( k )
延时:
δ
(
k
−
1
)
⋅
δ
(
k
−
2
)
=
0
\delta(k-1) \cdot \delta(k-2) = 0
δ ( k − 1 ) ⋅ δ ( k − 2 ) = 0
迭分:
∑
i
=
−
∞
k
δ
(
i
)
=
{
0
,
k
<
0
1
,
k
≥
0
=
ε
(
k
)
\begin{aligned}\displaystyle \sum^{k}_{i=-\infty} \delta(i) & = \begin{cases} 0, & k<0 \\ 1, & k\geq0 \end{cases} \\ & = \varepsilon(k)\end{aligned}
i = − ∞ ∑ k δ ( i ) = { 0 , 1 , k < 0 k ≥ 0 = ε ( k )
取样性质:
f
(
k
)
δ
(
k
)
=
f
(
0
)
δ
(
k
)
f(k)\delta(k) = f(0) \delta(k)
f ( k ) δ ( k ) = f ( 0 ) δ ( k )
f
(
k
)
δ
(
k
−
k
0
)
=
f
(
k
0
)
δ
(
k
−
k
0
)
f(k)\delta(k-k_0) = f(k_0)\delta(k-k_0)
f ( k ) δ ( k − k 0 ) = f ( k 0 ) δ ( k − k 0 )
∑
k
=
−
∞
∞
δ
(
k
)
=
1
\displaystyle \sum_{k=-\infty}^{\infty} \delta(k) = 1
k = − ∞ ∑ ∞ δ ( k ) = 1
∑
k
=
−
∞
∞
f
(
k
)
δ
(
k
)
=
f
(
0
)
\displaystyle \sum_{k=-\infty}^{\infty} f(k) \delta(k) = f(0)
k = − ∞ ∑ ∞ f ( k ) δ ( k ) = f ( 0 )
∑
k
=
−
∞
∞
f
(
k
)
δ
(
k
−
k
0
)
=
f
(
k
0
)
\displaystyle \sum_{k=-\infty}^{\infty} f(k) \delta(k-k_0) = f(k_0)
k = − ∞ ∑ ∞ f ( k ) δ ( k − k 0 ) = f ( k 0 )
偶函数:
δ
(
k
)
=
δ
(
−
k
)
\delta(k) = \delta(-k)
δ ( k ) = δ ( − k )
单位阶跃序列
ε
(
k
)
=
{
0
k
<
0
1
k
≥
0
\begin{aligned}\varepsilon(k) = \begin{cases} 0 & k < 0 \\ 1 & k \geq 0\end{cases}\end{aligned}
ε ( k ) = { 0 1 k < 0 k ≥ 0
位移:
ε
(
k
−
k
0
)
=
{
0
k
<
k
0
1
k
≥
k
0
\begin{aligned}\varepsilon(k-k_0) = \begin{cases} 0 & k < k_0 \\ 1 & k \geq k_0\end{cases}\end{aligned}
ε ( k − k 0 ) = { 0 1 k < k 0 k ≥ k 0
加:
ε
(
k
)
+
2
ε
(
k
)
=
3
ε
(
k
)
\varepsilon(k) + 2\varepsilon(k) = 3\varepsilon(k)
ε ( k ) + 2 ε ( k ) = 3 ε ( k )
乘:
ε
(
k
)
⋅
ε
(
k
)
=
ε
(
k
)
\varepsilon(k) \cdot \varepsilon(k) = \varepsilon(k)
ε ( k ) ⋅ ε ( k ) = ε ( k )
延时:
ε
(
k
−
1
)
⋅
ε
(
k
−
5
)
=
ε
(
k
−
5
)
\varepsilon(k-1) \cdot \varepsilon(k-5) = \varepsilon(k-5)
ε ( k − 1 ) ⋅ ε ( k − 5 ) = ε ( k − 5 )
迭分:
∑
i
=
−
∞
k
ε
(
i
)
=
{
0
,
k
<
0
k
+
1
,
k
≥
0
=
(
k
+
1
)
ε
(
k
)
\begin{aligned}\displaystyle \sum^{k}_{i=-\infty} \varepsilon(i) & = \begin{cases} 0, & k<0 \\ k+1, & k\geq0 \end{cases} \\ & = (k+1)\varepsilon(k)\end{aligned}
i = − ∞ ∑ k ε ( i ) = { 0 , k + 1 , k < 0 k ≥ 0 = ( k + 1 ) ε ( k )
与
δ
(
k
)
\delta(k)
δ ( k )
δ
(
k
)
=
ε
(
k
)
−
ε
(
k
−
1
)
ε
(
k
)
=
∑
i
=
−
∞
k
δ
(
i
)
\begin{aligned} \delta(k) & = \varepsilon(k) - \varepsilon(k-1) \\ \varepsilon(k) & = \displaystyle \sum_{i=-\infty}^{k}\delta(i) \end{aligned}
δ ( k ) ε ( k ) = ε ( k ) − ε ( k − 1 ) = i = − ∞ ∑ k δ ( i )
由单位脉冲序列
δ
(
k
)
\delta(k)
δ ( k )
h
(
k
)
h(k)
h ( k )
隐含条件:
f
(
k
)
=
δ
(
k
)
f(k) = \delta(k)
f ( k ) = δ ( k )
h
(
−
1
)
=
h
(
−
2
)
=
0
h(-1) = h(-2) = 0
h ( − 1 ) = h ( − 2 ) = 0
由单位阶跃序列
ε
(
k
)
\varepsilon(k)
ε ( k )
g
(
k
)
g(k)
g ( k )
隐含条件:
f
(
k
)
=
ε
(
k
)
f(k) = \varepsilon(k)
f ( k ) = ε ( k )
g
(
−
1
)
=
g
(
−
2
)
=
0
g(-1)=g(-2)=0
g ( − 1 ) = g ( − 2 ) = 0
关联:
g
(
t
)
=
∑
i
=
−
∞
k
h
(
i
)
g(t) = \displaystyle \sum^{k}_{i=-\infty} h(i)
g ( t ) = i = − ∞ ∑ k h ( i )
h
(
t
)
=
∇
g
(
k
)
=
g
(
k
)
−
g
(
k
−
1
)
h(t) = \nabla g(k) = g(k) - g(k-1)
h ( t ) = ∇ g ( k ) = g ( k ) − g ( k − 1 )
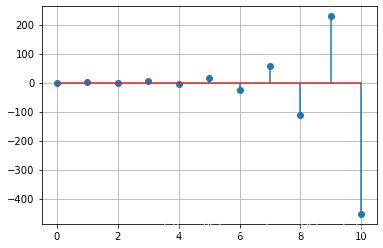
求以下离散系统的单位脉冲响应:
y
(
k
)
+
3
y
(
k
−
1
)
+
2
y
(
k
−
2
)
=
f
(
k
)
y(k) + 3y(k-1) +2y(k-2) = f(k)
y ( k ) + 3 y ( k − 1 ) + 2 y ( k − 2 ) = f ( k )
k = np. array( [ k for k in range ( 11 ) ] )
a = [ 1 . , 3 . , 2 . ]
b = [ 1 . ]
h = sg. lfilter( b, a, k)
plt. stem( k, h, '-' , use_line_collection = True )
plt. grid( True )
plt. show( )
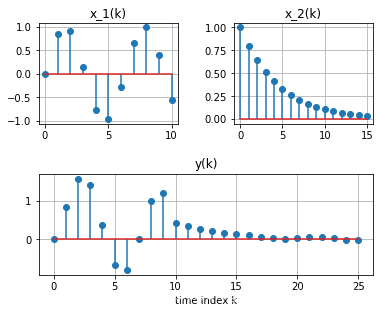
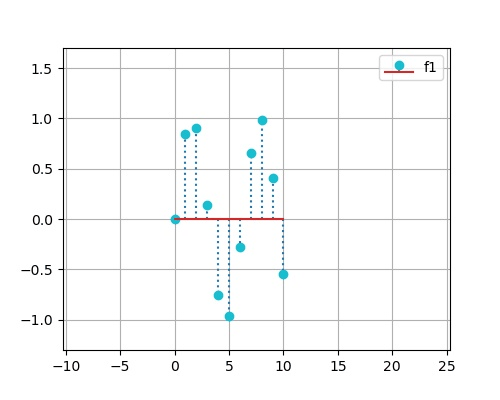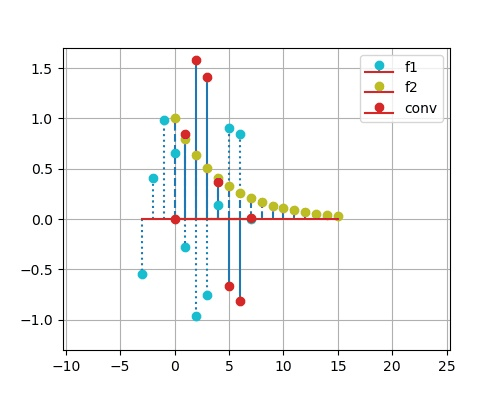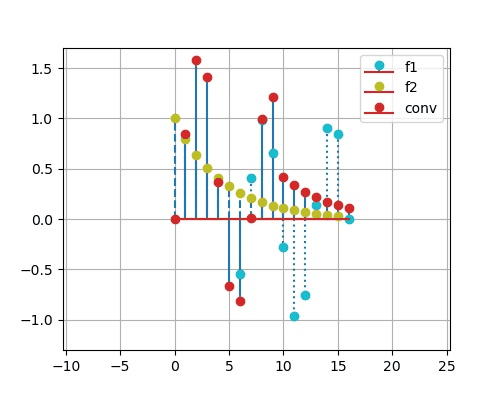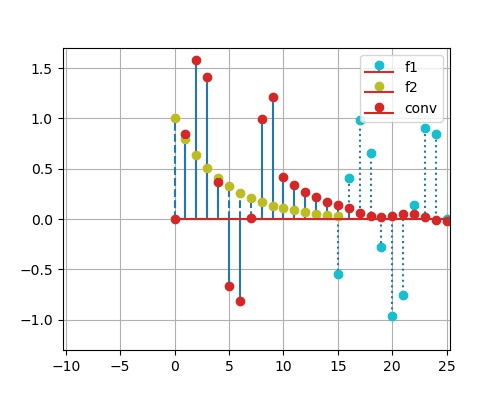
求以下两个离散序列的卷积:
x
1
(
k
)
=
sin
(
k
)
,
0
≤
k
≤
10
x
2
(
k
)
=
0.
8
k
,
0
≤
k
≤
15
x_1(k) = \sin(k),\, 0\leq k \leq 10 \hspace{3em} x_2(k) = 0.8^k,\, 0\leq k\leq 15
x 1 ( k ) = sin ( k ) , 0 ≤ k ≤ 1 0 x 2 ( k ) = 0 . 8 k , 0 ≤ k ≤ 1 5
k1 = np. linspace( 0 , 10 , 11 )
x1 = np. sin( k1)
plt. subplot( 221 )
plt. stem( k1, x1, '-' , use_line_collection= True )
plt. grid( True )
plt. title( 'x_1(k)=sin(k)' )
k2 = np. linspace( 0 , 15 , 16 )
x2 = np. power( 0.8 , k2)
plt. subplot( 222 )
plt. stem( k2, x2, '-' , use_line_collection= True )
plt. grid( True )
plt. title( 'x_2(k) = 0.8^k' )
plt. subplot( 212 )
y = sg. convolve( x1, x2, 'full' )
k3 = np. linspace( 0 , 25 , 26 )
plt. stem( k3, y, '-' , use_line_collection= True )
plt. grid( True )
plt. title( 'y(k)' )
plt. xlabel( 'time index k' )
plt. subplots_adjust( top= 1 , wspace= 0.4 , hspace= 0.5 )
plt. show( )
E
−
1
→
延迟算子
E
→
超前算子
E
−
1
f
(
k
)
=
f
(
k
−
1
)
E
f
(
k
)
=
f
(
k
+
1
)
E
−
2
f
(
k
)
=
f
(
k
−
2
)
E
2
f
(
k
)
=
f
(
k
+
2
)
E
−
n
f
(
k
)
=
f
(
k
−
n
)
E
n
f
(
k
)
=
f
(
k
+
n
)
\begin{aligned} E^{-1} & \to \text{延迟算子} \hspace{3em} & E & \to \text{超前算子} \\ E^{-1}f(k) & = f(k-1) & Ef(k) & = f(k+1) \\ E^{-2}f(k) & = f(k-2) & E^{2}f(k) & = f(k+2) \\ E^{-n}f(k) & = f(k-n) & E^{n}f(k) & = f(k+n)\end{aligned}
E − 1 E − 1 f ( k ) E − 2 f ( k ) E − n f ( k ) → 延迟算子 = f ( k − 1 ) = f ( k − 2 ) = f ( k − n ) E E f ( k ) E 2 f ( k ) E n f ( k ) → 超前算子 = f ( k + 1 ) = f ( k + 2 ) = f ( k + n )