信号与系统公式笔记（6）

主要关于第三章，这章非常重要。
重点内容
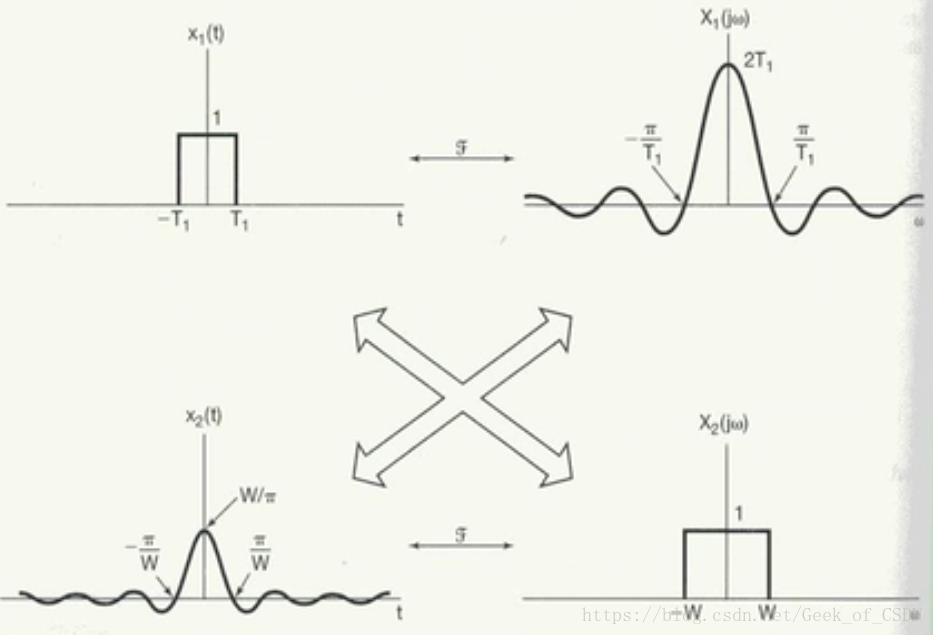
1. 傅里叶级数（至少记住周期矩形脉冲，最好记住周期三角波和锯齿波）
2. 傅里叶变换的定义式、求信号的傅里叶变换、能用傅里叶变换的性质求傅里叶变换（最大的作用就是用来求傅里叶变换）、周期信号的傅里叶变换（用$\sigma(\omega)$）、傅里叶级数和傅里叶变换的转换
3. 系统的频率响应和系统的频域分析
4. 采样定理（其实是傅里叶变换的应用，要很清楚，证明过程也要清楚）

---

信号的带宽
1.$X(\omega)$（频谱）下降到最大值的$\frac{1}{\sqrt{2}}$时对应的频率范围，此时带内信号分量占有信号总能量的$\frac{1}{2}$
2.对包络式$\mathrm{Sa}(x)$形状的频谱，通常定义主瓣宽度（即频谱第一个零点内的范围）为信号带宽

脉宽乘以带宽等于常数$C$（脉宽带宽积）（频域和时域的相反关系）。

---

连续时间傅里叶变换的性质（有时用定义直接积分求不了或者很难求结果，所以只能够用这些性质来简化方程式）
1.线性

$$\mathrm{若}x(t) \leftrightarrow X(\mathrm{j\omega}), y(t) \leftrightarrow Y(\mathrm{j}\omega)\\ \mathrm{则}ax(t) + by(t) \leftrightarrow aX(\mathrm{j}\omega) + bY(\mathrm{j}\omega)$$ 同时也体现了齐次性和可加性

2.时移与频移（必须要记得，很重要）
若$x(t) \leftrightarrow X(\mathrm{j}\omega)$则$x(t - t_0) \leftrightarrow X(\mathrm{j}\omega)\mathrm{e}^{-\mathrm{j}\omega t_0}$
信号的时移只影响它的相频特性，其相频特性会增加一个线性相移。
而频移：

$$F[x(t)\mathrm{e}^{-/+\mathrm{j}\omega t}] = X(\omega+/-\omega_0)$$ （时间上进行变化，会出现频域上的平移）

3.共轭对称性（用起来比较复杂）
若$x(t)\leftrightarrow X(\mathrm{j}\omega)$
泽$x^*(t)\leftrightarrow X^*(-\mathrm{j}\omega)$
（证明不麻烦，记住就行了）

然后因为$X(-\mathrm{j}\omega) = X^*(\mathrm{j}\omega)$所以$X(\mathrm{j}\omega) = X^*(\mathrm{j}\omega)$，所以$X(\mathrm{j}\omega)$是实函数。
所以上面ppt里面的表明是指：“实偶信号的傅里叶变换是实偶函数”（因为是实的所以能够满足了上上面那里的共轭关系）。

如果$x(t)$是奇函数的话：

如果信号$x(t)$是实奇的，那么它的频谱是奇的虚的。

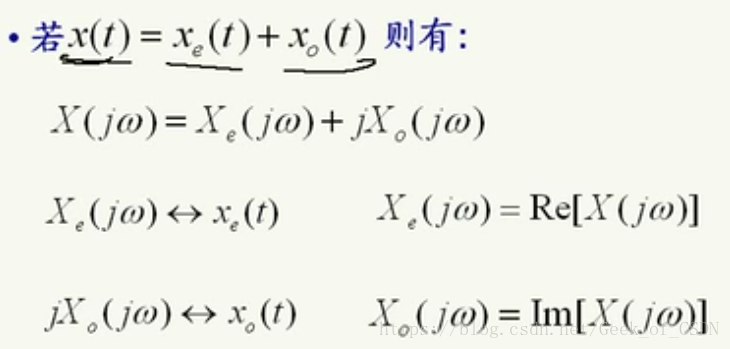
“若”后面的意思是，$x(t)$是一个能用共轭对称和共轭反对称组成的函数。
（知道就行，上面这块比较复杂）

---

下面这题要记住结论

下面在傅里叶变换的时候是先进行傅里叶变换然后进行取极限

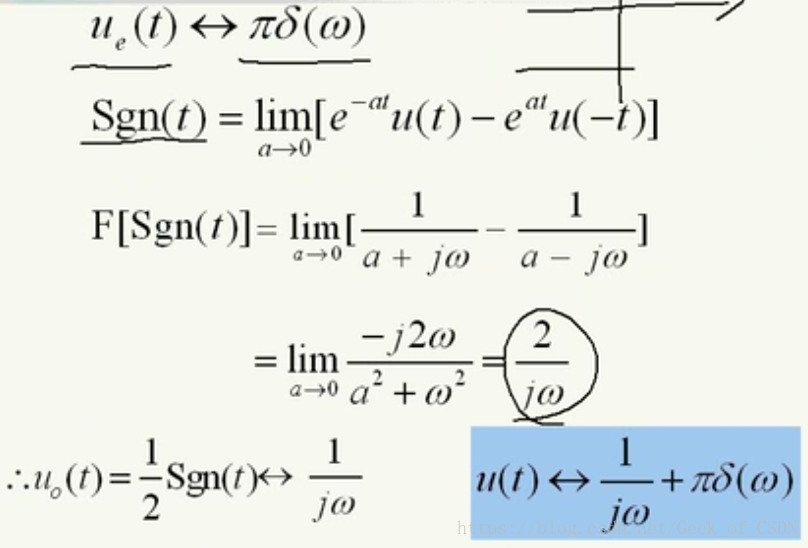
左下角那个$u_o(t)$这样算法其实用了奇函数的性质，$x(t) = \frac{x(t) - x(-t)}{2}$。
过程不用记（因为比较麻烦，直接用傅里叶变换去做做不出来，只能用性质），但是一定要记住左下角的结论，这是阶跃函数的傅里叶变换结果。

---

时域微分与积分
这个性质非常常见，所以要记住啊。
若傅里叶变换是要计算这个$x(t)\leftrightarrow X(\mathrm{j}\omega)$，则$\frac{\mathrm{d}x(t)}{\mathrm{d}t}\leftrightarrow \mathrm{j}\omega X(\mathrm{j}\omega)$（可以将微分运算变成代数运算）
证明比较简单：直接将$x(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty}X(\mathrm{j}\omega)\mathrm{e}^{\mathrm{j}\omega t}\mathrm{d}\omega$两边对$t$微分就可以得到这个性质。
这个性质可以延伸到高次导数，例如$x''(t)\rightarrow(\mathrm{j}\omega)^2X(\mathrm{j}\omega)$

时域积分特性：

$$\int_{-\infty}^{t}x(\tau)\mathrm{d}\tau \leftrightarrow \frac{1}{\mathrm{j}\omega}X(\mathrm{j}\omega) + \pi X(0)\delta(\omega)$$
注意除了除以 $\mathrm{j}\omega$之外还要加上后面那部分。
上面这个结论要记住。

可以从上面这个特性得到$\delta(t)\leftrightarrow 1$和$u(t)\leftrightarrow\frac{1}{\mathrm{j}\omega} + \pi \delta(\omega)$

---

尺度变换

这部分内容可以联想之前的周期矩形脉冲信号和它对应的频谱。

---

对偶性
若$x(t)\leftrightarrow X(\mathrm{j}\omega)$，把右边括号里面的$\omega$换成$t$，就可以得到$X(\mathrm{j}t) \leftrightarrow 2\pi x(-\omega)$。

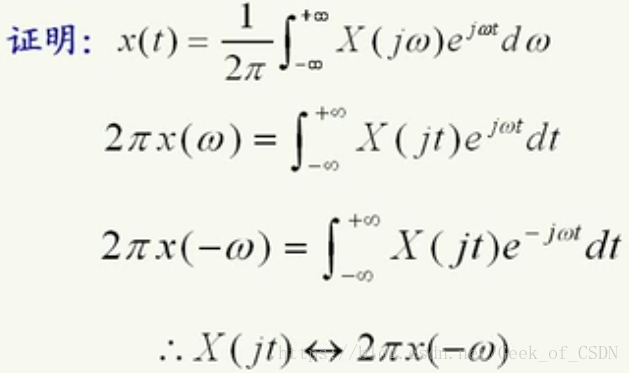
效果大概是这样子的：

然后下面这张图不重要，看看就可以了。

---

频域微积分特性
微分特性
由$X(\mathrm{j}\omega) = \int_{-\infty}^{\infty}x(t)\mathrm{e}^{-\mathrm{j}\omega t}\mathrm{d}t$得$\frac{\mathrm{d}}{\mathrm{d}\omega} X(\mathrm{j}\omega) = \int_{-\infty}^{\infty}-\mathrm{j}tx(t)\mathrm{e}^{-\mathrm{j}\omega t}\mathrm{d}t$（前面其实就是直接对方程两边同时对$\omega$求个导，然后直接把$-\mathrm{j}tx(t)$看作一个整体），所以$-\mathrm{j}tx(t)\leftrightarrow \frac{\mathrm{d}}{\mathrm{d}\omega}X(\mathrm{j}\omega)$（中间那个箭头是指傅里叶变换）
同理，如果是多次求导，那么就是$(-\mathrm{j}t)^n x(t)\leftrightarrow \frac{\mathrm{d}^n}{\mathrm{d}^n\omega}X(\mathrm{j}\omega)$

频域积分特性：（具体证明过程看教材）

$$\int F(\omega) \mathrm{d}\omega = \pi f(0)\delta(t) + \frac{1}{-\mathrm{j}t} f(t)$$
前面那一项是因为积分出现的直流量，积分比。

$(-\mathrm{j}t)^n x(t)\leftrightarrow \frac{\mathrm{d}^n}{\mathrm{d}^n\omega}X(\mathrm{j}\omega)$
和
$\int F(\omega) \mathrm{d}\omega = \pi f(0)\delta(t) + \frac{1}{-\mathrm{j}t} f(t)$
这两条结论要记住，比较重要，公式要记得清楚。

---

时域卷积定理
所有傅里叶性质里面最重要和最常用的一个定理。

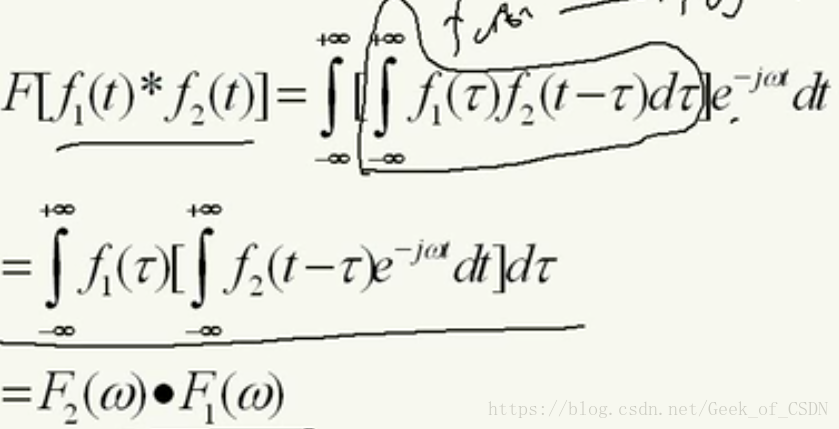
上面这个证明只要看看就行，不用怎么管。

其实结论就是：两个函数卷积的傅里叶变换等于其中每个傅里叶变换的乘积。

经常这么用：

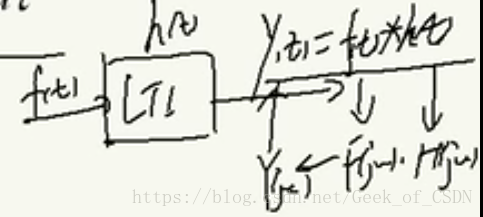
就是将函数输入进去一个LTI系统的时候通常会直接对要进行的卷积进行傅里叶变换，变成两个函数对应的傅里叶变换之后的结果进行的乘积，最后把这个得到的乘积进行傅里叶逆变换得到系统输出。

---

频域卷积定理
下面的这个结论用了频域与时域对称的性质。
箭头指的是傅里叶变换。
若$x_1(t) \leftrightarrow X_1(\mathrm{j}\omega)\quad x_2(t)\leftrightarrow X_2(\mathrm{j}\omega)$
则$x_1(t) \cdot x_2(t) \leftrightarrow \frac{1}{2\pi}X_1(\mathrm{j}\omega) * X_2(\mathrm{j}\omega)$

---

Parseval定理
相当于信号的能量守恒定理。

结论知道就行

---

3.9周期信号的傅里叶变换
周期信号不满足Dirichlet条件（因为不是绝对可积），所以无法直接进行傅里叶变换（虽然可以用傅里叶级数来表示）。

记住：

$$x(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty}X(\mathrm{j}\omega)\mathrm{e}^{\mathrm{j}\omega t}\mathrm{d}\omega = \int_{-\infty}^{\infty}\delta(\omega - \omega_0)\mathrm{e}^{\mathrm{j}\omega t}\mathrm{d}\omega = \mathrm{e}^{\mathrm{j}\omega_0 t}$$

（记得$\mathrm{e}^{\mathrm{j\omega_0}}\rightarrow2\pi\delta(\omega-\omega_0)$
可以这么记：
$1\rightarrow 2\pi\delta(\omega)$
所以$1 \cdot \mathrm{e}^{\mathrm{j}\omega t}\rightarrow 2\pi \delta(\omega - \omega_0$因为产生了频域上的平移。）

所以：周期性复指数信号的频谱是个冲激。

若$x(t) = \mathrm{e}^{\mathrm{j}k\omega_0 t}$则$X(\mathrm{j}\omega) = 2\pi \delta(\omega-k\omega_0$
因为周期信号对应的傅里叶级数是：

$$x(t) = \sum_{k = -\infty}^{\infty}a_k\mathrm{e}^{\mathrm{j}k\omega_0 t}$$
所以周期信号的傅里叶变换表示就是：
$$X(\mathrm{j}\omega) = 2\pi \sum_{k = -\infty}^{\infty}a_k\delta(\omega - k\omega_0)$$
上面这个公式才是 重点。下面是个结论，看看就行。

上面的 $a_k$可以直接用级数的方式进行计算，也可以用别的方法（教材里面有）。

例题：

上面这个可以推广到余弦的情况。下面这道题要注意解出$a_k$的方式。

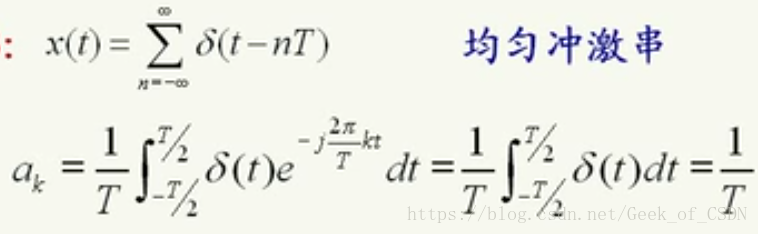
傅里叶级数对应的系数的求法：先求周期信号的主周期的傅里叶变换，然后把变换之后的结果进行取样和用$\frac{1}{T}$调节。

---

3.10 采样定理
有点像ADC（这部分内容没有前两部分内容重要）。

---

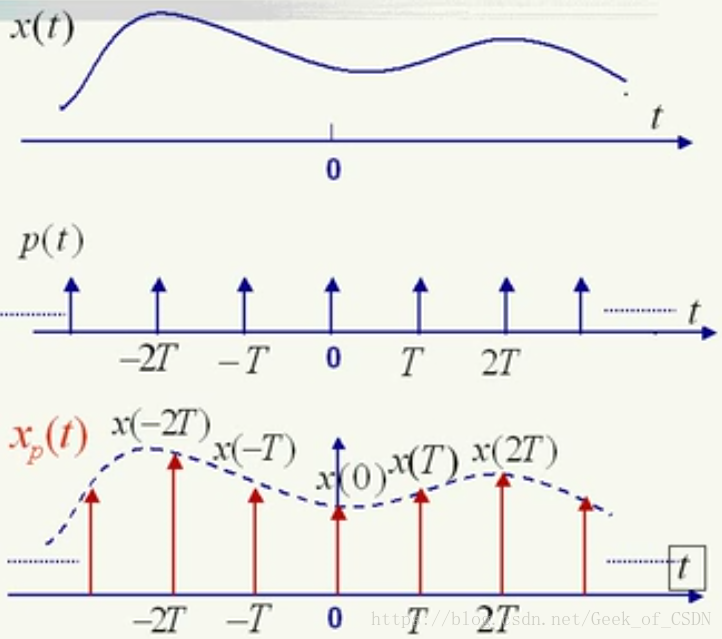
时域采样

采样：在某些离散的时间点上提取连续时间信号值的过程。

采样数学模型

采样结果

对冲激串进行傅里叶变换可以得到另一个系列的冲激串。

效果

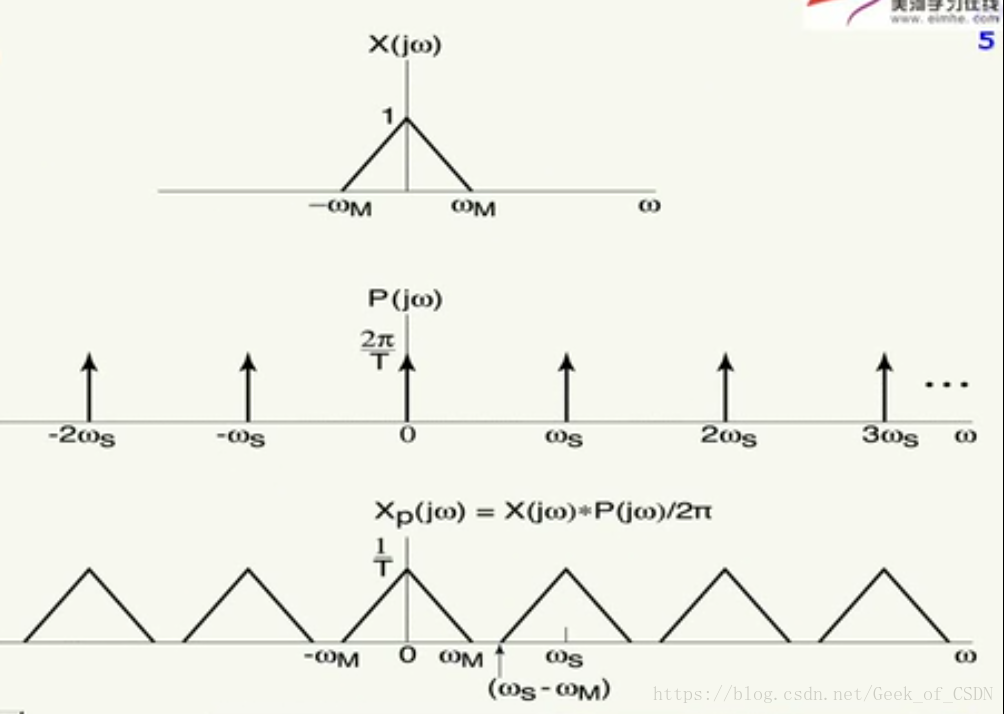
相当于多次平移原信号。

上面图里面提到的带限的其实就是指原信号在横轴上要有界限。

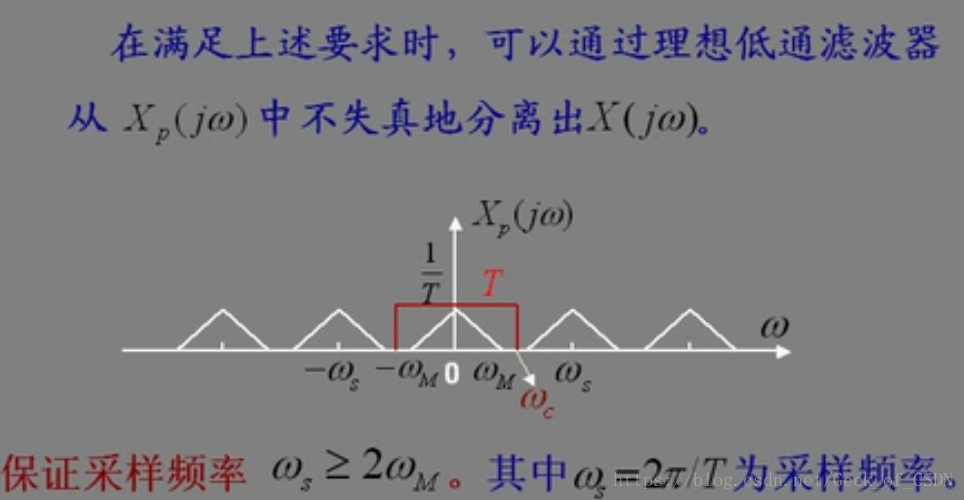
低通滤波起到了图里面红色框的作用，只有红色框里面的信号才可以通过滤波器。（上面的图还暗示了$\omega_M < \omega_C < \omega_S - \omega_M$）

实际上做法

为了补偿采样时频谱幅度的减小，滤波器应具有$T$倍的通带增益。

---

利用内插从样本重建信号

内插：由样本值重建某一函数的过程。也就是用一个连续信号对一组样本值的拟合。重建结果可以是近似的也可以是完全准确的。

带限内插：利用理想低通滤波器的单位冲激响应的内插。

在时间上做卷积是因为之前取样出来的信号是在频域上做乘积的，就是在时域做卷积。上面的$h(t)$在频域的信号是门函数，在时域是取样函数。

用图形看比较形象。

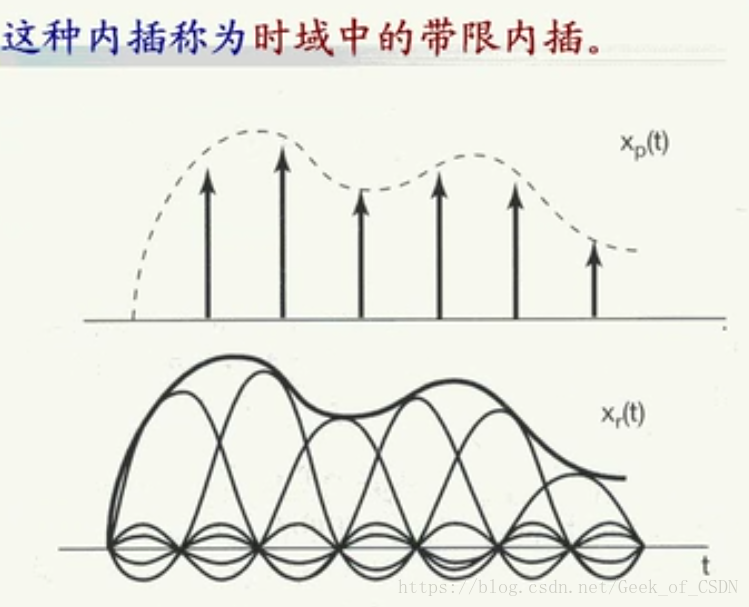
上面就是$X_p(t)$与取样信号分别做卷积，就是把取样信号移动到各个冲激信号对应的点上面，然后就得到$X_r(t)$。