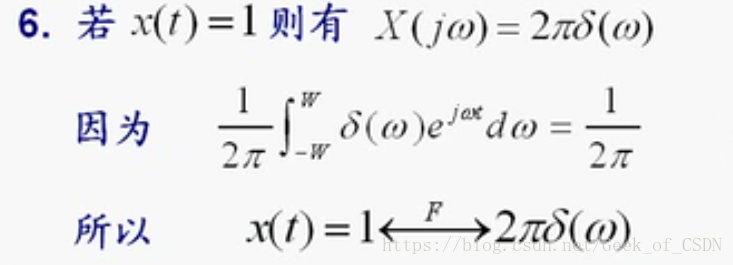重点内容
1.狄利克雷条件
2.Gibbs现象
3.傅里叶变换和傅里叶逆变换公式
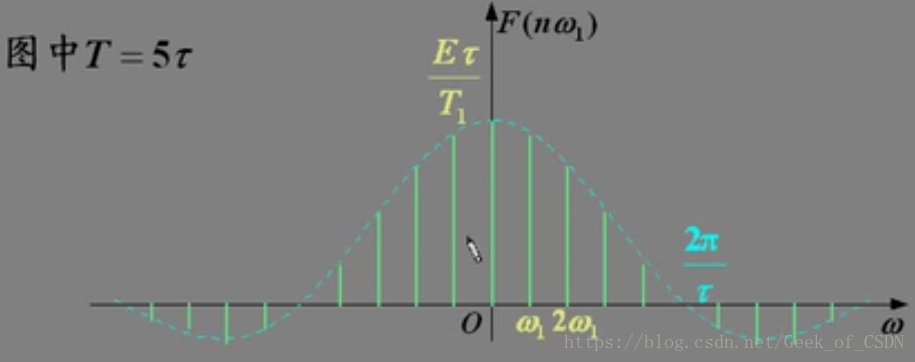
周期矩形脉冲信号
对这个矩形脉冲信号进行积分就可以求到它对应的傅里叶系数

了解一下记得结果就可以了。
补充:
是离散的,只是包络线看起来像是下面这样。
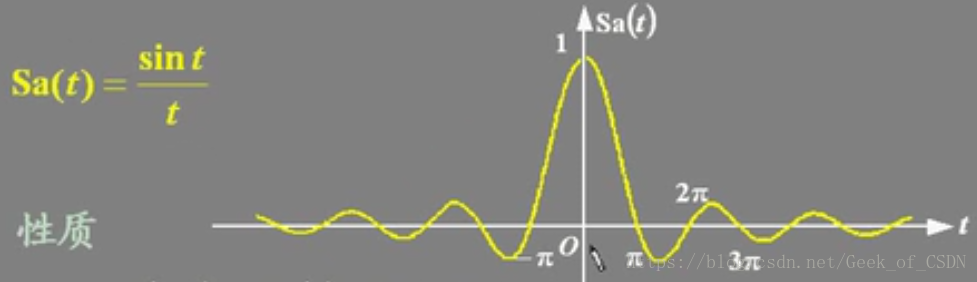
实际上像下面这样
有这些性质要注意:
1.第一个零点坐标:
(令
)
2.
是复函数,幅度/相位
,相位为0,
,相位为
。(我是直接想象成一种类似复指数的那种图形,在负数的时候复指数的初相就相当于在
的位置)
取样信号的零点坐标只与脉冲函数的持续时间有关,而与脉冲函数的周期无关。
上面图里面的两条谱线之间的距离是 ,如果 趋于无穷大,信号会变成非周期信号,那么两条谱线之间的距离会变成无穷小,所以非周期信号的傅里叶谱线会直接变成连续的曲数,而不是像现在这样的离散的曲数。
上图函数的特点:

因为都比较好理解所以直接截图了,懒得特别去记。
补充:上面的
其实就是上上图的谱线的幅度。
频带宽度
定义:在满足一定失真条件下,信号可以用某段频率范围的信号来表示,这段频率范围就是频带宽度。
一般用第一个零点作为频带宽度(因为这里集中了信号的大部分能量),记为:
(其实就是第一个零点的坐标)或
(其实就是除了个
),带宽与脉宽(
)成反比(脉宽太短,那么带宽就会越大,所以通信速率不能无限提高,而要保证信号不失真,就要保证系统的通频带
信号的带宽,有点类似模电里面的放大电路)。
周期信号必须要满足一定的(两组)条件才能够表示成傅里叶级数。
首先是平方可积条件:
如果
则
必存在。因为
,所以一定存在。(其实证明下面的绝对可积就可以了,因为绝对可积要求更加苛刻)
然后主要是狄利克雷条件:
1.
,在任何周期内信号绝对可积(比平方可积条件更加苛刻,所以只要证明绝对可积就可以了)。
因为
这样就可以保证 存在(这个条件往往最苛刻,因为 a > 0$的时候会直接趋于无穷,很多常见信号直接就不能做傅里叶变换了。这个条件存在而让可以用傅里叶变换的地方大大减少)
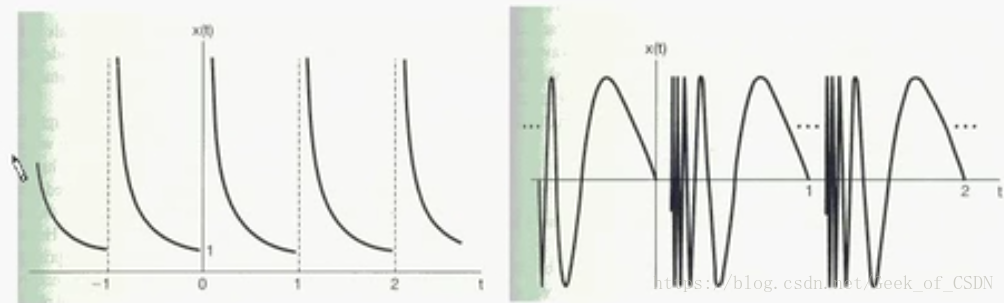
2.在任何有限区间内,只有有限个极值点,且极值为有限值
例如下面这两个信号就不能傅里叶变换
3.在任何有限区间内,只有有限个第一类间断点(就是可去间断点)
Gibbs现象
当满足狄利克雷条件的信号
,当傅里叶级数逼近间断点的时候,如何收敛于
?
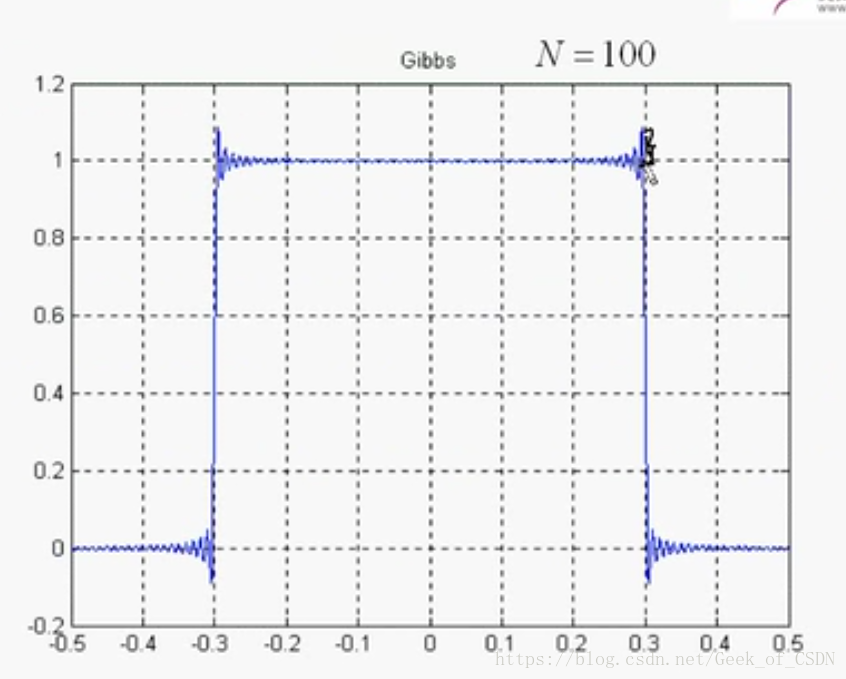
在间断点处的跳变值约等于跳跃间断点的值的
(且跳变值不会因为取得项越多而减少,而是趋于前面那样算出来的值)。
在实际应用中,只会用傅里叶级数的N个项,所以会出现误差(
),然后就可以得出均方误差(下面这个图,了解就可以了)。
在均方误差最小的准则下,傅里叶级数是对周期信号的最佳近似。
傅里叶级数到傅里叶变换
周期
增大时,频谱的幅度会下降,而谱线间隔减小(看上面周期矩形脉冲信号对应的频谱图就知道了),但是包络不变。
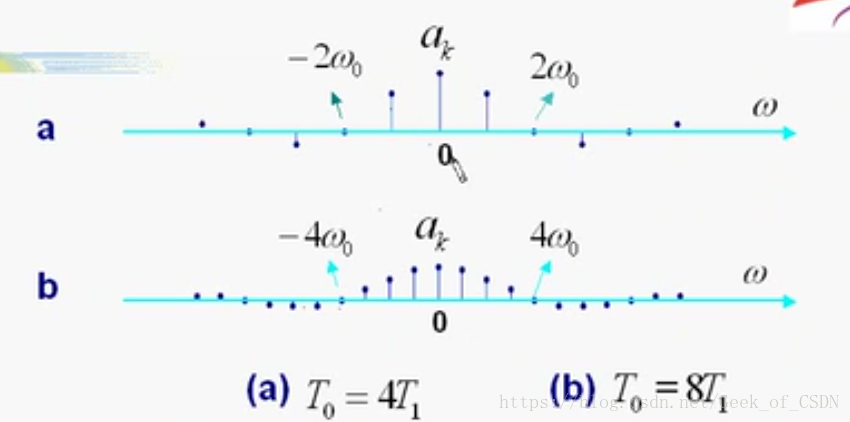
然后是为什么
时频谱会变成连续的:

不用强记,理解就行
上面的推导过程补充:
因为
在
时会直接变成无穷大,所以要乘
变成
来考虑。
继续推导出傅里叶变换和傅里叶逆变换


记不住推导公式没关系,重要的是记住这两个公式:
傅里叶变换用来把信号从时域转到频域,而傅里叶逆变换就是直接反过来把频域转到时域。
上面的东西实在记不住只要记住 是频谱密度函数和那几个公式就行了额,其他的不用管。
一个结论:周期信号的频谱是对应的非周期信号频谱的样本;而非周期信号的频谱是对应的周期信号频谱的包络(还是那个矩形脉冲信号当例子,周期信号的例子就是还是上面那样,非周期信号的例子就是对应的 时的例子)。
傅里叶变化你的收敛
傅里叶变换的收敛条件和傅里叶级数的收敛条件一样,要两组条件:
1.若
则
存在,所以所有能量有限的信号其傅里叶变换一定存在(就是能量信号都有傅里叶变换)。
2.狄利克雷条件
a.
,在任何周期内信号绝对可积(比平方可积条件更加苛刻,所以还是只要证明绝对可积就可以了)。
b.在任何有限区间内,只有有限个极值点,且极值为有限值
c.在任何有限区间内,只有有限个第一类间断点(就是可去间断点)
注意:这些条件只是变换存在的充分条件。
且这两组条件不等价,例如 平方可积,但是不绝对可积。
和周期信号情况一样,当 的傅里叶变换存在时,其傅里叶变换在 的连续处收敛于信号本身,在间断点处收敛于左右极限的平均值,在间断点附近会产生Gibbs现象。
常用信号的傅里叶变换
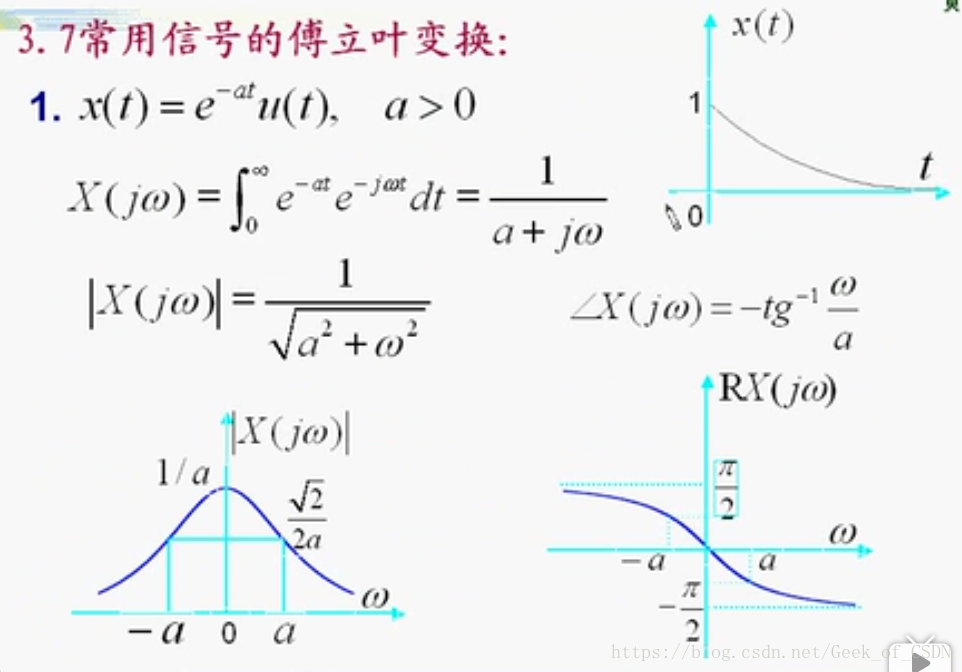
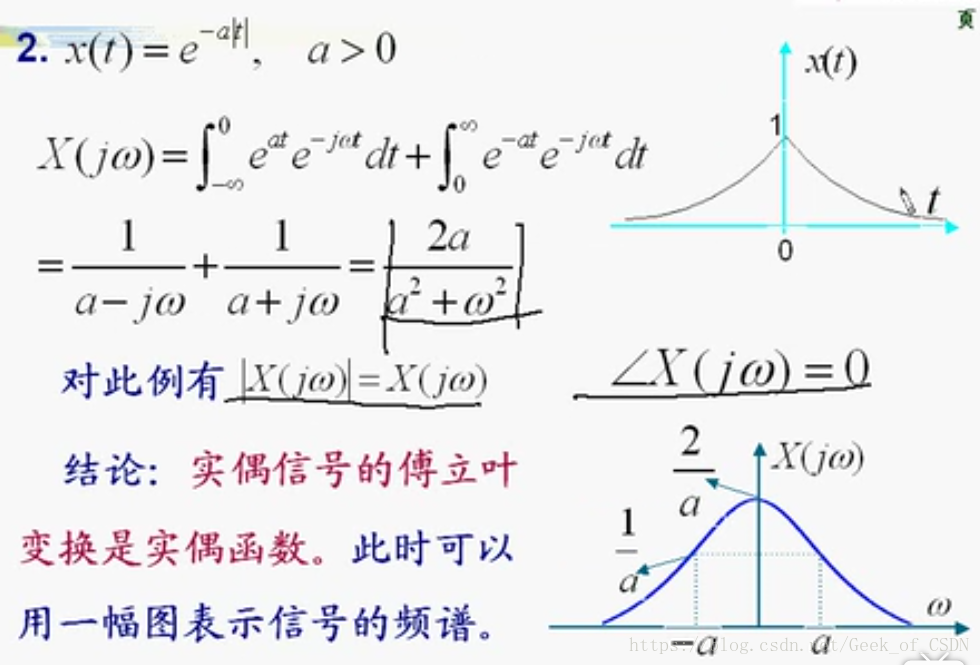

所以冲激函数频谱不满足收敛性,而且可以把信号给分解了(主要是用在求冲激响应那里,冲激响应可以用来和输入信号进行卷积,来求出方程在某些输入信号下对应产生的输出)。

其实就是门函数。
然后就可以得到下面这个结论:
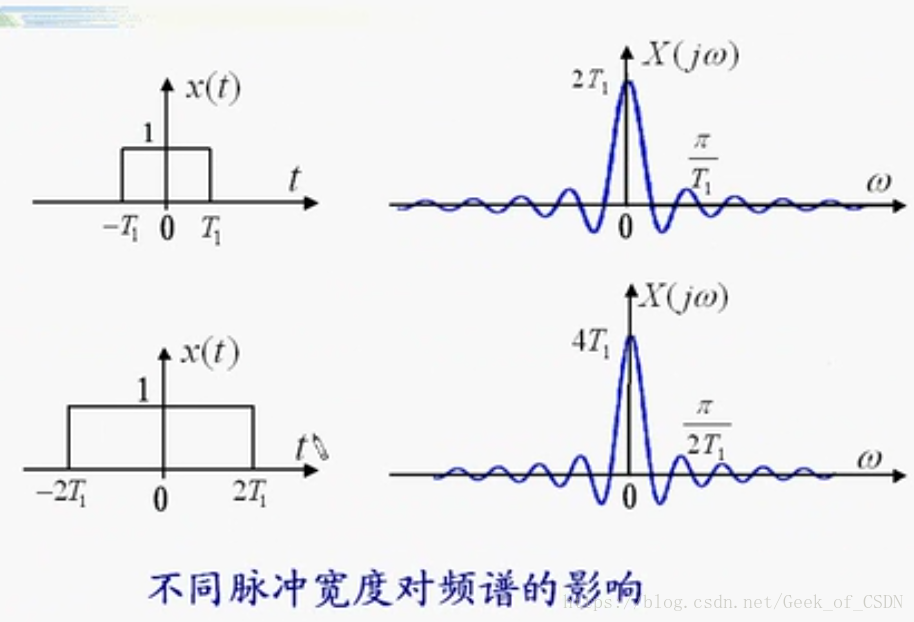
上面图里面的
就是周期信号的周期。记住:门的频谱就是取样函数(强度就是门函数的面积,例如
,上图上面那种就是对应着
)。
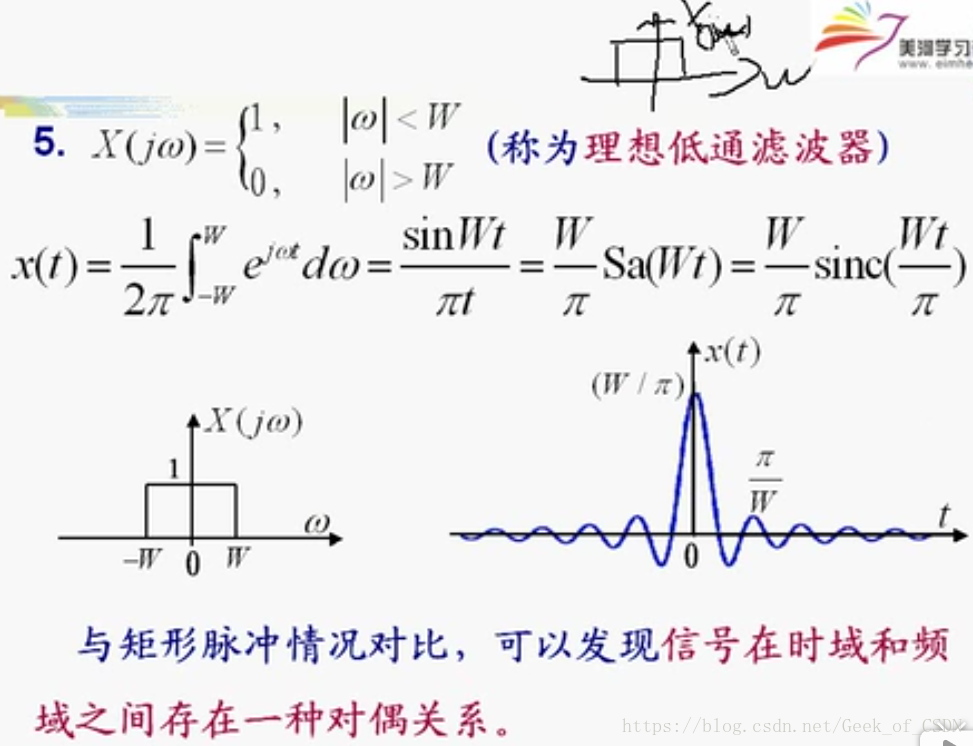
记住这个结论(补充:刚好取样信号对应过去的门的幅度是
)。