Author:AXYZdong
自动化专业 工科男
有一点思考,有一点想法,有一点理性!
一、信号
1、概念
信号:物质的运动形式或状态的变化。
表示:信号常用时间函数(或序列)表示。该函数的图像称为信号的波形。
2、分类
| 分类标准 |
信号类别 |
| 以自变量取值分类 |
连续信号、离散信号 |
| 以信号的起始时刻分类 |
因果信号、非因果信号 |
| 以
f(t)取值分类 |
周期信号、非周期信号 |
| 以确立与随机分类 |
确定信号、随机信号 |
| 以
f(t)为实函数或复函数分类 |
实信号、复信号 |
| 以能量是否有限分类 |
能量有限信号、能量无限信号 |
3、周期信号和非周期信号
3.1、基本概念
周期信号(period signal)是定义在 (-
∞,+
∞)区间,每隔一定时间
T(或整数
N),按相同规律重复变化的信号。
连续周期信号
f(t)满足:
f(t)=f(t+mT),m=0,±1,±2,...
离散周期信号
f(k)满足:
f(k)=f(k+mN),m=0,±1,±2,...
满足上述关系的最小
T(或整数
N)称为该信号的周期。不具有周期性的信号称为非周期信号。
3.2、周期
T求法
举两个例子,通过例子来说明具体求法。
(1)
f1(t)=sin2t+cos3t (2)
f2(t)=cos2t+sinπt
解: 两个周期信号
x(t),y(t)的周期分别为
T1,T2,若其周期之比
T2T1为有理数,则其和信号
x(t)+y(t)仍然是周期信号,其周期为
T1和
T2的最小公倍数。
(1)
sin2t,T1=22π=π
cos3t,T2=32π
T2T1=23为有理数,
f1(t)为周期信号,周期
2π
(2)
cos2t,T1=22π=π
sinπt,T2=π2π=2
T2T1=2π为无理数,
f2(t)为非周期信号
总结:①连续的正弦信号一定是周期信号
②正弦序列不一定是周期序列
③ 两连续周期信号之和不一定是周期信号
④两周期序列之和一定是周期序列
二、系统
1、概念
系统(system):由若干个相互联系、相互作用的单元组成的具有一定功能的整体。
例:收音机系统
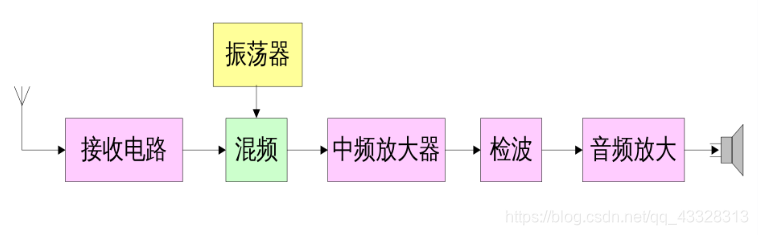
表示:图示、方程(微分方程、差分方程)。
2、分类
按系统处理信号的形式分类
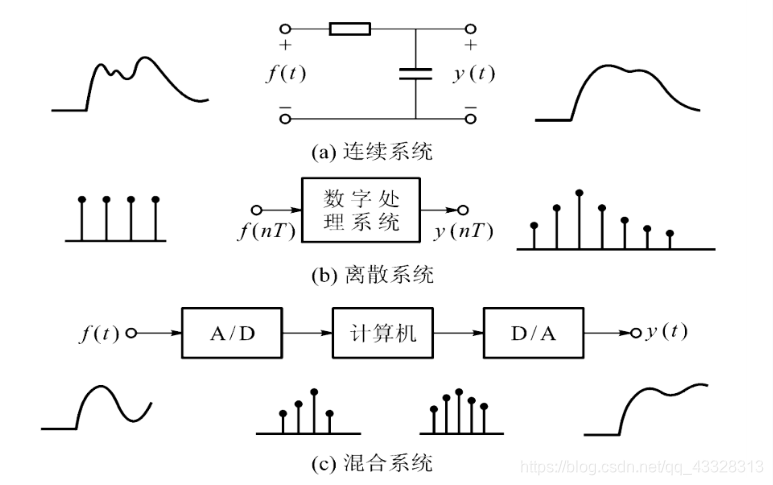
3、线性系统
3.1概念
线性(linearity property):均匀性、叠加性。
线性系统:指具有线性特性的系统
系统的线性特性:
f1(t)
H
y1(t)
f2(t)
H
y2(t)
α1f1(t)+α2f2(t)
H
α1y1(t)+α2y2(t)
3.2线性系统的判断方法
先线性运算,再经系统 = 先经系统,再线性运算
f1(t) C1
C1f1(t)
f2(t) C2
C2f2(t)}→C1f1(t)+C2f2(t)→H→H{C1f1(t)+C2f2(t)}
f1(t) H
H{f1(t)}
f2(t) H
H{f2(t)}}→H{f1(t)}+H{f2(t)}→C→C1H{f1(t)}+C2H{f2(t)}
若
H{C1f1(t)+C2f2(t)}=C1H{f1(t)}+C2H{f2(t)}
则系统
H为线性系统
例:判断方程所描述的系统的线性
y(k)+(k−1)y(k−1)=f(k)
解:
f1(k)→y1(k),f2(k)→y2(k)f1(k)+f2(k)=y1(k)+y2(k)+(k−1){y1(k−1)+y2(k−1)}f1(k)+f2(k)→y1(k)+y2(k)f1(k)+f2(k)=y1(k)+y2(k)+(k−1){y1(k−1)+y2(k−1)}
故:方程所描述的系统是线性系统。
4、时不变系统
4.1概念
时不变系统:一个系统,在零初始条件下,其输出响应与输入信号施加于系统的时间起点无关,这样的系统称为时不变系统。
时不变性:系统具有上述的性质称为时不变性。
4.2判断方法
先时移,再经系统 = 先经系统,再时移
f(t)→时移τ→f(t−τ)→H→H{f(t−τ)}
f(t)H→H{f1(t)}
令y(t)=H{f1(t)}→时移τ→y(t−τ)
若:
H{f(t−τ)}=y(t−τ),则系统
H是时不变系统。
5、线性时不变系统(Linear and Time-invariant System)
线性时不变系统:系统既是线性的,又是时不变的;或系统的方程为线性常系数微分方程。
三、常用的基本信号
1、单位阶跃信号(unit step signal)
ϵ(t)={1,0,t>0t<0
时移
t0
ϵ(t−t0)={1,0,t>t0t<t0
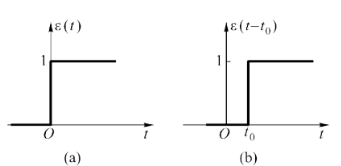
2、矩形脉冲信号(门函数)
gτ(t)={1,0,(∣t∣<2τ)(∣t∣>2τ)
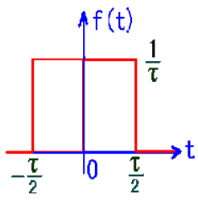
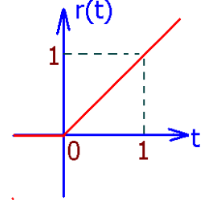
3、斜坡信号(ramp signal)
r(t)={0,t,t<0t≥0
=tϵ(t)
4、取样函数(sampling function)
Sa(t)=tsin(−∞<t<+∞)
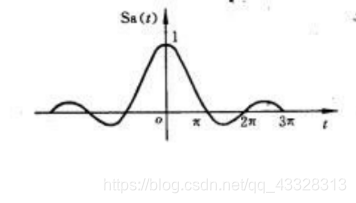
①偶函数
② 当
t=0时,
Sa(t)=1为最大值
③ 曲线呈衰减振荡
④
∫0∞Sa(t)dt=2π,∫∞∞Sa(t)dt=π
取样函数常用形式
sinc(t)=πtsinπt=Sa(πt)
5、单位冲激函数(unit impulse function)
视作矩形脉冲的极限
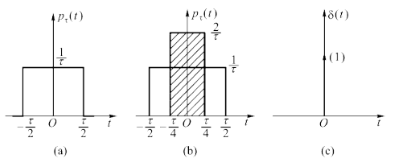
δ(t)={∞,0,t=0t=0
∫∞∞δ(t)dt=1
延时冲激:
Aδ(t−t0)
冲激偶:
δ′(t)=dtdδ(t)
性质:1、偶函数:
δ(t)=δ(−t)
2、取样性:
f(t)⋅δ(t)=f(0)⋅δ(t)f(t)⋅δ(t−t0)=f(t0)⋅δ(t−t0)
∫∞∞f(t)⋅δ(t)dt=f(0)∫∞∞f(t)⋅δ(t−t0)dt=f(t0)
δ(t)与
ϵ(t)的关系:
∫∞tδ(τ)dτ=ϵ(t)
dtdϵ(t)=δ(t)
利用该性质可对不连续函数求导。
码字不易,大家的支持就是我坚持下去的动力。点赞后不要忘了关注我哦!
(PS:写带有数学公式的文章太难了,写完这篇再也不想写了,是第一篇还是最后一篇?就取决于大家的支持啦)







