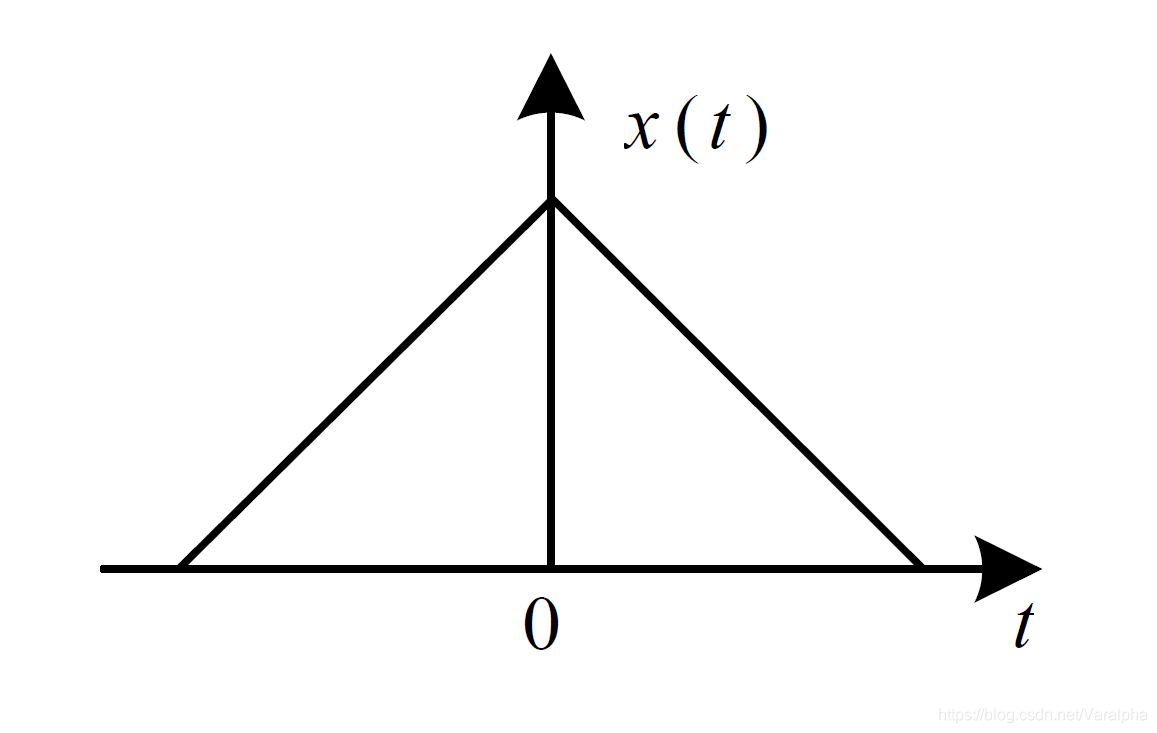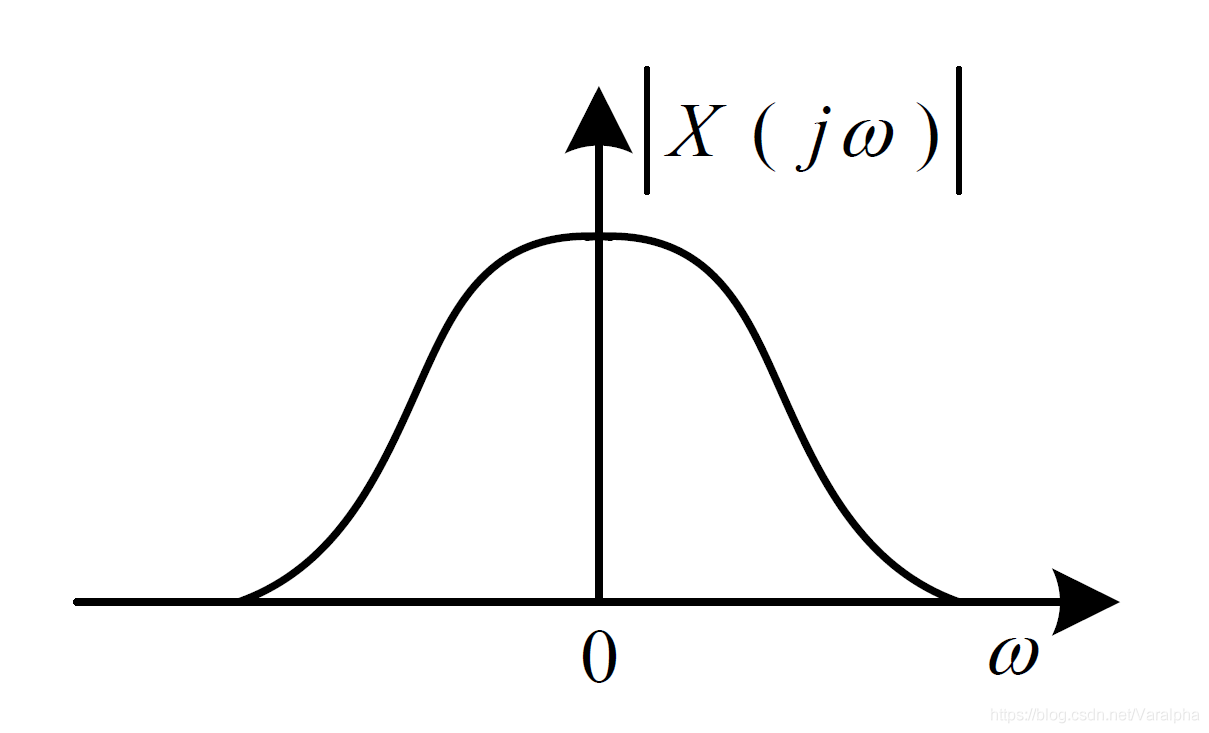变换
时域
时域 特性Time Domain 频域
频域 特性Frequency Domain
傅里叶变换 连续非周期
x
(
t
)
=
1
2
π
∫
−
∞
∞
X
(
j
ω
)
e
j
ω
t
d
ω
\displaystyle x({\color{red}t}) = \frac{1}{2\pi}\int^{\infty}_{-\infty}X(j\omega)e^{j\omega {\color{red}t}}d\omega
x ( t ) = 2 π 1 ∫ − ∞ ∞ X ( j ω ) e j ω t d ω
连续非周期
X
(
j
ω
)
=
∫
−
∞
∞
x
(
t
)
e
−
j
ω
t
d
t
\displaystyle X({\color{red}j\omega}) = \int^{\infty}_{-\infty}x(t)e^{{\color{red}-j\omega} t}dt
X ( j ω ) = ∫ − ∞ ∞ x ( t ) e − j ω t d t
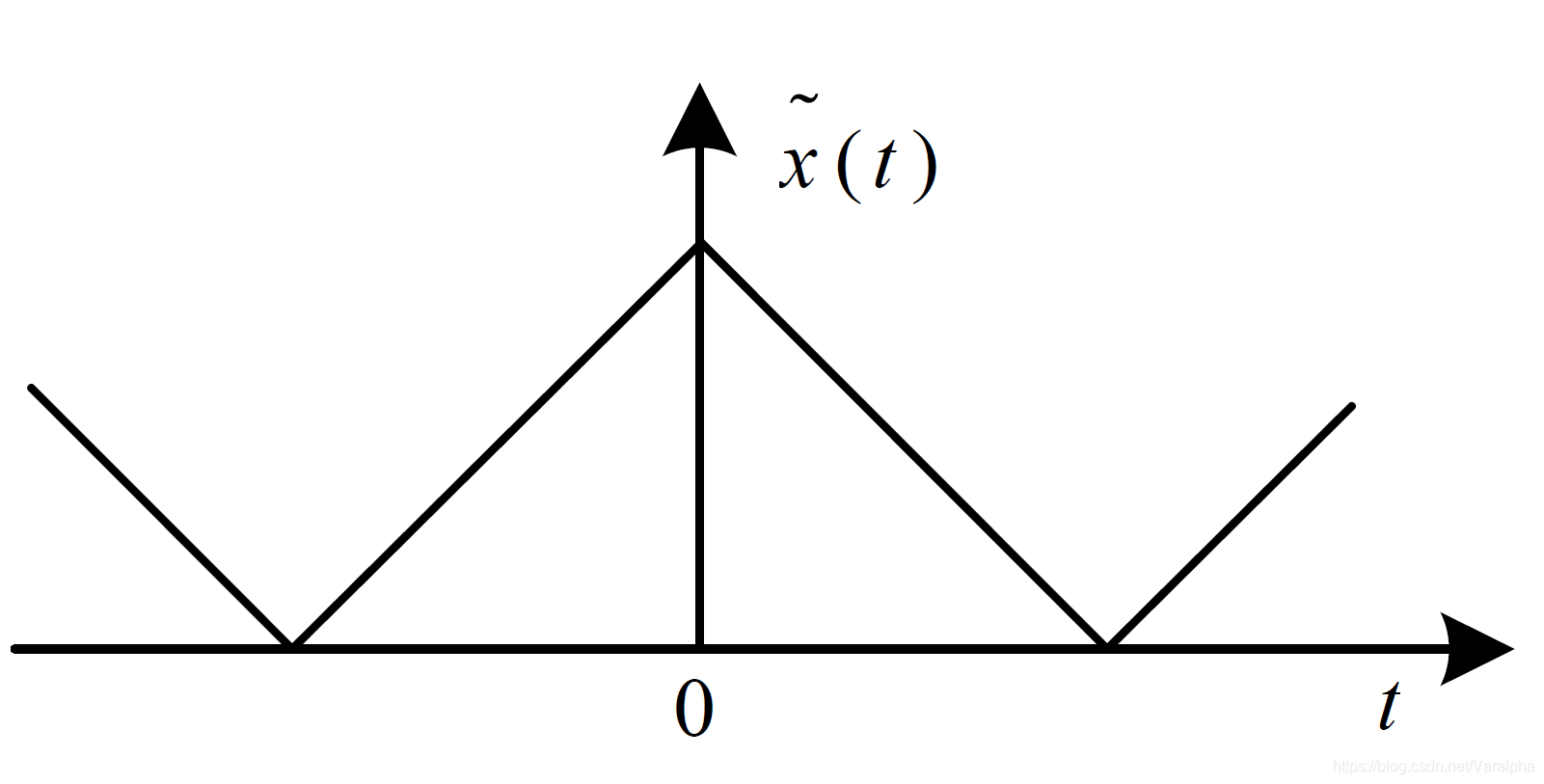
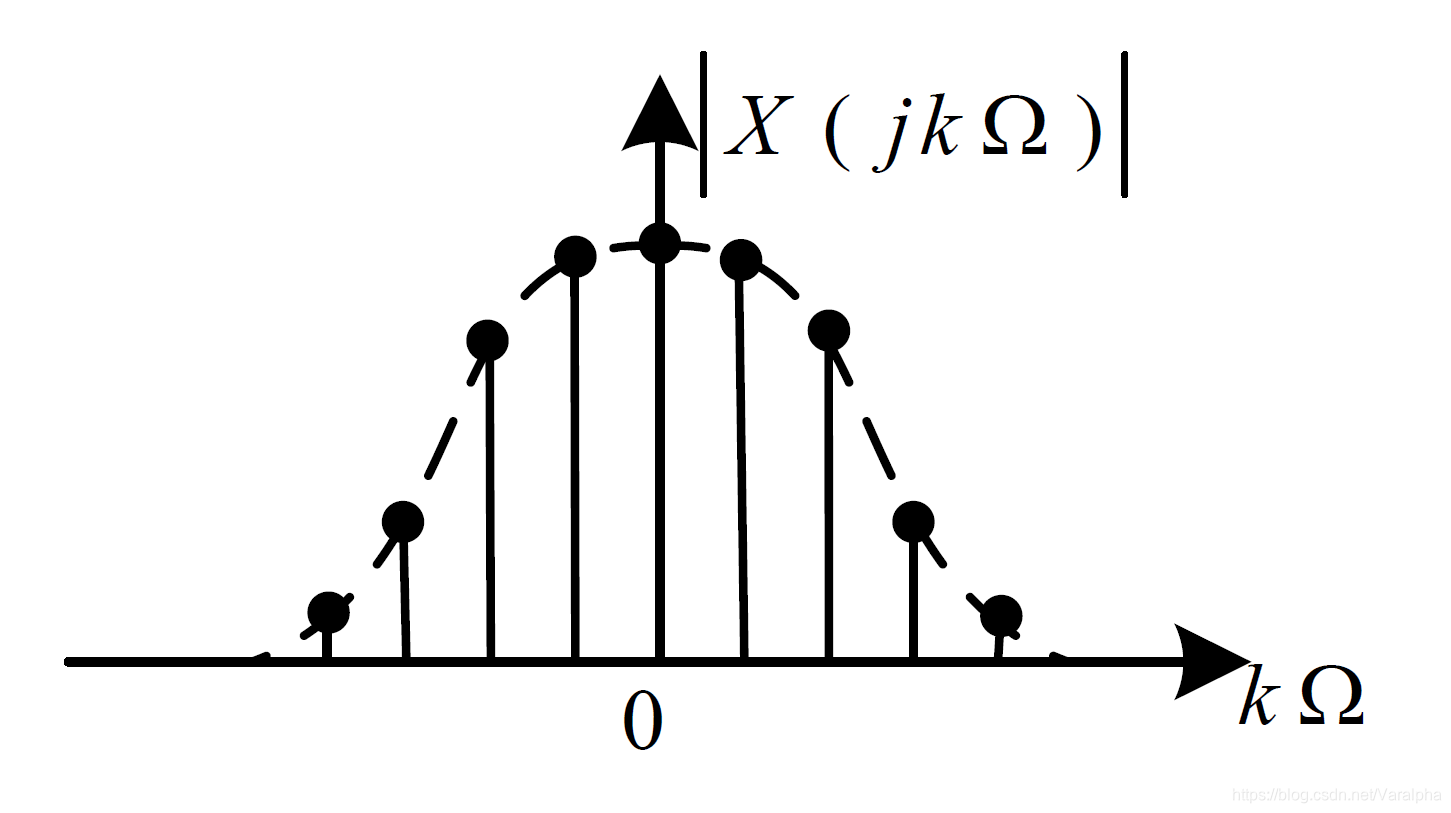
傅里叶级数 连续周期
x
~
(
t
)
=
∑
k
=
−
∞
∞
X
(
j
k
Ω
)
e
j
k
Ω
t
\displaystyle \tilde{x}({\color{red}t}) = \sum^{\infty}_{k = -\infty} X(jk\Omega)e^{jk\Omega {\color{red}t}}
x ~ ( t ) = k = − ∞ ∑ ∞ X ( j k Ω ) e j k Ω t
离散非周期
X
(
j
k
Ω
)
=
1
T
∫
0
T
x
~
(
t
)
e
−
j
k
Ω
t
d
t
\displaystyle X( {\color{red}jk\Omega}) = \frac{1}{T} \int^{T}_{0} \tilde{x}(t) e^{{\color{red}-jk\Omega} t} dt
X ( j k Ω ) = T 1 ∫ 0 T x ~ ( t ) e − j k Ω t d t
离散时间傅里叶变换 离散非周期
x
[
n
]
=
1
2
π
∫
−
π
π
X
(
j
ω
)
e
j
ω
n
d
ω
\displaystyle x[{\color{red}n}] = \frac{1}{2\pi}\int^{\pi}_{-\pi}X(j\omega)e^{j\omega {\color{red}n}}d\omega
x [ n ] = 2 π 1 ∫ − π π X ( j ω ) e j ω n d ω
连续周期
X
(
e
j
ω
)
=
∑
n
=
−
∞
∞
x
[
n
]
e
−
j
ω
n
\displaystyle X(e^{ {\color{red}j\omega}}) = \sum^{\infty}_{n=-\infty} x[n] e^{{\color{red}-j\omega} n}
X ( e j ω ) = n = − ∞ ∑ ∞ x [ n ] e − j ω n
离散傅里叶级数 离散周期
x
~
[
n
]
=
∑
k
=
0
N
−
1
X
~
[
k
]
e
j
2
π
N
k
n
\displaystyle \tilde{x}[{\color{red}n}] = \sum^{N-1}_{k=0} \tilde{X}[k]e^{j\frac{2\pi}{N}k{\color{red}n}}
x ~ [ n ] = k = 0 ∑ N − 1 X ~ [ k ] e j N 2 π k n
−
∞
<
n
<
+
∞
-\infty < {\color{red}n}< +\infty
− ∞ < n < + ∞
离散周期
X
~
[
k
]
=
1
N
∑
n
=
0
N
−
1
x
~
[
n
]
e
−
j
2
π
N
k
n
\displaystyle \tilde{X}[{\color{red}k}] = \frac{1}{N}\sum^{N-1}_{n=0} \tilde{x}[n]e^{ {\color{red}-}j\frac{2\pi}{N}{\color{red}k}n}
X ~ [ k ] = N 1 n = 0 ∑ N − 1 x ~ [ n ] e − j N 2 π k n
−
∞
<
k
<
+
∞
-\infty < {\color{red}k}< +\infty
− ∞ < k < + ∞
离散傅里叶变换 离散非周期
x
[
n
]
=
1
N
∑
k
=
0
N
−
1
X
[
k
]
e
j
2
π
N
k
n
\displaystyle x[{\color{red}n}] = \frac{1}{N} \sum^{N-1}_{k=0} X[k]e^{j\frac{2\pi}{N}k{\color{red}n}}
x [ n ] = N 1 k = 0 ∑ N − 1 X [ k ] e j N 2 π k n
0
<
n
<
N
−
1
0 < {\color{red}n}< N-1
0 < n < N − 1
离散非周期
X
[
k
]
=
∑
n
=
0
N
−
1
x
[
n
]
e
−
j
2
π
N
k
n
\displaystyle X[{\color{red}k}] = \sum^{N-1}_{n=0} x[n]e^{ {\color{red}-}j\frac{2\pi}{N}{\color{red}k}n}
X [ k ] = n = 0 ∑ N − 1 x [ n ] e − j N 2 π k n
0
<
k
<
N
−
1
0 < {\color{red}k}< N-1
0 < k < N − 1
说明:
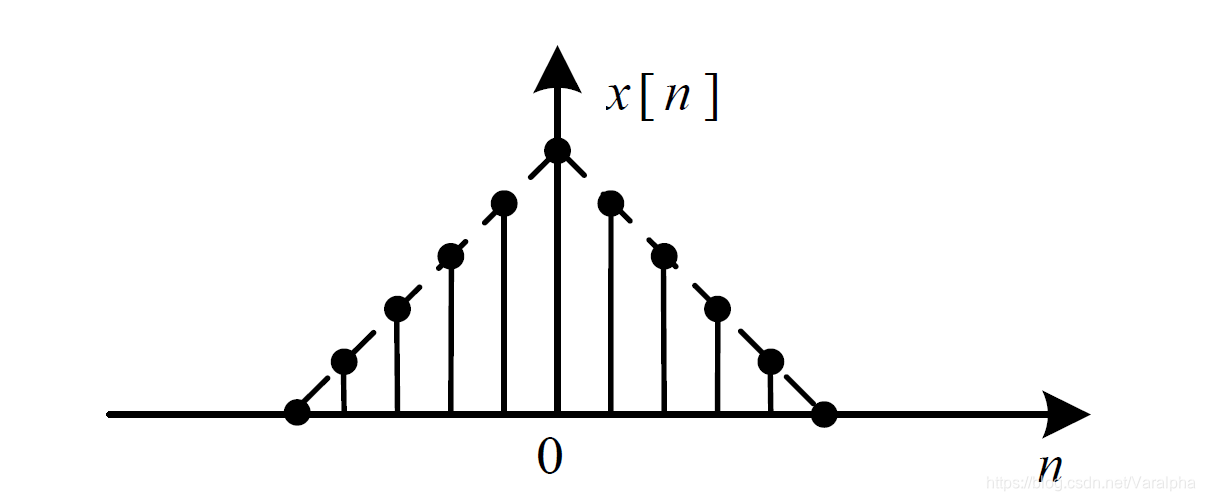
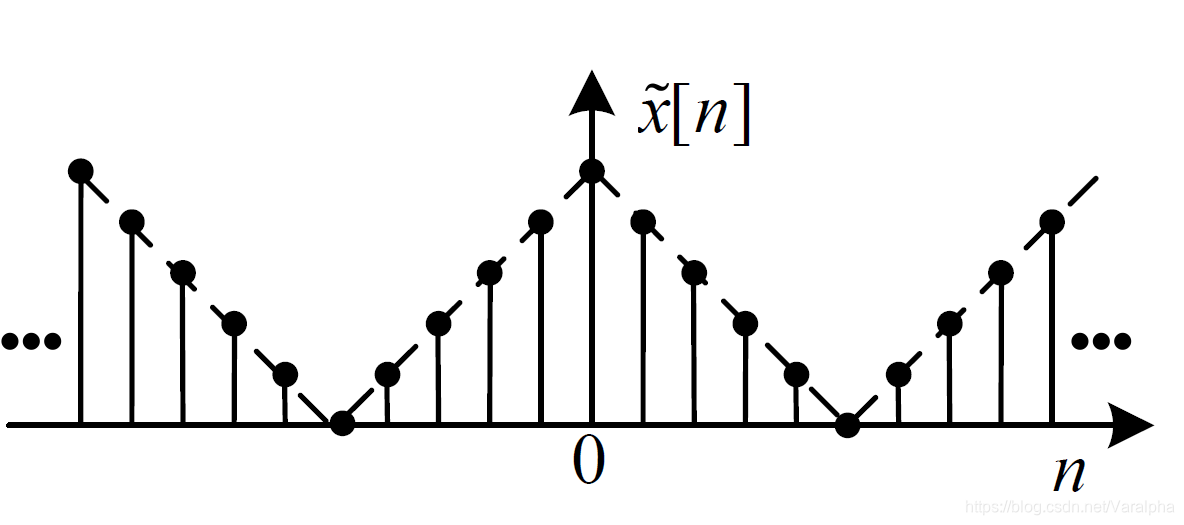
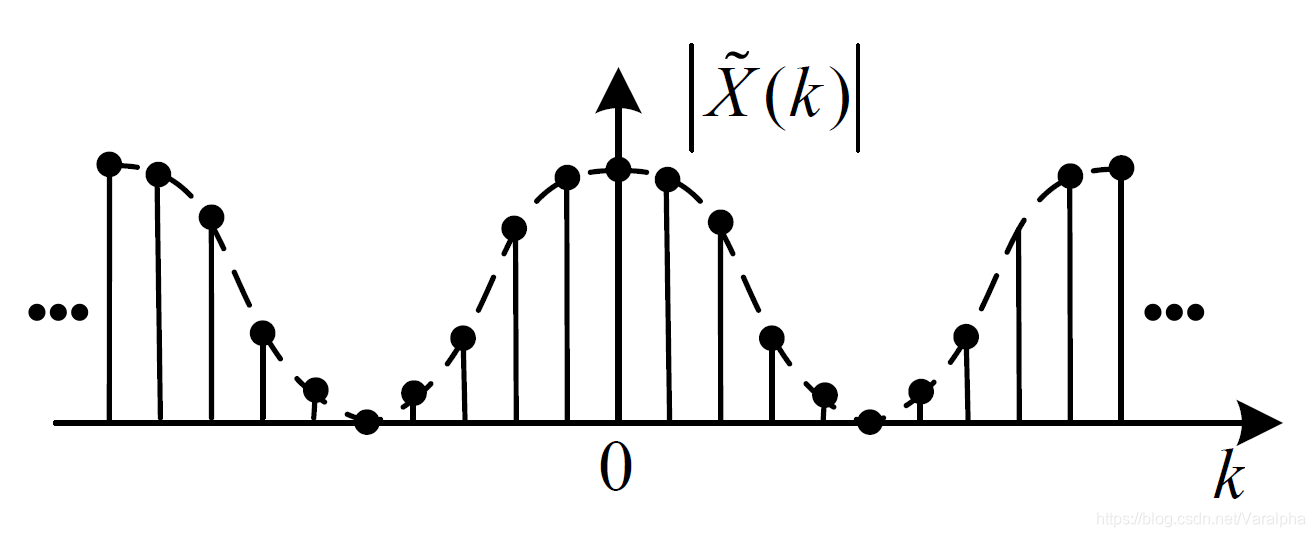
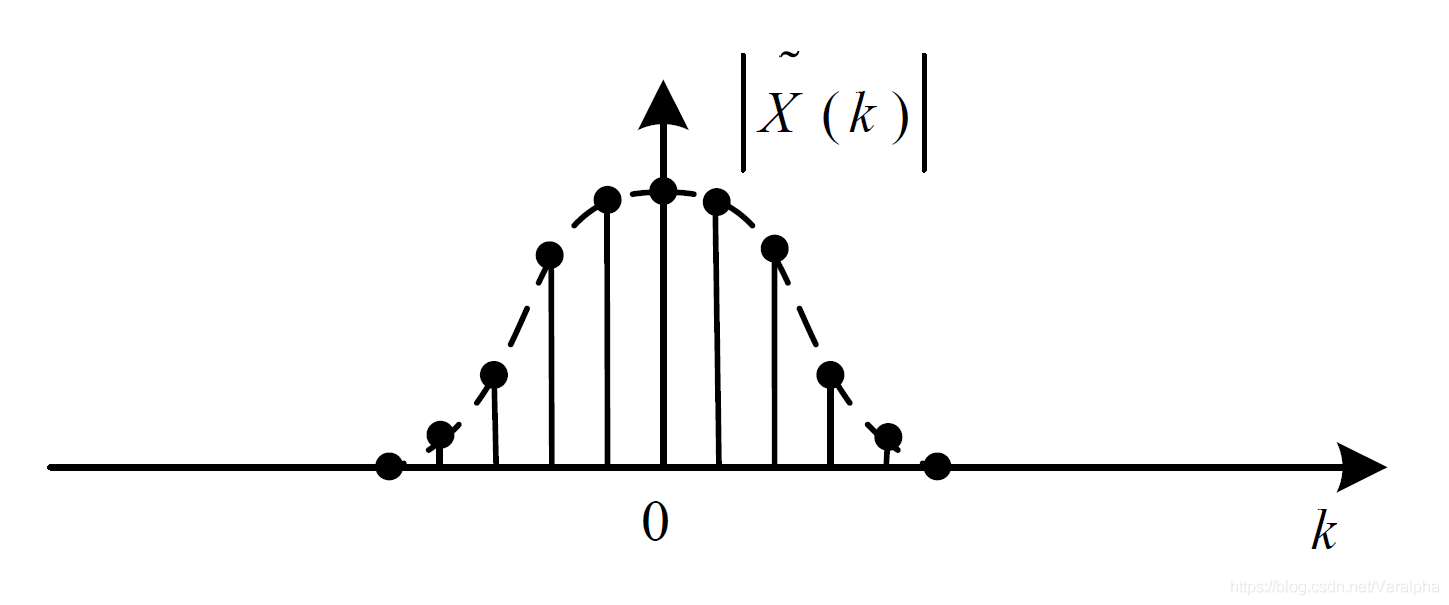
除离散傅里叶变换外,若某个信号在时域(或频域)内是周期的,则经变换 (或反变换)后其变换结果在频域(或时域)内是离散的;若信号在时域(或频域)内是离散的,则其变换(或反变换)结果在频域(或时域)内是周期的。
周期性和离散性呈现出对偶关系。
离散傅里叶变换则提供了一种在时域和频域内均是离散的信号变换方法。
F
(
j
ω
)
=
∫
−
∞
∞
f
(
t
)
e
−
j
ω
t
d
t
F(j\omega) = \int^{\infty}_{-\infty} f(t) e^{-j\omega t} dt
F ( j ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t
傅里叶变换式中,不论在时域还是在频域,信号都是连续 的。
但以计算机为代表的数字处理系统只能存储和处理有限长度 的离散数字信号,且无法直接进行连续积分 运算。
所以需要对信号离散化。
由采样定理知,序列可以看作在满足采样定理的条件下对连续信号进行采样得到,则有:
X
(
j
ω
)
=
∑
n
=
−
∞
∞
x
[
n
⋅
Δ
t
]
e
−
j
ω
n
Δ
t
Δ
t
X(j\omega) = \displaystyle \sum^{\infty}_{n=-\infty} x\big[ n\cdot \Delta t\big] e^{-j\omega n \Delta t} \Delta t
X ( j ω ) = n = − ∞ ∑ ∞ x [ n ⋅ Δ t ] e − j ω n Δ t Δ t
离散时间傅里叶变换 (DTFT -Discrete-time Fourier Transform), 将时域间隔单位归一化后
Δ
t
=
1
\Delta t = 1
Δ t = 1
X
(
j
ω
)
=
∑
n
=
−
∞
∞
x
[
n
]
e
−
j
ω
n
X(j\omega) = \displaystyle \sum^{\infty}_{n=-\infty} x\big[ n\big] e^{-j\omega n}
X ( j ω ) = n = − ∞ ∑ ∞ x [ n ] e − j ω n
上式是将连续傅里叶变换中的时域信号进行离散化后得到
分析:DTFT仍未达到便于数字系统处理的目的:
时域序列的长度仍然是无限长 的
信号在频域 仍然是连续 的
对DTFT而言,其频域变换结果是以
2
π
2\pi
2 π
为此,对时限信号在频域内以
2
π
/
N
2\pi/N
2 π / N DFTF 的变换结果进行频域取样
X
[
k
]
=
∑
n
=
0
N
−
1
x
[
n
]
e
−
h
2
π
N
n
k
,
k
=
0
,
⋯
,
N
−
1
X[k] = \displaystyle \sum^{N-1}_{n=0} x[n] e^{-h\frac{2\pi}{N}nk} , \, k =0,\cdots , N-1
X [ k ] = n = 0 ∑ N − 1 x [ n ] e − h N 2 π n k , k = 0 , ⋯ , N − 1
上式在频域内也是离散且有限的,这非常适合于计算机等数字信号处理系统来进行处理。
该式实际上给出的是非周期离散序列的 离散傅里叶变换 (DFT - Discrete Fourier Transform)。
对周期为
T
T
T
x
(
t
)
x(t)
x ( t )
X
(
j
k
Ω
)
=
1
T
∫
0
T
x
~
(
t
)
e
−
j
k
Ω
t
d
t
\displaystyle X(jk\Omega) = \frac{1}{T}\int^{T}_{0}\tilde{x}(t) e^{-jk\Omega t}dt
X ( j k Ω ) = T 1 ∫ 0 T x ~ ( t ) e − j k Ω t d t
其中
Ω
=
2
π
T
\Omega = \frac{2\pi}{T}
Ω = T 2 π
若要将周期信号在时域内进行离散化,只需以恰当 的采样率 进行采样 ,即可得到对应的周期序列。
离散傅里叶级数 (DFS - Discrete Fourier Series):
对周期为
N
N
N
x
(
n
)
x(n)
x ( n )
X
~
(
j
k
Ω
)
=
1
N
∑
n
=
0
N
−
1
x
~
(
n
)
e
−
j
k
Ω
n
\displaystyle \tilde{X}(jk\Omega) = \frac{1}{N}\sum^{N-1}_{n=0} \tilde{x}(n)e^{-jk\Omega n}
X ~ ( j k Ω ) = N 1 n = 0 ∑ N − 1 x ~ ( n ) e − j k Ω n
若离散周期序列
x
~
(
n
)
\tilde{x}(n)
x ~ ( n )
x
(
n
)
x(n)
x ( n )
且将DFS 变换结果中的一个周期取出来,记作
X
(
j
k
Ω
)
X(jk\Omega)
X ( j k Ω )
X
~
(
j
k
Ω
)
=
1
N
∑
n
=
0
N
−
1
x
~
(
n
)
e
−
j
2
π
N
k
n
\displaystyle \tilde{X}(jk\Omega) = \frac{1}{N}\sum^{N-1}_{n=0} \tilde{x}(n)e^{ -j\frac{2\pi}{N}kn}
X ~ ( j k Ω ) = N 1 n = 0 ∑ N − 1 x ~ ( n ) e − j N 2 π k n
上式本质上与离散傅里叶变换 (DFT )相同。由此可见,离散傅里叶变换 (DFT )可以从DTFT 延伸而来,也可以认为是从DFS 演变得到。
需要说明的是,在常见的信号处理应用中,离散傅里叶变换(DFT)占据主导地位。
定义:
:对于一个长度为
N
N
N
x
[
n
]
(
n
=
0
,
⋯
,
K
,
⋯
,
N
−
1
)
x[n] _{(n = 0,\cdots,K,\cdots, N-1)}
x [ n ] ( n = 0 , ⋯ , K , ⋯ , N − 1 ) DFT )为
X
[
k
]
=
∑
n
=
0
N
−
1
x
[
n
]
W
N
n
k
,
(
k
=
0
,
⋯
,
K
,
⋯
,
N
−
1
)
X[k] = \displaystyle \sum^{N-1}_{n=0} x[n] W^{nk}_{N}, \;(k= 0,\cdots,K,\cdots, N-1)
X [ k ] = n = 0 ∑ N − 1 x [ n ] W N n k , ( k = 0 , ⋯ , K , ⋯ , N − 1 )
其中
W
N
=
e
−
j
2
π
N
W_N = e^{-j\frac{2\pi}{N}}
W N = e − j N 2 π
可验证 :
w
k
=
[
1
,
W
N
−
k
,
W
N
−
2
k
,
⋯
,
K
,
⋯
,
W
N
−
(
N
−
1
)
k
]
T
w^k = \big[ 1 ,\; W_N^{-k} ,\; W_N^{-2k},\; \cdots ,\; K ,\; \cdots ,\; W_N^{-(N-1)k} \big]^T
w k = [ 1 , W N − k , W N − 2 k , ⋯ , K , ⋯ , W N − ( N − 1 ) k ] T
N
N
N
C
N
C^N
C N 正交基 , 也是 DFT 的基数。
由于
∥
w
(
k
)
∥
2
=
N
\lVert w^{(k)} \rVert^2 = N
∥ w ( k ) ∥ 2 = N
1
N
\frac{1}{\sqrt{N}}
N
1
由离散傅里叶变换的公式可知,信号在经过变换后的长度不变,但是由于 DFT 的基是复数,所以通常变换系数也为复数,因此可以从幅度和相位两个方面来分析 DFT 的特性。
离散傅里叶反变换 : 若
X
[
k
]
(
k
=
0
,
⋯
,
K
,
⋯
,
N
−
1
)
X[k]_{(k=0,\cdots,K,\cdots, N-1)}
X [ k ] ( k = 0 , ⋯ , K , ⋯ , N − 1 )
N
N
N
x
[
n
]
=
1
N
∑
k
=
0
N
−
1
X
[
k
]
W
N
−
n
k
,
(
n
=
0
,
⋯
,
K
,
⋯
,
N
−
1
)
\displaystyle x[n] = \frac{1}{N} \sum^{N-1}_{k=0} X[k] W_N^{-nk}, \; (n=0,\cdots,K,\cdots, N-1)
x [ n ] = N 1 k = 0 ∑ N − 1 X [ k ] W N − n k , ( n = 0 , ⋯ , K , ⋯ , N − 1 )
为
X
[
k
]
X[k]
X [ k ] 离散傅里叶反变换 (IDFT )
离散傅里叶变换的物理意义 :
离散傅里叶反变换是将一个有限信号
x
[
n
]
x[n]
x [ n ]
N
N
N
X
[
k
]
X[k]
X [ k ]
更直观地,可以将离散傅里叶反换描述为:
设计一组包含
N
N
N
将其中第
k
k
k
2
π
k
N
\displaystyle \frac{2\pi k}{N}
N 2 π k
将其中第
k
k
k
∣
X
[
k
]
∣
N
\displaystyle \frac{\lvert X[k]\rvert}{N}
N ∣ X [ k ] ∣
将其中第
k
k
k
∠
X
[
k
]
\angle X[k]
∠ X [ k ]
同时启动发生器,将它们的输出相加。按照先后顺序,前
N
N
N
x
[
n
]
,
n
=
0
,
⋯
,
K
,
⋯
,
N
−
1
x[n], \; n=0,\cdots , K, \cdots, N-1
x [ n ] , n = 0 , ⋯ , K , ⋯ , N − 1
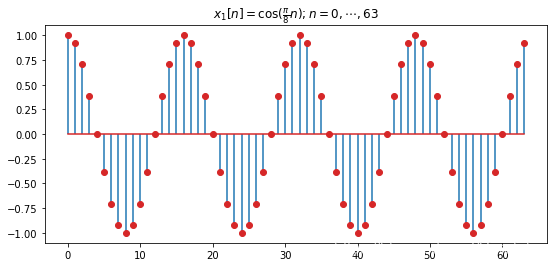
试分析两个信号离散傅里叶变换结果的差异
x
1
[
n
]
=
cos
(
π
8
n
)
,
n
=
0
,
⋯
,
63
x
2
[
n
]
=
cos
(
π
8
n
+
π
3
)
,
n
=
0
,
⋯
,
63
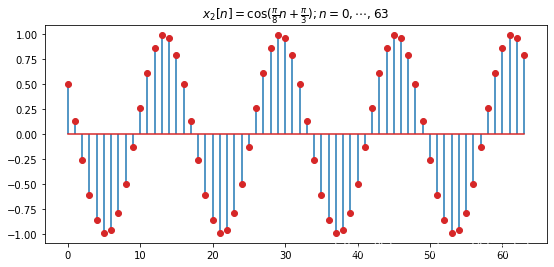
\begin{aligned}x_1[n] & = \cos\Big(\frac{\pi}{8} n\Big), \; & n= 0, \cdots, 63 \\ x_2[n] & = \cos\Big(\frac{\pi}{8} n + \frac{\pi}{3}\Big), \; & n= 0, \cdots, 63\end{aligned}
x 1 [ n ] x 2 [ n ] = cos ( 8 π n ) , = cos ( 8 π n + 3 π ) , n = 0 , ⋯ , 6 3 n = 0 , ⋯ , 6 3
import numpy as np
import matplotlib. pyplot as plt
import scipy. signal as sg
n = np. linspace( 0 , 63 , 64 )
x_1 = np. cos( np. pi/ 8 * n)
x_2 = np. cos( np. pi/ 8 * n+ np. pi/ 3 )
plt. figure( figsize= ( 9 , 4 ) )
plt. title( r'$x_1[n] = \cos(\frac{\pi}{8} n); n= 0, \cdots, 63$' )
plt. stem( n, x_1, '-' , label= 'x_1' , markerfmt= 'C3o' , use_line_collection= True )
plt. show( )
plt. figure( figsize= ( 9 , 4 ) )
plt. title( r'$x_2[n] = \cos(\frac{\pi}{8} n + \frac{\pi}{3}); n= 0, \cdots, 63$' )
plt. stem( n, x_2, '-' , label= 'x_1' , markerfmt= 'C3o' , use_line_collection= True )
plt. show( )
K = np. linspace( 0 , 63 , 64 )
W_64 = np. exp( - 1j * 2 * np. pi / 64 )
X1 = np. array( [ np. sum ( x_1* np. power( W_64, n* k) ) for k in K] )
X2 = np. array( [ np. sum ( x_2* np. power( W_64, n* k) ) for k in K] )
plt. figure( figsize= ( 9 , 4 ) )
plt. rcParams[ 'font.sans-serif' ] = [ 'SimHei' ]
plt. title( r'$x_1[n]$幅度' )
plt. stem( n, X1. real, '-' , label= 'x_1' , markerfmt= 'C3o' , use_line_collection= True )
plt. show( )
plt. figure( figsize= ( 9 , 4 ) )
plt. rcParams[ 'font.sans-serif' ] = [ 'SimHei' ]
plt. title( r'$x_2[n]$幅度' )
plt. stem( n, X2. real, '-' , label= 'x_2' , markerfmt= 'C3o' , use_line_collection= True )
plt. show( )
plt. figure( figsize= ( 9 , 4 ) )
plt. rcParams[ 'font.sans-serif' ] = [ 'SimHei' ]
plt. rcParams[ 'axes.unicode_minus' ] = False
plt. title( r'$x_1[n]$相位' )
plt. stem( n, X1. imag/ 180 * np. pi, '-' , label= 'x_1' , markerfmt= 'C3o' , use_line_collection= True )
plt. ylim( ( - np. pi, np. pi) )
plt. show( )
plt. figure( figsize= ( 9 , 4 ) )
plt. rcParams[ 'font.sans-serif' ] = [ 'SimHei' ]
plt. rcParams[ 'axes.unicode_minus' ] = False
plt. title( r'$x_2[n]$相位' )
plt. stem( n, X2. imag/ 180 * np. pi, '-' , label= 'x_2' , markerfmt= 'C3o' , use_line_collection= True )
plt. ylim( ( - np. pi, np. pi) )
plt. show( )
从上述图可以看出,两个信号的幅频特性相同,但相频特性有明显差异,这与时域表达式中两信号具有相同的角频率但初相不同的结果是一致的。
To TOP 至目录